Преобразования координат

Параллельный перенос.

Поворот вокруг начала координат.

Центральная симметрия. Гомотетия.

Аффинное преобразование.

Рассмотрим ряд преобразований, связанных с переходом из одной системы координат в другую. Здесь (х, у) и (х', у ') - координаты произвольной точки Р соответственно в старой и новой системе координат.

Параллельный перенос. Передвинем систему координат XОY в плоскости так, чтобы оси OX и OY оставались параллельны самим себе, а начало координат О сместилось в точку О' (a, b). Получим новую систему координат X'O'Y' (рис.1):

Координаты точки Р в новой и старой системе координат связаны соотношениями:

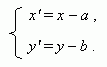
Поворот вокруг начала координат. Повернём систему координат XОY в плоскости на угол (рис.2).

Теперь координаты точки Р в новой и старой системе координат связаны соотношениями:

В частном случае = получим центральную симметрию относительно начала координат О:

Гомотетия с центром О (a, b) и коэффициентом k 0:

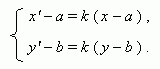
Аффинное преобразование:

Аффинное преобразование переводит прямые в прямые, пересекающиеся прямые – в пересекающиеся прямые, параллельные прямые – в параллельные прямые. Все вышеприведенные преобразования координат являются аффинными.

Прямая

Общее уравнение прямой. Нормальный вектор.

Уравнение прямой с угловым коэффициентом.

Уравнение прямой в отрезках на осях. Уравнение прямой, проходящей

через две различные точки. Параметрическое уравнение прямой.

Условие параллельности прямых. Условие перпендикулярности прямых.

Расстояние между двумя точками. Расстояние от точки до прямой.

Расстояние между параллельными прямыми. Угол между прямыми.

Общее уравнение прямой:

Ах + Ву + С = 0,

где А и В не равны нулю одновременно.

Коэффициенты А и В являются координатами нормального вектора прямой (т.е. вектора, перпендикулярного прямой). При А = 0 прямая параллельна оси ОХ, при В = 0 прямая параллельна оси ОY.

При В 0 получаем уравнение прямой с угловым коэффициентом:

Уравнение прямой, проходящей через точку (х ₀, у ₀) и не параллельной оси OY, имеет вид:

у – у ₀ = m (x – х ₀),

где m – угловой коэффициент, равный тангенсу угла, образованного данной прямой и положительным направлением оси ОХ.

При А 0, В 0 и С 0 получаем уравнение прямой в отрезках на осях:

где a = – C / A, b = – C / B. Эта прямая проходит через точки (a, 0) и (0, b), т.е. отсекает на осях координат отрезки длиной a и b.

Уравнение прямой, проходящей через две различные точки (х ₁, у ₁) и (х ₂, у ₂):

Параметрическое уравнение прямой, проходящей через точку (х ₀, у ₀) ипараллельной направляющему вектору прямой (a, b):

Условие параллельности прямых:

1) для прямых Ах+ Ву+ С = 0 и Dх+ Eу+ F = 0: AE – BD = 0,

2) для прямых у = m x+ k и у = p x+ q: m = p.

Условие перпендикулярности прямых:

1) для прямых Ах+ Ву+ С = 0 и Dх+ Eу+ F = 0: AD + BE = 0,

2) для прямых у = m x+ k и у = p x+ q: m p = – 1.

Расстояние между двумя точками (x ₁, y ₁) и(x ₂, y ₂):

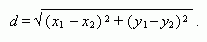
Расстояние от точки (х ₀, у ₀) до прямой Ах+ Ву+ С = 0:

Расстояние между параллельными прямыми Ах+ Ву+ С = 0 и Aх+ Bу+F = 0:

Угол между прямыми:

Окружностью (рис.1) называется геометрическое место точек, равноудалённых от данной точки О, называемой центром окружности, на расстояние R. Число R > 0 называется радиусом окружности.

Уравнение окружности радиуса R с центром в точке О (х ₀, у ₀) имеет вид:

(х – х ₀) ² + (у – у ₀) ² = R ².

Если центр окружности совпадает с началом координат, то уравнение окружности упрощается:

х ² + у ² = R ².

Пусть Р (х ₁, у ₁) – точка окружности (рис.1), тогда уравнение касательной к окружности в данной точке имеет вид:

(х ₁ – х ₀) (х – х ₀) + (у ₁ – у ₀) (у – у ₀) = R ².

Условие касания прямой y = m x + k и окружности х ² + у ² = R ²:

k 2 / (1 + m ² )= R ².

Эллипс

Эллипс. Фокусы. Уравнение эллипса. Фокусное расстояние.

Большая и малая оси эллипса. Эксцентриситет. Уравнение

касательной к эллипсу. Условие касания прямой и эллипса.

Эллипсом (рис.1) называется геометрическое место точек, сумма расстояний от которых до двух заданных точек F ₁ и F ₂, называемых фокусами эллипса, есть величина постоянная.

Уравнение эллипса (рис.1):

Здесь начало координат является центром симметрии эллипса, а оси координат – его осями симметрии. При a > b фокусы эллипса лежат на оси ОХ (рис.1), при a < b фокусы эллипса лежат на оси ОY, а при a = b эллипс становится окружностью (фокусы эллипса в этом случае совпадают с центром окружности). Таким образом, окружность есть частный случай эллипса.

Отрезок F ₁ F ₂ = 2 с, где , называется фокусным расстоянием. Отрезок AB = 2 a называется большой осью эллипса, а отрезок CD = 2 b – малой осьюэллипса. Число e = c / a, e < 1 называется эксцентриситетом эллипса.

Пусть Р (х ₁, у ₁) – точка эллипса, тогда уравнение касательной к эллипсу в данной точке имеет вид:

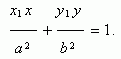
Условие касания прямой y = m x + k и эллипса х ² / a ² + у ² / b ² = 1:

k ² = m ² a ²+ b ².

Гипербола

Гипербола. Фокусы. Уравнение гиперболы. Фокусное расстояние.

Действительная и мнимая оси гиперболы. Эксцентриситет.

Асимптоты гиперболы. Уравнение касательной к гиперболе.

Условие касания прямой и гиперболы.

Гиперболой (рис.1) называется геометрическое место точек, модуль разности расстояний от которых до двух заданных точек F ₁ и F ₂, называемых фокусами гиперболы, есть величина постоянная.

Уравнение гиперболы (рис.1):

Здесь начало координат является центром симметрии гиперболы, а оси координат – её осями симметрии.

Отрезок F ₁ F ₂ = 2 с, где , называется фокусным расстоянием. Отрезок AB = 2 a называется действительной осью гиперболы, а отрезок CD = 2 b – мнимой осьюгиперболы. Число e = c / a, e > 1 называется эксцентриситетомгиперболы. Прямые y = ± (b / a) x называются асимптотами гиперболы.

Пусть Р (х ₁, у ₁) – точка гиперболы, тогда уравнение касательной к гиперболе в данной точке имеет вид:

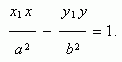
Условие касания прямой y = m x + k и гиперболы х ² / a ² – у ² / b ² = 1:

k ² = m ² a ²– b ².

Парабола

Парабола. Фокус. Директриса. Уравнение параболы.

Уравнение касательной к параболе.

Условие касания прямой и параболы.

Параболой (рис.1) называется геометрическое место точек, равноудалённых от заданной точки F, называемой фокусом параболы, и данной прямой, не проходящей через эту точку и называемой директрисой параболы.

Уравнение параболы (рис.1):

y ² = 2 p x.

Здесь ось ОХ является осью симметрии параболы.

Пусть Р (х ₁, у ₁) – точка параболы, тогда уравнение касательной к параболе в данной точке имеет вид:

у ₁ y = p (x + х ₁).

Условие касания прямой y = m x + k и параболы y ² = 2 p x:

2 m k = p.