Достаточные условия экстремума.

Если производная при переходе через точку x ₀ меняет свой знак с плюса на минус, то x ₀ - точка максимума.

Если производная при переходе через точку x ₀ меняет свой знак с минуса на плюс, то x ₀ - точка минимума.

План исследования функции. Для построения графика функции нужно:

1) найти область определения и область значений функции,

2) установить, является ли функция чётной или нечётной,

3) определить, является ли функция периодической или нет,

4) найти нули функции и её значения при x = 0,

5) найти интервалы знакопостоянства,

6) найти интервалы монотонности,

7) найти точки экстремума и значения функции в этих точках,

8) проанализировать поведение функции вблизи “особых” точек

и при больших значениях модуля x.

П р и м е р. Исследуйте функцию f (x) = x ³ + 2 x ² - x - 2 и постройте график.

Р е ш е н и е. Исследуем функцию по вышеприведенной схеме.

1) область определения x R (x – любое действительноечисло);

область значений y R, так как f (x) – многочлен нечётной

степени;

2) функция f (x) не является ни чётной, ни нечётной

(поясните, пожалуйста);

3) f (x) – непериодическая функция (докажите это сами);

4) график функции пересекается с осью Y в точке (0, – 2),

так как f (0) = - 2; чтобы найти нули функции нужно

решить уравнение: x ³ + 2 x ² - x - 2 = 0, один из корней

которого (x = 1) очевиден. Другие корни находятся

(если они есть!) из решения квадратного уравнения:

x ² + 3 x + 2 = 0, которое получено делением многочлена

x ³ + 2 x ² - x - 2 на двучлен (x – 1). Легко проверить,

что два других корня: x ₂ = -2 и x ₃ = -1. Таким образом,

нулями функции являются: -2, -1 и 1.

5) Это значит, что числовая ось делится этими корнями на

четыре интервала знакопостоянства, внутри которых

функция сохраняет свой знак:

Этот результат может быть получен разложением

многочлена на множители:

x ³ + 2 x ² - x - 2 = (x + 2) (x + 1 (x – 1)

и оценкой знака произведения методом интервалов.

6) Производная f’ (x) = 3 x ² + 4 x -1 не имеет точек, в которых

она не существует, поэтому её область определения R (все

действительные числа); нули f’ (x) – это корни уравнения:

3 x ² + 4 x - 1 = 0.

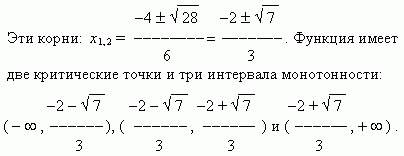
Полученные результаты сведены в таблицу: