Методы интегрирования

Интегрирование по частям.

Интегрирование подстановкой (замена переменной).

Интегрирование по частям. Если функции u (x) и v (x) имеют непрерывные первые производные и существует интеграл v (x) du (x),то существует и интеграл u (x) dv (x) и имеет место равенство:

u (x) dv (x) = u (x) • v (x) – v (x) du (x)

или в более короткой форме:

u dv = u v – v du.

Обратите внимание, что интегрирование по частям и дифференциал произведения являются взаимно обратными операциями (проверьте!).

П р и м е р.	Найти интеграл: ln x dx.
Р е ш е н и е.	Предположим u = ln x и dv = dx, тогда du = dx / x и v = x. Используя формулу интегрирования по частям, получим:

Интегрирование подстановкой (замена переменной). Если функция f (z) определена и имеет первообразную при z Z, а функция z = g (x)имеет непрерывную производную при x X и её область значений g (X) Z, то функция F (x) = f [ g (x)] × g' (x) имеет первообразную на Х и

F (x) dx = f [ g (x)] • g' (x) dx = f (z) dz.

П р и м е р.	Найти интеграл: .
Р е ш е н и е.	Чтобы избавиться от квадратного корня, положим , тогда x = u 2+ 3 и, следовательно, dx = 2 u du. Делая подстановку, имеем:

Некоторые неопределённые интегралы от элементарных функций

В последнем интеграле промежуток интегрирования не содержит x = 0.Ниже мы опускаем постоянную интегрирования C.

Определённый интеграл. Формула Ньютона – Лейбница

Криволинейная трапеция. Определённый интеграл.

Пределы интегрирования. Подынтегральное

выражение. Формула Ньютона – Лейбница.

Рассмотрим непрерывную функцию y = f (x), заданную на отрезке [ a, b ] и сохраняющую на этом отрезке свой знак (рис.8).
Фигура, ограниченная графиком этой функции, отрезком [ a, b ] и прямыми x = a и x = b, называется криволинейной трапецией.
Для вычисления площадей криволинейных трапеций используется следующая теорема:

Если f – непрерывная, неотрицательная функция на отрезке [a, b], и F – её первообразная на этом отрезке, то площадь соответствующей криволинейной трапеции равна приращению первообразной на отрезке [a, b], т.e.

Рассмотрим функцию S (x), заданную на отрезке [ a, b ]. Если a<x b, то S (x) – площадь части криволинейной трапеции, лежащей слева от вертикальной прямой, проходящей через точку (x, 0). Отметим, что если x = a, то S (a) = 0, а S (b) = S (S – площадь всей криволинейной трапеции). Можно доказать, что

т.e. S (x) – первообразная для f (x). Отсюда, согласно основному свойству первообразных, для всех x [ a, b ] имеем:

S (x) = F (x) + C,

где C – некоторая постоянная, F – одна из первообразных функции f.

Чтобы найти C, подставим x = a:

F (a) + C = S (a) = 0,

отсюда, C = - F (a) и S (x) = F (x) - F (a). Так как площадь криволинейной трапеции равна S (b), то подставляя x = b, получим:

S = S (b) = F (b) - F (a).

П р и м е р. Найти площадь фигуры, ограниченной кривой y = x ² и прямыми

y = 0, x = 1, x = 2 (рис.9).

Определённый интеграл. Рассмотрим другой способ вычисления площади криволинейной трапеции. Разделим отрезок [ a, b ] на n отрезков равной длины точками:

x ₀ = a < x ₁< x ₂< x ₃<…< x _{n - 1}< x_n = b

и пусть = (b – a) / n = x_k - x_{k - 1}, где k = 1, 2, …, n – 1, n.

В каждом из отрезков [ x_{k- 1}, x_k ] как на основании построим прямоугольник высотой f (x_{k - 1}). Площадь этого прямоугольника равна:

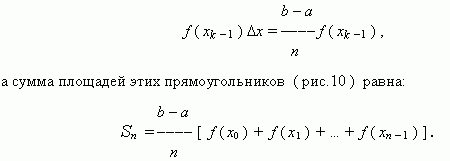
Ввиду непрерывности функции f (x) объединение построенных прямоугольников при большом n (т.e. при малом "почти совпадает" с нашей криволинейной трапецией). Поэтому, S_n S при больших значениях n. Это значит, что S_n S при n 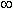. Этот предел называется интегралом функции f (x) от a до b или определённым интегралом:

Числа a и b называются пределами интегрирования, f (x) dx – подынтегральным выражением.

Итак, если f (x) 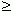0 на отрезке [ a, b ], то площадь S соответствующей криволинейной трапеции вычисляется по формуле:

Формула Ньютона - Лейбница. Сравнивая две формулы для площади криволинейной трапеции, приходим к следующему заключению: если F (x) - первообразная функции f (x) на отрезке [ a, b ], то

Это и есть знаменитая формула Ньютона – Лейбница. Она справедлива для любой функции f (x), непрерывной на отрезке [ a, b ].

Р е ш е н и е. Используя таблицу интегралов элементарных функций

(см. выше), получим:

Основные свойства определённого интеграла

Приложения определённого интеграла в геометрии и механике

Объём тела вращения. Работа переменной силы.

Определённый интеграл имеет многочисленные приложения в математике, механике, физике, астрономии, технике и других областях человеческой деятельности. Мы рассмотрим здесь только два примера,иллюстрирующие возможности этого аппарата.

Объём тела вращения. Рассмотрим тело, полученное вращением вокруг оси OX криволинейной трапеции, ограниченной графиком функции f (x),прямыми x = a и x = b и осью OX (рис.10).

Объём V тела вращения будет равен:

Работа переменной силы. Рассмотрим движение материальной точки вдоль оси OX под действием переменной силы f, зависящей от положения точки x на оси, т.e. силы, являющейся функцией x. Тогда работа A, необходимая

для перемещения материальной точки из позиции x = a в позицию x = b вычисляется по формуле:

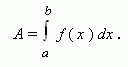
П р и м е р. Найти объём усечённого конуса, образованного вращением

прямой y = x + 1 вокруг оси OX и ограниченной линиями

x = 0 и x = 3.

Р е ш е н и е. В соответствии с вышеприведенной формулой имеем:

Некоторые определённые интегралы