Определенный интеграл как предел интегральной суммы

Пусть функция у = f(x) определена на отрезке [а: b], а < b. Вы­полним следующие действия:

С помощью точек хо = а, Х1, Х2,..., х_п = b (хо < х₁ <... < х_п) разобьем отрезок [а, Ь] на п частичных отрезков [xо; xi], ;[ x_1;x₂],......,[x_n-₁,x_n]

В каждом частичном отрезке [x_i-1;x_i], i — 1,2,...,n выберем произвольную точку Ci Є [х_г-1; х_i] и вычислим значение функции в ней, т. е. величину f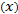

Умножим найденное значение функции f(ci) на длину = = x_i — х_i-1 соответствующего частичного отрезка: f(с_i) •

Составим сумму 5_n всех таких произведений:

S_n = f(c₁) 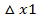+ f(с₂) х₂ +.. - + f(c_n) x_n = (c_i) 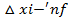Сумма называется интегральной суммой

функции у = f(x) на отрезке [a; b]. Обозначим через λ длину наибольшего частичного отрезка: λ = max

xi (i = 1,2,..., n).

Найдем предел интегральной суммы, когда n 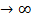так, что λ -> 0.

Если при этом интегральная сумма S_n имеет предел I, который не зависит ни от способа разбиения отрезка [а; b] на частичные отрез­ки, ни от выбора точек в них, то число I называется определенным интегралом от

функции у = f(x) на отрезке [а; b] и обозначается ь

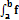(x) dx. Таким образом, 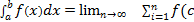_i)

Числа а и b называются соответственно нижним и верхним пределами интегрирования, f(x) подынтегральной функцией, f(x) dx — подынтегральным выражением, х — пере­менной интегрирования, отрезок [а; b] — областью (отрезком)интегрирования. Функция у =f (х), для которой на отрезке [а; b] существует определенный интеграл 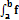(x) dx, называется интегрируемой на этом отрезке.

56.Теорема существования определенного ин­теграла.

Теорема (Коши). Если функция у = f(х) непрерывна на отрезке [a; b], то определенный интеграл 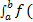x)dx су ществует. Hепрерывность функции является достаточным ус­ловием ее интегрируемости. Однако определенный интеграл может су­ществовать и для некоторых разрывных функций, в частности для вся­кой ограниченной на отрезке функции, имеющей на нем конечное число точек разрыва. Укажем некоторые свойства определенного интеграла, непосред­ственно вытекающие из его определения (35.2). 1. Определенный интеграл не зависит от обозначения переменной интегрирования: 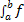(x)dx = 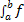(t)dt = 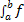(z)dz. Это следует из того, что интегральная сумма (35.1), а следователь-- но, и ее предел (35.2) не зависят от того, какой буквой обозначается аргумент данной функции. 2. Определенный интеграл с одинаковыми пределами интегриро­вания равен нулю: 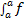(x)dx = 0.3. Для любого действительного числа с: dx = с • (Ь — a).

57. Геометрический смысл определенного интеграла: ( начертить график ) Пусть на отрезке [а; b] задана непрерывная функция у = f(x) ≥ 0. Фигура, ограниченная сверху графиком функции у = f(х), снизу – осью Ох, сбоку – прямыми х = а и х = b, называется криволинейной трапецией. Найдем площадь этой трапеции. Для этого отрезок [а; b] точками а = x0, x1, …, b = xn (x0 < x1 < … < xn) разобьем на n частичных отрезков [x0; x1], [x1;x2], …, [xn-1; xn] (рис. 2.). В каждом частичном отрезке [xi-1; xi], (i = 1, 2, …, n) возьмем произвольную точку и вычислим значение функции в ней, т. е. f(ci). Умножим значением функции f(ci) на длину Δxi = xi - xi-1 соответствующего частичного отрезка. Произведение f(ci) ⋅ Δxi равно площади прямоугольника с основанием Δxi и высотой (ci).

Date: 2016-01-20; view: 572; Нарушение авторских прав