Свойства сравнений

1. отношение сравнений является отношением эквивалентности.

А) Рефлексивность aºа (mod m), т.к. (а-а): m.

Б) Симметричность. Пусть aºb (mod m) => (a-b): m => -(a-b)=b-a: m => bºa (mod m).

В) Транзитивность. Пусть aºb (mod m); bºc (mod m) => (a-b): m; (b-c): m => (a-b) + (b-c)= =(a-c): m; aºc (mod m).

2. сравнение по одному и тому же модулю можно почленно складывать и вычитать.

Пусть aºb (mod m) и cºd (mod m). Покажем, что a+cºb+d (mod m) и a-сºb-d (mod m). Рассмотрим разность (a+c)-(b-d)=(a-b)+(c-d): m, т.к. оба слагаемых кратны m. (a-c)-(b-d)=(a-b)-(c-d): m.

3. к обеим частям сравнения можно прибавлять одно и тоже целое число. Если aºb (mod m), то для "с Î Z; a+cºb+c (mod m); (a+c)-(b-c): m.

Следствие: слагаемое из одной части сравнения можно переносить в другую, меняя при этом знак.

Если aºb+с (mod m), то a-сºb (mod m). Для доказательства к обеим частям сравнения +(-с).

4. сравнение по одному и тому же модулю можно почленно перемножать.

aºb (mod m); cºd (mod m). Покажем, acºbd (mod m).

Док-тво: aºb (mod m) => (a-b): m => (a-b)=mt => a=b+mt; аналогично c=d+mq; ac= (b+mt)·(d+mq)=bd+dmt+bmq+m²tq=bd+m·(bq+dt+mtq) => (ac-bd): m.

Сл: обе части сравнения можно возводить в одну и ту же степень.

1. обе части сравнения можно делить на число, взаимнопростое с модулем.

aºb (mod m); a=a₁d; b=b₁d; (d; m)=1. Покажем a₁ºb₁ (mod m).

Док-тво: aºb (mod m) => (a-b): m => a₁d-b₁d=(a₁-b₁)·d: m; по свойству взаимопростых чисел => (a₁-b₁): m.

1. если aºb (mod m) и m: n, то aºb (mod n).

2. Обе части сравнения и модуль можно умножать на одно и тоже число. Если aºb (mod m), то akºbk (mod mk).

3. Обе части сравнения и модуль можно делить на их общий делитель.

4. Если aºb (mod m₁), aºb (mod m₂), …, aºb (mod m_t), то aºb (mod НОК (m₁, m₂,…,m_t)).

4) Классы вычетов:

Опр: т.к. отношение сравнения по mod m является отношением эквивалентности, множество Z м.б. разбито на классы, называемые классами вычетами.

"a Î Z; Z_a={bÎZ| bºa (mod m)}

m=3: Z₁={1,4,7,10,…,-2,-5,-8,…}; Z₂={2,5,8,…,-1,-4,-7,…}; Z₀={3,6,9,…,0,-3,-6,…}. По модулю 3 разбиение построено.

В один класс входят числа, имеющие одинаковые остатки при делении на m.

По mod m классов вычетов будет ровно столько, сколько различных остатков при делении на m, т.е. m - штук: Z₀, Z₁, …, Z_m-1.

Опр: каждое число в классе вычетов называют вычетом.

В классах принято выделять наименьший положительный или абсолютно наименьшие вычеты.

Пр: m=5, Z₄={5n+4}={4,9,14,…,-1,-6,…}; 4 - наименьший положительный вычет. (-1) - абсолютно наименьший вычет.

Введем на множестве классов вычетов операции. Z_k+Z_m=Z_k+m; Z_k*Z_m=Z_k*m.

Пр: m=6, Z₂+Z₃=Z₅; Z₂*Z₃=Z₆=Z₀.

5) определение полной системы.

Множество классов вычетов образуют кольцо.

Рассмотрим кольцо классов вычетов по mod m, Z/m={Z₀, Z₁,…, Z_m-1}. Выбрав из каждого класса по 1 числу, получим ряд чисел, называемой полной системой вычетов.

Пр: m=5. Z/5={Z₀, Z₁, Z₂, Z₃, Z₄}; -15, 21, 42, -2, 14 - полная система вычетов.

Полную систему вычетов м. выбирать бесконечным числом способов, но чаще рассматривают наименьшие неотрицательные или абсолютно наименьшие.

0; 1; 2; 3; 4 - наименьшие неотрицательные.

0; 1; 2; -2; -1 - абсолютно наименьшие.

Свойства полной системы вычетов:

А) "m попарно несравнимых по mod m чисел образуют полную систему вычетов.

Б) Если x₁, x₂, …, x_m - полная система вычетов по mod m и (k, m)=1, то "b Î Z числа kx₁+b, kx₂+b, …, kx_m+b также образуют полную систему вычетов по mod m.

6) Приведенная система вычетов:

Z/m={Z₀, Z₁, …, Z_m-1}. Выберем по 1 числу из тех классов вычетов, представители которых взамнопросты с m, т.е. из обратимых классов. Полученный ряд чисел называется приведенной системой вычетов.

Пр: Z/6={Z₀, Z₁, Z₂, Z₃, Z₄, Z₅}; Z₁, Z₅ - обратимые классы. 7, 11 - приведенная система вычетов.

Ранее была определена функция Эйлера j(n). Она задавала количество чисел, не превышающих m и взаимнопростых с m. Т.о. приведенная система вычетов содержит j(m) чисел.

Св-ва приведенной системы вычетов:

1. "j(m) попарнонесравнимых м/у собой по mod m и взаимопростых с m чисел образуют приведенную систему вычетов по mod m.

2. Если x₁, x₂, …, x_j(m) - приведенная система вычетов по mod m и (k, m)=1, то kx₁, kx₂,…, kx_j(m) - приведенная система вычетов по mod m.

7) Теорема Эйлера и Ферма:

j(m) - количество натуральных чисел, меньших m и взаимно простых с m.

Пр: j(4)=2; 1, 2, 3, 4.

j(6)=2; 1, 2, 3, 4, 5, 6. j(10)=4.

Теорема Эйлера: Если (a, m)=1, то a^j(m) º 1(mod m).

Док-тво:

x₁, x₂, …, x_j(m) - приведенная система вычетов по mod m. Т.к. (а, m)=1, то по свойству 2 пр. сист. выч.: аx₁, аx₂,…, аx_j(m) - также является приведенной системой вычетов по mod m. Это означает, что "ах_i $ x_j Î одному и тому же классу, т.е. ax_iºx_j (mod m). Т.о. получаем: ax₁ºx_i1(mod m); ax₂ºx_i2(mod m); …; аx_j(m) º x_ij(m) (mod m). Перемножив эти сравнения получаем: a^j(m) x_1*…._* x_j(m)º x_i1x_i2… x_ij(m) (mod m); x₁…. x_j(m) = x_i … x_ij(m), т.к. это те же числа, взятые м.б. в другом порядке.

Покажем, что (x₁…. x_j(m); m)=1. Это следует из того, что x₁…. x_j(m) взяты из приведенной системы вычетов, т.е. (х_i; m)=1, i=1, …, j(m).

Поделив сравнения на x₁…. x_j(m); получим a^j(m) º 1(mod m).

Т. Ферма: (частный случай Т. Эйлера).

Если m=p - простое число и 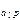, то а^р-1 º 1 (mod p).

Док-тво: следует из Т. Эйлера, т.к. j(р)=р-1.

8) Решение сравнений I степени.

axºb (mod m)

Т1: если (a, m)=1, то сравнение axºb (mod m) имеет единственное решение.

Т2: если (a, m)=d¹1 и 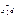, то axºb (mod m) решений не имеет.

Т3: если (a, m)=d¹1 и b: d, то сравнение имеет d - различных решений, которые образуют класс вычетов по mod (m/d).

Способы решения сравнений I - степени:

1. Подбор.

Z₀, Z₁, …, Z_m-1 - ищем среди них решения. Чаще подбор осуществляется другим способом: к правой части сравнения добавляется число, кратное модулю т.о., чтобы полученная сумма делилась нацело на коэффициент.

Пр: 1) 5хº2 (mod 7); 5хº30 (mod 7); хº6 (mod 7)

2) 6хº8 (mod 11); 6хº30 (mod 11); хº5 (mod 11).

2. Способ Эйлера.

Основан на применении теоремы Эйлера: axºb (mod m); (a, m)=1.

По теореме Эйлера: a^j(m) º 1(mod m) | *b; a^j(m) bº b(mod m); a(a^{j(m) -1} b)º b(mod m); a^{j(m) -1}b=x; x º a^{j(m) -1}b (mod m).

3. С помощью цепных дробей.

axºb (mod m) => ax-b=mt => ax-mt=b. Задача сводится к решению неопределенного уравнения в целых числах.

Пр.: 7xº3 (mod 11):

1 сп. 7xº3+11 (mod 11); xº2 (mod 11); Z₂ - решение, Z₂={11k+2}.

2 сп. 7 ^j(11) º1 (mod 11); 7¹⁰º1 (mod 11) | *3; 7(7⁹*3)º3 (mod 11); xº7⁹*3 (mod 11).

3 сп. 7x-3=11t; 7x-11t=3; 7/11=[0; 1, 1, 1, 3].

7*3-11*2=-1 | * (-3); 7*(-9)-11*(-6)=3; xº -9 (mod 11); xº2 (mod 11).