
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Числовые характеристики случайной величины
1. МО (мат-кое ожидание). Пусть случ велич-на имеет возможные значен-я X: x1,…,xn с соответствующими вероятностями p1,…,pn. Опр: МО случ. вел. – это сумма произведен. всех ее возм. знач-й на их вероятность. Если конечное число значений, то М(Х)=х1*р1+…+ хn*рn. Если мн-во знач-й счетно, то М(Х)=åxipi, причем этот ряд сход-ся абсолютно, чтобы его сумма не зависела от порядка расположения членов. Пусть непрерывная случайная величина задана плотностью вероятности f(x). Опр: МО непрер. случ. велич. – интеграл.  . Несобственный интеграл должен сход-ся абсолютно. Вероятностный смысл: МО» равно среднему арифмет-му наблюдаемых знач-й случ. величины (тем точнее, чем больше число испытаний).
. Несобственный интеграл должен сход-ся абсолютно. Вероятностный смысл: МО» равно среднему арифмет-му наблюдаемых знач-й случ. величины (тем точнее, чем больше число испытаний).
Пр.: в результате наблюдения за 2-мя учениками установлено, что они получат оценки с вероятностями.
| Х | |||
| р | 0,3 | 0,4 | 0,3 |
| Y | |||||
| p | 0.1 | 0.1 | 0.1 | 0.2 | 0.5 |
M(X)=3*0.3+4*0.4+5*0.3=4
M(Y)=Yi*pi=3.9; M(X)>M(Y) => X - лучше.
Свойства: 1. М(с)=с, c-const. 2. M(X+Y)=M(X)+M(Y). 3. M(X*Y)=M(X)*M(Y). Сл1. M(cX)=cM(X); Сл2. M(X-Y)=M(X)-M(Y).
2. Пусть заданы две случайные величины X и Y.
| Х | -1 | |
| р | 0,5 | 0,5 |
| Y | -100 | |
| p | 0,5 | 0,5 |
M(X)=0; M(Y)=0; хотя М(Х)=M(Y) эти случайные величины существенно различны. Возможные значения первой близки к ее МО. Возможные значения второй сильно отличаются от ее МО.
Пр: в 2-х учреждениях м.б. одинаковая средняя зарплата, но в 1-ом зарплата сотрудников» одинакова, а во 2-м есть высокооплачиваемые и низкооплачиваемые. Появляется необходимость в такой характеристике случайной величины, которая описывала бы степень разброса, рассеяния возможных значений вокруг МО.
Дисперсия случ. величины – это МО квадрата отклонения случайной величины от ее МО.
D(Х)=М[X-M(X)]2. Для дискретной случайной величины:
 .
.
Для непрерывной случайной величины:
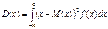
На практике пользуются другой формулой: D(X)=M[x2-2X*M(X)+(M(X))2] = M(X2)-M(2X*M(X))+M[(M(X))2] = M(X2)-2M(X)*M(X)+(M(X))2 = M(X2)-[M(X)]2.
Свойства:
10 D(с)=0. с- const; док-тво: D(с)=М(с2)-М2(с)=с2-с2=0
20 D(сХ)=с2D(Х)
30 D(Х+Y)=D(X)+D(Y), если x,y - независимы.
Следствие: D(Х-Y)=D(X+Y)
3. СКО
Дисперсия имеет недостаток, она имеет размерность квадрата случ. величины. Поэтому с учетом того, что D(x)³0, вводят другую характеристику: СКО. Опр: СКО – это квадратный корень из её дисперсии.
D(Х)=M(X2)-M2(X). 
Из предыдущего примера:  ;
; 
Свойство СКО.
10 s(с)=0, с - const;
20 s(сX)=|c|s(X).
4) Функция распределения.
Задание закона распределения сл. вел. перечислением ее возм. значений исп. только для дискр. сл. вел. Такое задание невозможно для непр. сл. вел., т.к. множество ее значений не счетно. Опр: функцией распределения случ. величины наз. функция, ставящая в соответствие каждому значению х вероятность того, что случ. вел. Х примет значение, меньшее х.  . Геометрически – попадание Х левее х на прямой. Ф-я распределения дискретной случ. вел. есть ступенчатая линия с точками разрыва в точках возможных значений.
. Геометрически – попадание Х левее х на прямой. Ф-я распределения дискретной случ. вел. есть ступенчатая линия с точками разрыва в точках возможных значений.
Опр: Непрерывной случ. вел. наз-тся случ. величина, функция распределения которой непрерывна.
С-ва: 10 0£F(x)£1; 20 F(x) – неубывающая ф-я, т.е. если x1<x2, F(x1)£F(x2). Доказат-во: P(X< x1)+P(x1<=X< x2)=P(X< x2)
 (1)
(1)
Сл.1: Вероятность того, что случайная величина попадет в промежуток [a,b) выражается: P(a£X<b)=F(b)-F(a).
Сл.2: Вер. того, что непрерывная случ. вел. примет одно определенное значение равна нолю, т.е. P(X=x0)=0. Док-тво: из (1): P(x0£X<x0+Dx)=F(x0+Dx)-F(x0). Устремим Dx к нолю.
P(X=x0)=lim Dx®0DF(x0)=0 (т.к. ф-я непрерывна, ее предел=0).
Сл.3: Для непрерывной случ. вел. справедливы равенства:
P(a£X<b)=P(a<X<b)=P(a<X£b)=P(a£X£b). Доказат: P(a£X<b)= P(a<X<b)+P(X=a)= P(a<X<b), т.к. a=0.
30 Если все возможные значения сл. вел. принадл. интервалу [a,b), то а) F(x)=0 при x£a. б) F(x)=1 при x³b. Доказательство из геометрич. смысла: (нарисуй прямую и две точки) F(x1)=P(X<x1)=0, F(x2)=P(X<x2)=1. Сл: 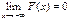 ,
,
(в пределе невозм. событие);  , (в пределе достоверное событие).
, (в пределе достоверное событие).
5) Плотность вероятности.
Пусть дана непрерывная случ. величина Х, ф-я расп. к-рой F(x) имеет непр. производную. Опр: плотностью вероятности непрерывной случ. величины Х наз. производная ее функции распределения, т.е. f(x)=F/(x). Т: Вероятность того, что непр. случ. вел. примет значение, принадл. (a,b) определяется рав-вом:

Д-во:.

График плотности вер-ти наз. кривой распределения. Вер. попадания сл. вел. в интервал (a,b)=площ. фигуры, ограниченной кривой распределения, осью Ох и прямыми х=a, х=b. Плотность вер-ти показ-ет как часто случ вел-на попадает в окр-ть точки при повтор-и опыта.
Сл: 
Док-тво: 
Св-ва: 1) f(x)³0 т.к. f(x) – производная неотрицательная, т.к. F(x) – неубывающая ф-ия. 2) 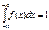 ,
,
Доказательство:  геометрически это значит, что площадь всей фигуры, закл. м/у кривой распред-я и осью Ох=1
геометрически это значит, что площадь всей фигуры, закл. м/у кривой распред-я и осью Ох=1
6) Нормальное распределение.
Непрер-я случ. вел-на подчин-ся норм-у з-ну распр-я, если ее плотность вер-ти им. вид:  , s>0 и a- пар-ры норм распред. График f(x) наз. нормальной кривой или кривой Гаусса. Для построения графика функции исследуем f(x). Исследуем ф-цию.
, s>0 и a- пар-ры норм распред. График f(x) наз. нормальной кривой или кривой Гаусса. Для построения графика функции исследуем f(x). Исследуем ф-цию.
1°. D(y)=R 2°. f(x)>0, 3°  , Ох - является горизонтальной асимптотой. 4° находим производную от f(x). f ' (x)=0 при x=a 5° находим вторую производную: f '' (x)=0; x=a±s 6°.т.к. ф-ция
, Ох - является горизонтальной асимптотой. 4° находим производную от f(x). f ' (x)=0 при x=a 5° находим вторую производную: f '' (x)=0; x=a±s 6°.т.к. ф-ция  - четная, то график ее симметричен относительно Oy.
- четная, то график ее симметричен относительно Oy.
Найдем вероятность попадания нормально расп. сл. вел. в (a,b).

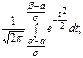
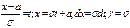

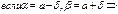

Частный случай: d=3s
P(|X-a|<3s)=2Ф(3)=0.99 Т.к. вероятность близка к 1, то можно считать практически достоверным, что нормально распределенная случ. величина не выходит за пределы интервала (a-3s,a+3s). Это “правило трех сигм”.
7) примеры нормального распределения.
Нормальное распределение очень часто встречается в природе. Нормально распределенными, например, являются такие случайные величины: ошибки при измерении, отклонение при стрельбе, рост людей, размер груди, …
Такое широкое распространение связано с тем, что нормальный закон является предельным для многих других законов, например, для биномиального.
Можно доказать, что сумма очень большого числа случайных величин, влияние каждой из которых на всю сумму ничтожно мало, имеет распределение близкое к нормальному.
Date: 2016-02-19; view: 525; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |