Изоморфные системы (системы с твердыми растворами)

Твердыми растворами называют однородные системы переменного состава, состоящие из двух и более компонентов.

Различают твердые растворы двух типов: внедрения и замещения.

В твердых растворах внедрения атомы (молекулы или ионы) одного компонента размещаются между узлами кристаллической решетки другого компонента. Растворы внедрения получаются при растворении в металлах неметаллов – бора, углерода и т.д.

В твердых растворах замещения частицы (атомы или ионы) одного компонента замещают в узлах кристаллической решетки частицы другого компонента. При этом тип решетки и число атомов сохраняется, но изменяются ее объем и плотность. Частицы двух изоморфных компонентов замещают друг друга в узлах кристаллической решетки совершенно хаотично. Однако, чтобы такой раствор образовался, требуется аналогия химического строения компонентов, такое равенство знаков зарядов ионов, близости радиусов ионов, сходство структур кристаллических решеток. Твердые растворы могут получаться как из химических соединений (например, K₂SO₄ и Rb₂SO₄; KMnO₄ и KCIO₃), так и из простых веществ (например, Cu и Au; Ag и Pt). Продукт совместной кристаллизации изоморфных веществ называется смешанным кристаллом.

Будучи гомогенной фазой, состав которой зависит от состава расплава, смешанный кристалл одновременно является твердым раствором.

Для изоморфных систем диаграмма состояния имеет вид (рис. 8).

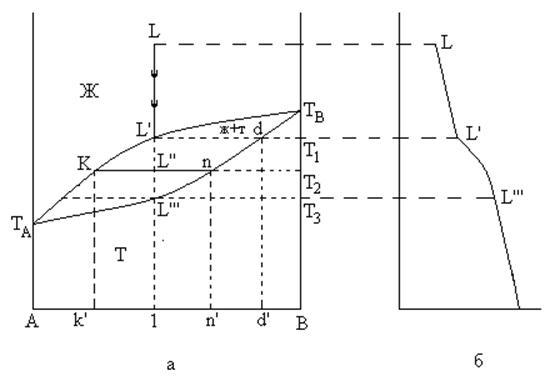
Рис 8. Диаграмма состояния изоморфной системы

Кривая T_AKL’T_B называется ликвидусом. Точки на этой кривой соответствуют началу кристаллизации. Выше кривой ликвидуса при любой температуре и концентрациях, система будет находится в жидком состоянии – расплав компонентов A и B. Отсюда, К_Н = 2, Ф = 1. Число степеней свободы С = 2 + 1 – 1 = 2, система бивариантна.

Кривая T_AL’’’ndT_B называется солидусом. Точки на этой кривой соответствуют концу кристаллизации. Ниже ее система существует только в виде одной твердой фазы, которая представляет собой непрерывный ряд твердых растворов компонентов А и В. Отсюда, К_Н = 2, Ф = 1. Число степеней свободы С = 2 + 1 – 1 = 2, система бивариантна.

Кривые ликвидуса и солидуса сходятся в точках Т_А и Т_В, которые являются температурами плавления компонентов А и В.

Между кривыми ликвидуса и солидуса расположено поле Ж+Т, в пределах которого система состоит из двух фаз: жидкого расплава и твердой фазы – смешанные кристаллы А и В. Эта система моновариантна: К_Н = 2, Ф = 2, тогда С = К_Н +1 – Ф = 2 + 1 – 2 = 1, поэтому любой произвольно выбранной температуре соответствуют вполне определенные составы жидкого расплава и твердой фазы – смешанных кристаллов.

Состав жидкой фазы находят на кривой ликвидуса, состав твердой фазы – на кривой солидуса.

Для диаграммы состояния изоморфных систем характерен плавный, без изломов ход кривых ликвидуса и солидуса. Такой вид кривой ликвидуса означает, что в процессе изменения состояния системы не должно появляться никаких новых фаз, кроме уже образовавшихся. Так как на диаграмме состояния нет точек, в которых в равновесии находилось бы три фазы, и число степеней свободы было бы равно нулю, то на кривой охлаждения LL’L’’’ нет горизонтальных участков.

Действительно, при охлаждении расплава любой концентрации кристаллизуется лишь одна фаза – твердый раствор, состав которого определяется составом равновесной с ним жидкой фазы.

Рассмотрим этот процесс. Пусть имеется смесь компонентов состава 1. Рассмотрим охлаждение расплава обозначенного фигуративной точкой L.

При температуре Т₁ в точке L’ начинается кристаллизация твердого раствора и образуется двухфазная система, состоящая из расплава состава 1 в равновесии с твердым раствором состава d. В интервале температур от Т₁ до Т₃ число степеней свободы равно 1 (С = 2 + 1 – 2 = 1). Каждой температуре соответствуют определенные составы жидкого и твердого растворов. Например, охладить рассматриваемую систему до температуры Т₂ (точка L’’). Тогда она будет состоять из двух фаз.

Для определения их состава проведем через точку L’’ изотерму (ноду), пересечение которой с линией ликвидуса (т. К) даст состав жидкой фазы (К’), а с линией солидуса (т. n) определит состав твердой фазы (т. n’).

Применяя правило рычага можно определить массу твердой и жидкой фазы.

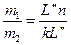
где m₀ – общая масса системы;

m₁ – масса расплава (жидкой фазы);

m₂ – масса кристаллов (твердой фазы);

L’’n и kL’’ – длины отрезков на ноде.

Полное затвердевание расплава произойдет при L’’’ температуре Т₃. При этом состав твердого раствора будет соответствовать составу исходного расплава (1).

Пример 1. По кривым охлаждениядля системы золото – платина построить диаграмму состав – свойство и определить:

1) при какой температуре начнет отвердевать расплав, содержащий 75% Pt;

2) при какой температуре расплав затвердеет полностью;

3) состав первых выпавших кристаллов;

4) количество золота и платины в твердом и жидком состоянии при охлаждении 1,5 кг системы, содержащей 60% Au и 40% Pt;

5) состав последней капли жидкости.

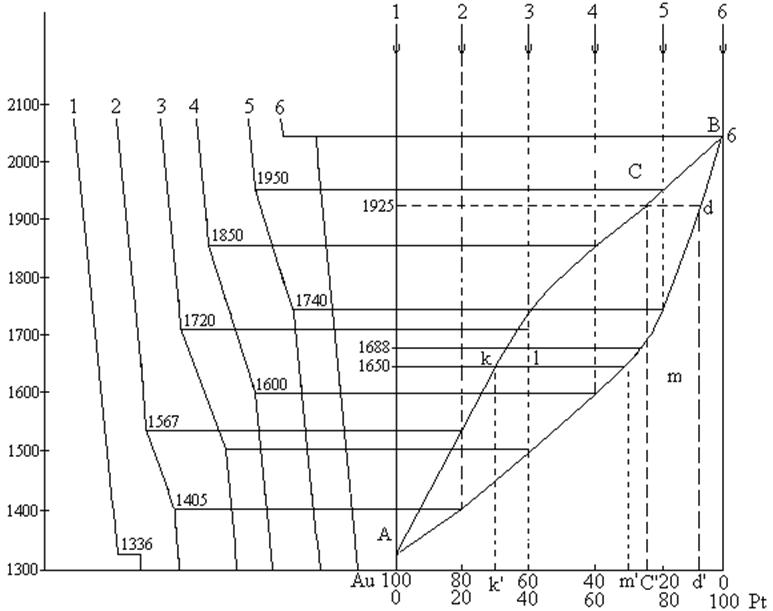
Рис 9.

Решение.

На основании кривых охлаждения строим диаграмму плавкости.

Кривая 1 соответствует охлаждению чистого золота. При Т = 1337К на кривой наблюдается температурная остановка. Она соответствует температуре плавления Au. Чистые вещества кристаллизуются при постоянной температуре, пока жидкая фаза не превратится в твердую. На оси ординат откладываем точку (1337) соответствующую температуре плавления Au.

Кривая 2 соответствует охлаждению системы состоящей из 20% Pt и 80% Au. При Т = 1567К наблюдается на кривой охлаждения некоторый излом (скорость охлаждения уменьшается). Это объясняется выделением теплоты при кристаллизации смеси. При Т = 1405К заканчивается кристаллизация. Тепло больше не выделяется, поэтому некоторый излом на кривой 2 при этой температуре говорит о некотором увеличении скорости охлаждения (идет просто охлаждение полученной твердой системы). На оси ординат соответствующей составу 20% Pt и 80% Au откладываем Т = 1567К (температуру начала кристаллизации). и Т = 1405К (температуру конца кристаллизации). Аналогично находим точки, отвечающим другим составам. Соединив эти точки, получим две кривые АксВ – линия ликвидуса и AmdB – линия солидуса, сходящиеся в точках плавления чистых веществ – диаграмма изоморфной двухкомпонентной системы. Выше линии ликвидуса вся система находится в жидком состоянии (Ф = 1, С = 2), ниже солидуса – в твердом состоянии (Ф = 1, С = 2). Между кривыми АксВ и AmdB часть системы находится в жидком состоянии, а часть перешла в твердое состояние (Ф = 2, С = 1) – область равновесного сосуществования жидких и твердых растворов. Количество веществ, находящихся и жидком и твердом состоянии определяется по правилу рычага.

1. Кристаллизация системы содержащей 75% Pt и 25% Au С’ при Т = 1925К.

2) Кристаллизация закончится, когда состав твердой фазы будет равен составу исходной жидкой фазы, т.е при 1688К.

3) Состав первого кристалла определяется по точке пересечения изотермы начала кристаллизации с линией солидуса (d’).

4) Система, содержащая 40% Pt и 60% Au при охлаждении до 1650К гетерогенна – состоит из жидкой фазы состава К’ и кристаллов состава m’. Массу кристаллов и жидкой фазы определяем по правилу рычага: вес твердой фазы относится к весу жидкой фазы как плечо kl относится к плечу lm, т.е.

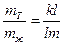
Общий вес смеси 1,5 кг, и если принять, что Х – масса твердой фазы (кристаллов), то (1,5 - Х) – масса жидкой фазы. Измерив длину плеч kl и lm, определим Х

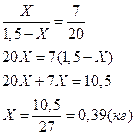
Следовательно, при Т = 1650К выпадет 0,39 кг кристаллов, содержащих 70% Pt и 30% Au (m’) и остается 1,5 – 0,39 = 1,11 кг жидкой фазы состава 30% Pt и 70% Au (k’).

В твердой фазе (кристаллов) содержится 0,39×0,7 = 0,273 (кг) Pt и 0,39×0,3 = 0,117 (кг) Au.

Состав жидкой фазы: Pt 1,11×0,3 = 0,333 кг

Au 1,11×0,7 = 0,777 кг

5) Состав последней капли жидкости находим по пересечению изотермы с линией ликвидуса (к). Последняя капля содержит 30% Pt и 70% Au (k’).

Пример 2.

Воспользовавшись диаграммой плавкости системы Fe – V определить:

1) число степеней свободы системы в точках а, в, с, d;

2) указать в каких пределах изменяется состав жидкого и твердого растворов при затвердевании 60%-ного сплава;

3) ответить на вопрос: определяется ли заданием состава твердого раствора, состава жидкого расплава и температура, при которой эти растворы находятся в равновесии. Находится ли ответ в согласии с правилом фаз?

4) Какая часть 85-ного расплава затвердеет, если его охладить до 1675^оС?

5) сколько ванадия перейдет в твердую фазу, если 15 кг 85%-ного расплава охладить до 1675⁰С?

6) Сколько железа перейдет в жидкую фазу, если 500 г 15%-ного расплава нагреть до 1475⁰С?

Решение.

1) В точке А система состоит из 2 фаз и 2 компонентов. Следовательно, число степеней свободы С = 2 + 1 – 2 = 1, система одновариантна. Точка В изображает состояние однофазной системы. Число степеней свободы С = 2 + 1 – 1 = 2, система бивариантна. В точке С система имеет 2 фазы. но обе фазы имеют одинаковый состав, т.е. система ведет себя как однокомпонентная и число степеней свободы С = 1 + 1 - 2 = 0, система безвариантна.

2) При кристаллизации любого сплава состав жидкой фпзы изменяется по линии ликвидуса, а состав твердой – по солидуса.

Кристаллизация 60%-ного сплава начинается при 1550⁰С, а заканчивается при 1405⁰С. При этом состав жидкого раствора изменяется от 60% до 48%, состав твердого от 72 до 60% V.

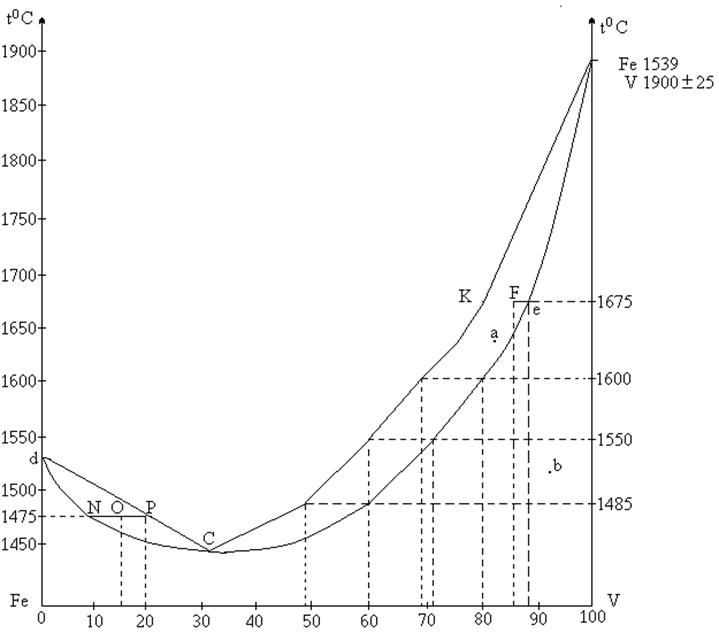
Рис 10.

3) Пусть твердый раствор содержит 80% объема. По диаграмме видно, что этот твердый раствор может находится в равновесии с 69%-ным жидким раствором и только при Т = 1600. Таким образом задавая состав твердого раствора, мы определяем и состав жидкой фазы и температуру, что согласуется с правилом фаз Гиббса, т.к. К_Н = 2, Ф = 2, С = 2 + 1 – 2 = 1, система моновариантна, что означает, что состояние системы определяется заданием одной переменной.

4) Обозначив m_T – твердая фаза, а m_ж – жидкая фаза, а K_f, f_E – плечи рычага. Из диаграммы и правила рычага записываем

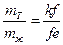
Замеряем линейкой плечи рычага: k_f = 7, f_e = 4

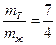
Приняв массу всей системы за 1

m_T + m_Ж = 1.

Исключим m_Ж

m_Ж = 1 - m_T.

тогда

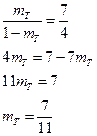
Вывод: при охлаждении 85%-ного сплава до 1675⁰С затвердеет 7/11 частей его.

5) Воспользуемся правилом рычага (см. 4)

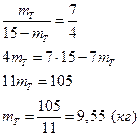
При охлаждении 15 кг 85%-ной до 1675⁰С выделится 9,55 кг твердого сплава, состав которого определяется по диаграмме (т.е.). Он состоит из 88% V. Количество твердого сплава 9,55 кг, следовательно, в нем содержится 9,55×0,88 = 8,40 кг ванадия.

6) Если нагреть 15%-ный сплав до 1475⁰С, то из диаграммы видно, что половина его перейдет в жидкое состояние (NO = OP), т.е. 250 г. В этом сплаве содержится (см. диаграмму, т. Р) 80% Fe. Таким образом, количество железа, перешедшего в жидкую фазу будет равно 250×0,8 = 200 (г).

Уравнение Шредера

Рассмотрим равновесие А_КР «А_А.

Мольная доля вещества в растворе А_{В Р-РЕ} отвечает концентрации насыщенного раствора.

Мольная доля компонента А в кристаллах равна 1. Тогда константа равновесия К = Х_А.

Согласно изобары Вант-Гоффа константа равновесия К зависит от температуры

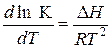
тогда 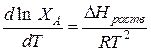(1)

Тепловой эффект растворения (DН_раств) можно определить, представив процесс растворения протекающим в две стадии.

Стадия 1. В начале вещество (А_КР «А_Ж) переходит в одинаковое с растворителем агрегатное состояние, т.е. плавится. Тепловой эффект этого процесса – теплота плавления DН_пл.

Стадия 2. Затем происходит смешение двух жидких веществ. Выделяется теплота смешения - DН_см.

Тогда по закону Гесса DН_раств = DН_пл + DН_см.

Обычно DН_см много меньше DН_пл (DН_пл>>DН_см), а при образовании идеальных растворов равна 0.

Поэтому в уравнении (1) вместо DН_раств можно подставить DН_пл.

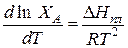(2)

Полученное соотношение называется уравнением Шредера, который вывел его из уравнения Клапейрона–Клаузиуса и закона Рауля.

Если известны температуры кристаллизации двух растворов разного состава, то с помощью (2) можно рассчитать теплоту плавления кристаллизующегося вещества.

Обычно в качестве одной жидкости берут чистое вещество, а в качестве другого – раствор, содержащий небольшое количество другого вещества. Тогда из уравнения (2)

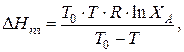
где DН_пл – теплота плавления кристаллизующегося вещества;

Т₀ – температура плавления чистого вещества А;

Т – температура плавления раствора, содержащего кроме А небольшое количество другого вещества;

Х_А – мольная доля вещества А в растворе.

Задание

1. На листе миллиметровой бумаги построить по кривым охлаждения диаграмму состояния в координатах температура – состав.

2. Дать название полученной диаграмме.

3. Охарактеризовать её.

4. Рассчитать криоскопическую константу обоих веществ по формуле

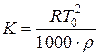
где Т₀ – температура кристаллизации чистого вещества;

r - удельная теплота плавления ;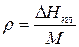

М – молярная масса (г/моль).