
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Реакции n-го порядка
Как мы уже знаем, сложные реакции типа 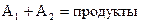 могут протекать по n-му порядку, при этом n может быть целым или дробным числом. Скорость реакции n-го порядка при равных начальных концентрациях реагирующих веществ выражается уравнением:
могут протекать по n-му порядку, при этом n может быть целым или дробным числом. Скорость реакции n-го порядка при равных начальных концентрациях реагирующих веществ выражается уравнением:
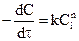
Разделив переменные, получаем:
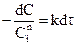 .
.
Интегрируя данное выражение в пределах от 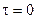 до τ, и от С0 до Сτ, получаем
до τ, и от С0 до Сτ, получаем
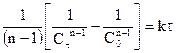 .
.
Данное уравнение можно представить относительно Сτ, что позволяет рассчитать концентрацию реагента в любой момент времени, если известны k и n:
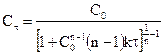 .
.
Уравнение для времени половинного превращения можно получить, как и ранее, приняв, что 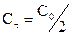 :
:
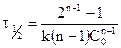 .
.
Представленные уравнения можно использовать для реакций n-го порядка (кроме первого!).
| n | Кинетическое уравнение | Вид зависимости 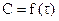
| Уравнения для расчета | |
| k | 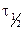
| |||
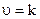
| 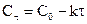
| 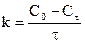
| 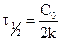
| |
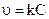
| 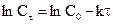
| 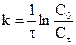
| 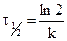
| |
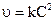
| 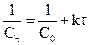
| 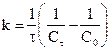
| 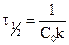
| |
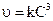
| 
| 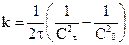
| 
|
определение порядка реакции
Для определения порядка реакции используются различные методы.
Метод подстановки (аналитический): заключается в подстановке экспериментальных данных в уравнения кинетики реакции нулевого, первого, второго и третьего порядков и определении, которое из этих уравнений приводит к постоянному значению константы скорости реакции (можно считать, что уравнение описывает процесс, если рассчитанные по нему значения констант колеблются около какой-то средней величины и отклонения от среднего лежат в пределах возможных погрешностей определения). Если ни одно из уравнений не дает такого результата, то реакция является сложной.
Графический метод: заключается в построении графика, выражающего зависимость различных функций концентрации от времени, и определении, для которой из них зависимость выражается прямой линией. Так для реакции первого порядка прямая получается в системе координат 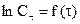 ; для реакции второго порядка
; для реакции второго порядка 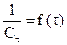 ; для реакции третьего порядка
; для реакции третьего порядка 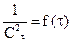 . По тангенсу угла наклона прямой можно определить константу скорости реакции. Для реакции нулевого порядка зависимость концентрации от времени дает прямые, параллельные оси абсцисс.
. По тангенсу угла наклона прямой можно определить константу скорости реакции. Для реакции нулевого порядка зависимость концентрации от времени дает прямые, параллельные оси абсцисс.
Метод определения периода полураспада: основан на определении промежутка времени, в течение которого концентрации (или количества) исходных веществ уменьшаются ровно в два раза. Проводя реакцию при двух различных начальных концентрациях 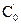 и
и 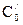 и определяя для обоих случаев периоды полураспада
и определяя для обоих случаев периоды полураспада 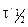 и
и 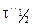 можно определить порядок реакции.
можно определить порядок реакции.
Вспомним уравнение для периода полураспада реакции n-го порядка:
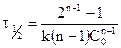 .
.
Получим 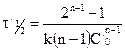 и
и 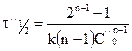 , разделив одно уравнение на другое, получим:
, разделив одно уравнение на другое, получим:
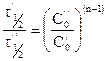 .
.
Откуда
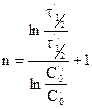
Например, 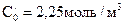 и
и 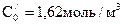 ; периоды полураспада
; периоды полураспада 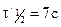 и
и 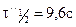 . Определить порядок реакции (n=1,96≈2).
. Определить порядок реакции (n=1,96≈2).
Метод изоляции или метод избытка: реагентов заключается в том, что проводят серии опытов, в каждом из которых изучается влияние изменения концентрации только одного из исходных веществ на скорость реакции. это достигается применением всех остальных исходных веществ в данной серии опытов в таком избытке, что расход их в ходе реакции существенно не меняет их количества (концентрации), которые поэтому можно считать постоянными. Охватывая, таким образом, все исходные вещества, можно установить влияние изменения концентрации каждого из них на скорость реакции и отсюда определить порядок реакции и уравнение кинетики.
Рассмотреть самостоятельно – дифференциальный метод (разновидность графического метода?)!
сложные реакции
Кинетика сложных реакций, состоящих из двух или большего числа простых реакций, в той или иной форме связанных между собой, зависит от формы связи между этими реакциями и от соотношения их скоростей. Типичными по форме такой связи являются реакции:
- параллельные;
- последовательные;
- сопряженные;
- обратимые.
Параллельные: две реакции называются параллельными, если в обеих в качестве исходного вещества выступает одно и то же вещество, т.е. это реакции вида:
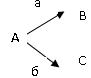
Обозначим, через 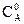 начальную концентрацию вещества А, через х – изменение его концентрации к моменту времени τ, через
начальную концентрацию вещества А, через х – изменение его концентрации к моменту времени τ, через 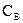 и
и 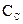 концентрации образовавшихся веществ и через
концентрации образовавшихся веществ и через 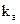 и
и 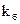 константы скоростей соответствующих реакций. Тогда для скорости образования продуктов реакции имеем:
константы скоростей соответствующих реакций. Тогда для скорости образования продуктов реакции имеем:
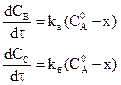 (*)
(*)
Сумма этих скоростей определяет скорость расходования исходных веществ:
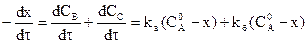 .
.
С другой стороны, отношение этих двух уравнений (*) дает:
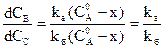 .
.
Таким образом, если в данных условиях термодинамически возможны два или три направления химический реакции, то преобладание того или другого из них и относительные количества получаемых продуктов реакции определяются всецело соотношением скоростей этих реакций, а не соотношением термодинамической устойчивости конечных продуктов. Если реакции значительно различаются по скорости, то обычно реакцию, обладающую большей скоростью, называют главной (основной), а остальные – побочными. При не слишком большом различии в скоростях главной реакцией называют реакцию, приводящую к получению основного нужного продукта, хотя бы она и обладала меньшей скоростью.
Последовательные (или консекутивные): две реакции называются последовательными, если вещество, образующееся в одной стадии, является исходным для другой, т.е. это реакции вида:
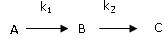 ,
,
где В промежуточный продукт в процессе получения вещества С; k1 и k2 - константы скоростей двух стадий превращения.
Данная схема представляет собой простейшую последовательную реакцию, которая происходит в две ступени, и каждая из этих ступеней является простой мономолекулярной реакцией. В общем же случае ступеней может быть больше, а стадии могут не быть мономолекулярными.
Расчет кинетики последовательных реакций очень сложен. Отметим только, что если одна из ступеней обладает значительно меньшей скоростью, чем остальные, то общая скорость реакции определяется скоростью именно этой реакции!!!
Зависимость концентрации веществ, участников реакции, от времени можно рассмотреть на примере простейшей последовательной реакции:
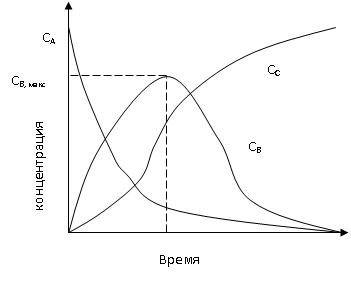
Из данных графических зависимостей следует, что в начале процесса, когда концентрация вещества А еще сравнительно высока, скорость первой реакции значительна и увеличение концентрации В происходит быстро. По мере израсходования вещества А уменьшается и скорость образования вещества В. Это приводит к тому, что расход вещества В на образование вещества С, начиная с какого-то момента времени, уже не компенсируется в полном степени образованием его из вещества А и концентрация вещества В в системе начинает уменьшаться. Вследствие этого кривая Св проходит через максимум. Положение таких кривых для различных последовательных реакций неодинаково, т.к. оно зависит от соотношения в скоростях этих реакций, но общий характер зависимости остается обычно таким, как он рассмотрен нами.
Кривые на рисунке описываются уравнениями:
 ,
,
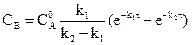 ,
,
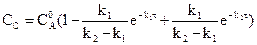 .
.
(реакции первого порядка)
Было доказано, что максимальная концентрация промежуточного продукта В, достигаемая в ходе реакции, не зависит от абсолютных значений констант скоростей k1 и k2, а зависит только от их отношения 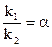 , т.е. чем больше значение α, тем больше должна быть концентрация Св, макс.
, т.е. чем больше значение α, тем больше должна быть концентрация Св, макс.
При k1 > k2 скорость образования промежуточного продукта будет значительно выше скорости его расходования. Таким образом, если промежуточный продукт является целевым и необходимо увеличить его выход, то это может быть достигнуто увеличением k1, что можно достигнуть введением в реакционную систему селективного катализатора, который увеличил бы скорость первой стадии при неизменной скорости второй. Если зависимость скоростей стадий от температуры различна, то тот же эффект может быть достигнут изменением температуры.
При k1 < k2 в этом случае скорость превращения промежуточного вещества В в С будет значительно выше скорости его возникновения из А, а его концентрация будет весьма низкой.
|
из которых одна, например, А+В→М, протекает лишь совместно с другой, т.е. индуцируется последней. В таких случаях вещество С служит индуктором первой реакции (например, окисление сульфата железа и йодистого водорода перекисью водорода. Сульфат железа окисляется независимо от присутствия йодистого водорода, последний же в чистом виде перекисью водорода не окисляется, но при одновременном окислении сульфата железа окисляется совместно с ним). Это явление называется химической индукцией. В этом случае вещество А, общее для обеих реакций называется актором, вещество В – акцептор, а вещество С – индуктор.
Обратимые: скорость обратимой реакции равна разности между скоростями прямой и обратной реакций. Если обратиться к общему случаю реакции вида:
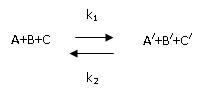
то скорость изменения (убывания) концентрации вещества А при протекании прямой реакции определяется уравнением:
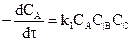
а скорость изменения (возрастания) ее при протекании обратной реакции – уравнением

Если в начальном состоянии системы в ней содержались только вещества А, В, с, то скорость прямой реакции уменьшается по мере течения ее в соответствии с уменьшением этих концентраций. Таким образом, зависимость этой скорости от времени представляется кривой 1, если бы не было обратной реакции, эта кривая достигла бы оси абсцисс при израсходовании одного их исходных компонентов. Кривая 2, относящаяся к скорости обратной реакции, начинается в начале координат (т.к. в начальный момент времени концентрации продуктов реакции равны нулю) и повышается по мере течения прямой реакции и вызываемого ею увеличения этих концентраций.
Общая скорость реакции в любой момент времени равна разности скоростей прямой и обратной реакций:
 .
.
Очевидно, что при дальнейшем течении реакции указанные две кривые – скоростей прямой и обратной реакций – должны где-то пересечься, т.е. должно быть достигнуто такое состояние, при котором скорости прямой и обратной реакций станут равными между собой. После достижения этого состояния – состояния равновесия, концентрации каждого из компонентов реакции будут постоянными.
Так как скорости прямой и обратной реакций при этом будут равны по абсолютному значению, следовательно, должны быть равны между собой и:
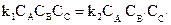 .
.
Откуда
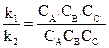 .
.
Правая часть этого равенства представляет собой константу равновесия Кс данной реакции и, следовательно,
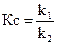 ,
,
т.е. константа равновесия равна отношению констант скоростей прямой и обратной реакций. Этот вывод четко показывает динамический характер равновесия в химических реакциях.

влияние температуры на скорость ХИМИЧЕСКОЙ реакции.
энергия активации
При повышении температуры скорость химической реакции увеличивается; это увеличение весьма значительно. Зависимость скорости протекания реакции от температуры схематично представлена на рисунке.
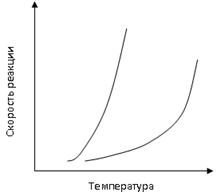 При повышении температуры и постоянных концентрациях реагентов скорость химической реакции увеличивается из-за возрастания константы скорости.
При повышении температуры и постоянных концентрациях реагентов скорость химической реакции увеличивается из-за возрастания константы скорости.
Опытные данные показывают, что если рассматривать зависимость логарифма константы скорости от обратного значения абсолютной температуры, то экспериментальные точки, относящиеся к одной реакции, располагаются обычно практически на одной прямой, т.е. логарифм константы скорости реакции находится в линейной зависимости от обратного значения абсолютной температуры (1/Т). Искомая зависимость выражается уравнением Аррениуса:
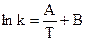 ,
,
где А и В индивидуальные константы, характерные для данной реакции.
Аррениусом было предложено объяснение физического смысла постоянной А в данном уравнении.
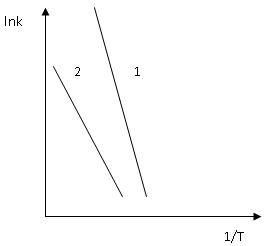 Вспомним уравнение изохоры Вант-Гоффа в дифференциальной форме:
Вспомним уравнение изохоры Вант-Гоффа в дифференциальной форме:
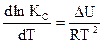 ,
,
которое выражает температурный коэффициент константы равновесия через тепловой эффект химической реакции. Подставляя в это уравнение вместо Кс отношение констант скоростей прямой и обратной реакций 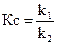 , можно получить:
, можно получить:
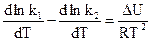 .
.
Вант-Гофф высказал предположение о возможности рассматривать тепловой эффект реакции, как разность двух энергетических величин 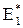 и
и 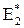 , относящихся к прямой и обратной реакциям, отсюда
, относящихся к прямой и обратной реакциям, отсюда 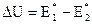 . С учетом данного равенства, уравнение
. С учетом данного равенства, уравнение 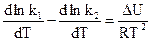 можно разложить на два уравнения вида:
можно разложить на два уравнения вида:
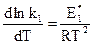 и
и 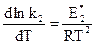 .
.
Интегрируя данные уравнения при постоянстве 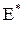 , получаем:
, получаем:
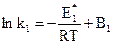 и
и 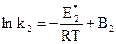 ,
,
где 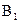 и
и 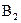 - постоянные интегрирования.
- постоянные интегрирования.
Величины 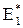 и
и 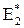 называются энергиями активации. Они связаны с постоянной А уравнения
называются энергиями активации. Они связаны с постоянной А уравнения 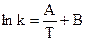 простым соотношением
простым соотношением 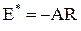 . Согласно представленным уравнениям, константа скорости реакции, а, следовательно, и скорость химической реакции сильнее изменяются с температурой в тех реакциях, в которых энергия активации больше. И наоборот, если в данной реакции энергия активации незначительна, то скорость этой реакции слабо изменяется с температурой. Кроме того, чем больше энергия активации данной реакции, тем при более высоких температурах она совершается.
. Согласно представленным уравнениям, константа скорости реакции, а, следовательно, и скорость химической реакции сильнее изменяются с температурой в тех реакциях, в которых энергия активации больше. И наоборот, если в данной реакции энергия активации незначительна, то скорость этой реакции слабо изменяется с температурой. Кроме того, чем больше энергия активации данной реакции, тем при более высоких температурах она совершается.
Рассмотрим физический смысл энергии активации.
В реакциях, протекающих с конечной скоростью, число столкновений между молекулами, приводящих к химическому взаимодействию (число эффективных столкновений), составляет лишь некоторую часть от общего числа столкновений. Эффективными считаются лишь столкновения между молекулами, которые в момент столкновения обладают некоторым избытком внутренней энергии по сравнению со средней для данной температуры величиной. Именно этот избыток энергии, необходимый молекулам для данной реакции в данных условиях, и представляется энергией активации 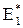 и
и 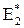 . Энергия активации – это то избыточное количество энергии (по сравнению со средней величиной), которой должна обладать молекула в момент столкновения, чтобы быть способной к данному химическому взаимодействию. Рассмотрим на примере рисунка. На рисунке по вертикальной оси отложена энергия активации рассматриваемой системы молекул, а по горизонтальной – ход реакции. Допустим прямая реакция (переход из состояния 1 в состояние 2) является экзотермической, то общий запас продуктов реакции меньше, чем исходных веществ, т.е. система в результате этой реакции переходит на более низкий энергетический уровень (это также показывает, что повышение температуры всегда сильнее увеличивает скорость эндотермического направления реакции, т.к. энергия активации больше. А также, повышение температуры всегда смещает равновесия в направлении эндотермического процесса и тем в большей степени, чем выше тепловой эффект, т.е. чем больше разница в энергиях активации прямой и обратной реакций). Разность в энергиях этих уровней равна тепловому эффекту реакции ΔН. Уровень К определяет наименьший запас энергии, которым должны обладать молекулы. Чтобы их столкновение было эффективным. Разность между этим уровнем К и уровнем 1 представляет собой энергию активации прямой реакции
. Энергия активации – это то избыточное количество энергии (по сравнению со средней величиной), которой должна обладать молекула в момент столкновения, чтобы быть способной к данному химическому взаимодействию. Рассмотрим на примере рисунка. На рисунке по вертикальной оси отложена энергия активации рассматриваемой системы молекул, а по горизонтальной – ход реакции. Допустим прямая реакция (переход из состояния 1 в состояние 2) является экзотермической, то общий запас продуктов реакции меньше, чем исходных веществ, т.е. система в результате этой реакции переходит на более низкий энергетический уровень (это также показывает, что повышение температуры всегда сильнее увеличивает скорость эндотермического направления реакции, т.к. энергия активации больше. А также, повышение температуры всегда смещает равновесия в направлении эндотермического процесса и тем в большей степени, чем выше тепловой эффект, т.е. чем больше разница в энергиях активации прямой и обратной реакций). Разность в энергиях этих уровней равна тепловому эффекту реакции ΔН. Уровень К определяет наименьший запас энергии, которым должны обладать молекулы. Чтобы их столкновение было эффективным. Разность между этим уровнем К и уровнем 1 представляет собой энергию активации прямой реакции 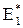 , а разность между уровнями К и 2 – энергию активации обратной реакции
, а разность между уровнями К и 2 – энергию активации обратной реакции 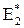 . Таким образом, по пути из исходного состояния в конечное система должна преодолеть так называемый энергетический барьер. Только молекулы, обладающие в момент столкновения необходимым избытком энергии, так называемые активные молекулы, могут вступать в химическое взаимодействие. Катализаторы, ускоряющие реакцию, обычно, тем или иным путем, снижают ее энергию активации и этим увеличивают относительное число активных молекул. Повышение температуры увеличивает среднюю кинетическую энергию, что повышает и относительное число молекул, обладающих энергией, превосходящей энергию уровня К. Избыточная энергия может быть в молекуле в различных формах, это может быть: 1) повышенная кинетическая энергия поступательного или вращательного движения, 2) повышенная энергия взаимного колебания атомов или атомных групп, составляющих молекулу, 3) повышенная энергия движения тех или других электронов. Для различных реакций не все формы этой энергии равноценны.
. Таким образом, по пути из исходного состояния в конечное система должна преодолеть так называемый энергетический барьер. Только молекулы, обладающие в момент столкновения необходимым избытком энергии, так называемые активные молекулы, могут вступать в химическое взаимодействие. Катализаторы, ускоряющие реакцию, обычно, тем или иным путем, снижают ее энергию активации и этим увеличивают относительное число активных молекул. Повышение температуры увеличивает среднюю кинетическую энергию, что повышает и относительное число молекул, обладающих энергией, превосходящей энергию уровня К. Избыточная энергия может быть в молекуле в различных формах, это может быть: 1) повышенная кинетическая энергия поступательного или вращательного движения, 2) повышенная энергия взаимного колебания атомов или атомных групп, составляющих молекулу, 3) повышенная энергия движения тех или других электронов. Для различных реакций не все формы этой энергии равноценны.
расчеты констант скоростей и энергии активации
Для выражения зависимости константы скорости реакции от температуры и определения энергии активации, а также для расчета константы скорости при различных температурах используют уравнение 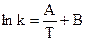 . Две постоянные в данном уравнении могут быть определены, если известны значения констант скорости данной реакции k1 и k2 при двух температурах Т1 и Т2. Имеем систему из двух уравнений:
. Две постоянные в данном уравнении могут быть определены, если известны значения констант скорости данной реакции k1 и k2 при двух температурах Т1 и Т2. Имеем систему из двух уравнений:

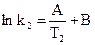
с двумя неизвестными А и В. Вычитая первое уравнение из второго, получим:
 .
.
Это дает возможность непосредственно определить А (а, следовательно, энергию активации, т.к. 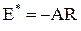 ). Подставляя полученное значение А в одно из уравнений, рассчитывают постоянную В. Полученное уравнение с численными значениями постоянных А и В можно использовать для расчета константы скорости при промежуточных температурах. Существует также графический способ определения энергии активации!
). Подставляя полученное значение А в одно из уравнений, рассчитывают постоянную В. Полученное уравнение с численными значениями постоянных А и В можно использовать для расчета константы скорости при промежуточных температурах. Существует также графический способ определения энергии активации!
Обозначим через 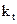 константу скорости при температуре t0С и через
константу скорости при температуре t0С и через 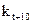 константу скорости той же реакции при температуре (t+10)0С. Отношение
константу скорости той же реакции при температуре (t+10)0С. Отношение 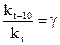 называется температурным коэффициентом скорости. Было предложено приближенное правило, согласно которому повышение температуры на 100С увеличивает скорости реакций примерно в 2-4 раза (правило Вант-Гоффа), т.о.
называется температурным коэффициентом скорости. Было предложено приближенное правило, согласно которому повышение температуры на 100С увеличивает скорости реакций примерно в 2-4 раза (правило Вант-Гоффа), т.о. 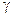 можно принять равным примерно 2-4.
можно принять равным примерно 2-4.
Данное правило определяет только порядок изменения скорости, присущий значительной части различных химических реакций при обычных температурах. Однако для ориентировочной оценки возможного влияния температуры оно нередко бывает полезным, в особенности при отсутствии данных для более точного расчета.
Date: 2015-05-09; view: 5558; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |