Построение изображений

Линзы - прозрачные тела, ограниченные частями сферических поверхностей (частный случай - одна из поверхностей плоская). Световые лучи преломляются на обеих поверхностях линзы и дают изображение “действительное” (получается на пересечении преломленных лучей) или “мнимое” (получается на пересечении продолжения преломленных лучей). Собирающая линза - превращает световой пучок в сходящийся. Рассеивающая линза - превращает световой пучок в расходящийся.

Формула тонкой линзы (толщина линзы много меньше радиусов кривизны поверхностей) ,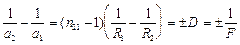

а₁ –расстояние от линзы до предмета, а₂ –расстояние от линзы до изображения, R₁, R₂– радиусы кривизны поверхностей, ограничивающих линзу, 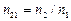– показатель преломления вещества линзы относительно окружающей среды, D–оптическая сила линзы, F–фокусное расстояние линзы.

Правило знаков: все отрезки отсчитывают от границы раздела; по ходу луча отрезки считают положительными, против хода луча – отрицательными. Для собирающей линзы D>0, для рассеивающей – D<0.

Поперечное увеличение линзы: 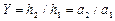, где h₁, h₂ - поперечны размера предмета и изображения.

Увеличение оптической системы: 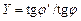, где j¢, j – углы, под которыми рассматривают предмет с помощью прибора и без него.

Примеры решения задач.

Задача 1. Цилиндрический пучок лучей, параллельных главной оптической оси рассеивающей линзы, имеет диаметр d₁ = 5 см. Пройдя линзу, пучок дает на экране пятно диаметром d₂ = 7 см. Каким будет диаметр d₃ пятна, если рассеивающую линзу заменить собирающей с тем же фокусным расстоянием?

Дано: d₁=5 см, d₂=7 см, F₁=F₂=F

Найти: d₃ -?

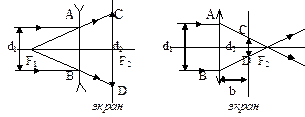
Решение. Лучи, параллельные главной оптической оси, после преломления на рассеивающей линзе идут так, что их продолжение идет через фокус F₁; для собирающей линзы преломленные лучи идут через фокус F₂. Обозначим расстояние от линзы до экрана – b. Тогда из подобия треугольников DABF_1,2 и DCDF_1,2

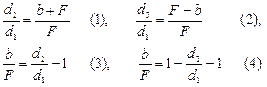
Приравнивая правые части равенств (3) и (4), получаем: 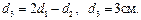Ответ: d₃=3 см.

Задача 2. В куске стекла с показателем преломления n_cт=1,5 имеется воздушная полость в виде двояковыпуклой линзы с радиусами кривизны поверхностей R=10 см. На оптической оси этой линзы внутри куска стекла на расстоянии 20 см от линзы находится песчинка. Определить расстояние между изображением песчинки и линзой.

Дано: n_возд= 1, n_cт =1,5, R₁=R₂=R=10 см, a₁ =20 см

Найти: а₂ –?

Решение. По формуле тонкой линзы

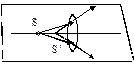
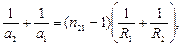
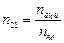– относительный показатель преломления вещества линзы относительно окружающей среды.

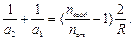
Отсюда 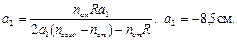Знак (–) означает, что изображение “мнимое”, то есть линза в данном случае рассеивающая. Ответ: а₂ = –85 см.

Задача 3. Оптическая система состоит из собирающей линзы с фокусным расстоянием F и плоского зеркала, расположенного перпендикулярно к главной оптической оси. Расстояние между линзой и зеркалом 4F. Точечный источник света находится на главной оптической оси посредине между линзой и зеркалом. найти расстояние между действительными изображениями источника.

Дано: a₁=a₁’=2F, L=4F

Найти: S₁S₂ –?

Решение. Пучок света от источника S попадает частично на плоское зеркало. Лучи, преломленные на линзе, дают изображение S₁. Лучи. отраженные от зеркала, падают на линзу и, преломляясь, дают изображение S₂. При этом изображение точки S в зеркале S’ является для линзы источником.

По формуле тонкой линзы 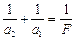. Отсюда 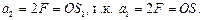По формуле плоского зеркала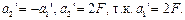

Изображение точки S в плоском зеркале S’ – мнимое.

.

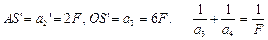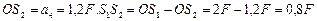
Отсюда 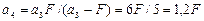Ответ: OS₂=0,8 F.

Задача 4. Зрительная труба с фокусным расстоянием 50 см установлена на бесконечность. После того как окуляр трубы передвинули на некоторое расстояние, стали видны предметы, удаленные от объектива на 50 м. На какое расстояние передвинули окуляр при наводке.

Дано: a₁=¥, a₁’=50 м, F₁= 50 см = 0,5 м.

Найти: D l –?

Решение. Так как вначале объектив зрительной трубы установлен на бесконечность, то есть a₁=¥, то изображение, даваемое объективом, попадает в фокальную плоскость объектива а₂ =F₁. Согласно формуле тонкой линзы 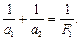Это изображение попадает и в фокальную плоскость окуляра, т.к. задний фокус объектива совпадает с передним фокусом окуляра, играющего роль лупы. Если а₁ ’=50 м, то .

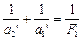Отсюда 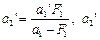=0,505 м=50,5 см. В этом случае изображение, даваемое объективом, сместилось вправо на расстояние

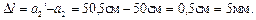
На такое же расстояние следует передвинуть и окуляр зрительной трубы, чтобы изображение попало в фокальную плоскость окуляра. (Указание: ход лучей в зрительной трубе смотрите в теории к данному разделу.)

Задачи для самостоятельного решения.

4.1. Из двух стекол с показателями преломления 1,5 и 1,7 сделаны две одинаковые двояковыпуклые линзы. 1)Найти отношение их фокусных расстояний. 2) Какое действие каждая из этих линз произведет на луч, параллельный оптической оси, если погрузить линзы в прозрачную жидкость с показателем преломления 1,6?

4.2. Линза с фокусным расстояние 16 см дает резкое изображение предмета при двух положениях, расстояние между которыми 60 см. Найти расстояние от предмета до экрана.

4.3. Найти фокусное расстояние линзы, погруженной в воду, если известно, что ее фокусное расстояние в воздухе равно 20 см. Показатель преломления стекла, из которого сделана линза, равен 1,6.

4.4. В фокальной плоскости двояковыпуклой линзы расположено плоское зеркало. Предмет находится перед линзой между фокусом и двойным фокусным расстоянием. Построить изображение предмета.

4.5. На экран с круглым отверстием радиуса 10 см падает сходящийся пучок света. Угол между крайним лучом и осью симметрии равен 30^о. Определите точку. в которой будут сходиться лучи, если в отверстие вставляется: 1) собирающая; 2) рассеивающая линзы. D₁=D₂ =10 диоптрий.

4.6. Сходящийся пучок, проходящий через отверстие диаметром 6 см в непрозрачном экране I, падает на экран II, находящийся за экраном I на расстоянии 50 см, светлое пятно диаметром 3 см. После того как в отверстие I поместили линзу, пятно превратилось в точку. Найти фокусное расстояние линзы.

4.7. Собирающая линза с фокусным расстоянием F=20 см состоит из двух половинок. Определить расстояние между изображениями точечного источника, если половинки раздвинуть: 1) на расстояние d₀=1 см перпендикулярно главной оптической оси; 2) на то же расстояние одна из половинок сдвигается от источника вдоль оптической оси; 3) не раздвигая линзу, закрыть ее среднюю часть непрозрачным экраном диаметром d₀. Источник расположен на расстоянии 75 см от линзы.

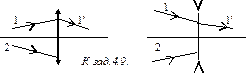4.8. Собирающая и рассеивающая линзы имеют общую оптическую ось. Фокусные расстояния равны соответственно F₁= a, F₂=–b (a > b). Лучи, параллельные оси, после прохождения системы не изменяют направления. Найти расстояние между линзами.

4.9. Найдите построением ход луча 2 после тонкой линзы, если известен ход луча 1.

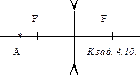4.10. Постройте изображение точки А, находящейся на оптической оси рассеивающей линзы.

4.11. На рисунке показаны положения оптической оси тонкой линзы MN, точки S и ее изображения S’. Найдите построением положение центра тонкой линзы и ее фокусов.

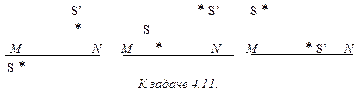
4.12. Световой пучок от источника S, находящегося в фокальной плоскости тонкой линзы, падает на линзы. Показать ход этих лучей после линзы.

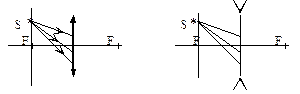
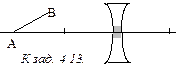4.13. Средняя часть линзы заклеена черной бумагой. Найдите построением изображение предмета АВ.

4.14. Параллельный пучок света падает на линзу, затем на вогнутое зеркало. Фокусное расстояние зеркала равно 24 см. Расстояние между линзой и зеркалом 32 см. Каким должно быть фокусное расстояние линзы, чтобы свет, отразившись от зеркала, собрался в точке, удаленной от зеркала на расстояние 6 см.

4.15. Увеличение микроскопа 600. Определите оптическую силу объектива, если фокусное расстояние окуляра F_ок=4 см, а длина тубуса l= 24см.

4.16. В отверстие в экране вставлена рассеивающая линза с фокусным расстоянием 10см, на которую падает параллельный пучок лучей. На расстоянии 30 см от линзы параллельно ее плоскости расположен экран. При замене рассеивающей линзы на собирающую такого же диаметра радиус светлого пятна на экране не изменился. Чему равно фокусное расстояние собирающей линзы?

4.17. Действительное изображение предмета, полученное с помощью собирающей линзы, находится от нее на расстоянии 8см. Если собирающую линзу заменить рассеивающей с таким же фокусным расстоянием, мнимое изображение этого предмета будет отстоять от линзы на 2см. Найти абсолютную величину фокусного расстояния линз (в мм).

4.18. Два точечных источника света находятся на расстоянии 24см друг от друга. Между ними на расстоянии 6 см от одного из них помещена собирающая линза. При этом изображения обоих источников получились в одной и той же точке. Найдите фокусное расстояние линзы (в см.).

4.19. Вдоль оптической оси собирающей линзы с фокусным расстоянием 5 см расположен стержень так, что его середина находится на расстоянии 8 см от линзы. Чему равна (в см) длина этого стержня, если его продольное увеличение равно 5.

4.20. Тонкий стержень расположен вдоль главной оптической оси собирающей линзы. Каково продольное увеличение стержня, если объект, расположенный у одного конца стержня изображается с увеличением 2,75? Оба конца стержня расположены от линзы на расстоянии больше фокусного.

4.21. На оси тонкой рассеивающей линзы с фокусным расстоянием 5см и диаметром d=2 см на расстоянии 20 см от нее находится точечный источник света. По другую сторону линзы на расстоянии 10 см от нее расположен экран. Найти диаметр D светлого пятна на экране.

4.22. Небольшое тело находится на горизонтальной подставке на оси собирающей линзы с фокусным расстоянием F. Расстояние между линзой и телом равно 2F. Телу сообщают скорость u, направленную от линзы вдоль ее главной оптической оси. Коэффициент трения о подставку равен µ. Какое расстояние пройдет изображение тела в линзе к моменту остановки тела?

4.23. Небольшой шарик, подвешенный на нити длиной l вращается в горизонтальной плоскости вокруг вертикальной оси, проходящей через точку подвеса. Под шариком на расстоянии а от плоскости вращения закреплена тонкая собирающая линза с фокусным расстоянием F (F< а) так, что ее главная оптическая ось совпадает с осью вращения шарика. Найти угловую скорость шарика, если его изображение вращается по окружности радиусом R.

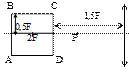4.24. Квадрат со стороной равной фокусному расстоянию тонкой собирающей линзы расположен так, как показано на рисунке. Построить изображение квадрата и найти отношение площадей квадрата и его изображения.

4.25. Точечный источник света находится под поверхностью жидкости на глубине h = 20 см. С помощью тонкой собирающей линзы получают уменьшенное изображение поверхности жидкости на экране, отстоящем от поверхности на расстоянии l =10 см. Фокусное расстояние линзы F=1,6 см. Определить радиус освещенного пятна на экране. Показатель преломления жидкости n=1,5.

4.26. Собирающая линза с оптической силой Д₁=2дптр и рассеивающая линза с оптической силой Д₂=-1,5дптр расположены на расстоянии а =40 см друг от друга и имеют общую оптическую ось. Со стороны собирающей линзы на расстоянии 4м от нее находится предмет высотой h=20см. Определить, где и какое изображение предмета дадут эти линзы. Предмет расположен на оптической оси линзы, параллельно ее плоскости.

4.27. На оси ОХ в точке х₁=0 находится оптический центр тонкой рассеивающей линзы, а в точке х₂=15см – тонкой собирающей линзы с фокусным расстоянием F₂=15см. Главные оптические оси обеих линз лежат на оси ОХ. На рассеивающую линзу падает параллельный пучок света вдоль оси ОХ из области х<0. Пройдя данную оптическую систему, лучи собираются в точке с координатой х₃=45см. Найдите фокусное расстояние рассеивающей линзы F₁.

4.28. На оси ОХ в точке х₁=15см находится оптический центр тонкой рассеивающей линзы с фокусным расстоянием F₁=–15 см, а в точке х₂=27,5см – тонкой собирающей линзы. Главные оптические оси обеих линз совпадают с осью ОХ. Свет от точечного источника, расположенного в точке х=0, пройдя данную оптическую систему, распространяется параллельным пучком. Найдите фокусное расстояние собирающей линзы F₂.

4.29. На оси ОХ в точке х₁=0 находится оптический центр тонкой рассеивающей линзы с фокусным расстоянием F₁=–30см, а в точке х₂=30 см – тонкой собирающей линзы с фокусным расстоянием F₂=30см. Главные оптические оси обеих линз лежат на оси ОХ. На рассеивающую линзу по оси ОХ падает параллельный пучок света из области х<0. Найдите координату х точки (в см), в которой собирается этот пучок, пройдя данную оптическую систему.

4.30. Линза, фокусное расстояние которой 20см дает на экране изображение предмета с 4-х кратным увеличением. Экран подвинули к линзе вдоль ее главной оптической оси на 40см. Затем при неизменном положении линзы передвинули предмет, чтобы изображение снова стало резким. Определите увеличение во втором случае.

4.31. Линза, фокусное расстояние которой 12 см, дает на экране изображение предмета с четырехкратным увеличением. Экран передвинули вдоль главной оптической оси линзы. Затем при неизменном положении линзы передвинули предмет, чтобы изображение снова стало резким. В этом случае получено изображение с трехкратным увеличением. На сколько пришлось сдвинуть предмет относительно его первоначального положения?

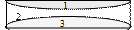4.32. Из плоскопараллельной стеклянной пластинки изготовили 3 линзы, разрезав ее так, как показано на рисунке. Фокусное расстояние линз1 и 2, сложенных вместе равно – F, фокусное расстояние линз 2 и 3 равно – F. Определите фокусное расстояние каждой из линз отдельно.

Date: 2015-05-05; view: 7497; Нарушение авторских прав