Примитивно-рекурсивные функции

Теоретические сведения

Известно, что рекурсия есть способ определения значения функции в некоторой точке через известные значения этой функции в других, предшествующих точках. Очевидно, что в каждой точке должен быть задан набор значений аргументов данной функции, а в некоторой исходной точке – значение самой функции.

В тех случаях, когда речь идет о числовых функциях, области определения и значения которых заданы на множестве целых положительных чисел, это описание рекурсии задает способ вычисления численных значений определяемой функции для заданного набора числовых значений аргументов и числовых значений этой функции в исходной точке.

Числовые функции, для которых существует алгоритм вычисления их значений, называют рекурсивными функциями.

Если числовая функция определена не для всех значений аргументов, ее называют частично рекурсивной функцией. Если для всех значений – то общерекурсивной функцией.

Исследование алгоритмов на множестве рекурсивных функций оправдано тем, что любое вещественное число может быть представлено цепочкой <целое> «.»<целое>, для которой существует только одна синтаксическая переменная – <целое>. Следовательно, любую функцию можно свести к рекурсивной, если значения аргументов и значения функции рассматривать принадлежащими синтаксической переменной <целое>.

Последовательность функциональных равенств, описывающих по шагам дискретный процесс вычисления числовой функции от ее исходного значения при заданных значениях независимых переменных аргумента, называют рекурсивным описанием, или протоколом.

Формализм вычисления является универсальной моделью описания последовательности шагов в реализации алгоритма.

Для этой модели должны быть заданы наборы элементарных объектов и элементарных действий в описании механизма реализации алгоритма. Такими элементарными объектами являются три базовые функции, а элементарными действиями – три элементарные операции.

Простейшие одношаговые рекурсивные функции называются базовыми. К числу таких функций относятся функции константа, тождества и следования.

Функция константа. Если f = {(x₁; x₂;... x_n; у) | x_iÎ X; yÎ Y } = c_n, то любым значениям аргументов функции ставится в соответствие ее значение, равное постоянной величине – c_n, чаще всего нулю.

Например, если f = (x₁; x₂; x₃; у) = c₃, то для x₁ = 5, x₂ = 4, x₃ = 7 и c₃ = 0имеем у = 0; если f = x₁; x₂; x₃; у) = c_з, то для x₁= 5, x₂ = 4, x₃ = 7 и c_з = 1 имеем у = 1.

Функция тождества. Если f = {(x₁; x₂;... x_n; у) | x_iÎ X; yÎ Y }= J_n;m, то любым значениям переменных аргумента функции ставится в соответствие ее значение, равное значению m-го независимого аргумента, где 1£ m £ n – номер выбранного независимого аргумента.

Например, если f = (x₁; x₂;... x_n; у) = j_3,2, то для x₁ = 5, x₂= 4, x₃ = 7 имеем у=4; если f = (x₁; x₂;... x_n; у) = j_3,3, то для x₁= 5, x₂= 4, x₃= 7 имеем у = 7.

Функция следования. Если f = (х; у) = l, то любому значению независимой переменной аргумента функции ставится в соответствие ее значение, равное числу, непосредственно следующиму за числом, являющимся значением независимой аргумента.

Например, если f = (х; у) = l(х), то для х = 5 имеем у = (х+1) = (5+1) = 6; если f = (х; у) = l(х), то для х = 7 имеем у = (х +1) = (7 +1)= 8.

Простейшие операции, с помощью которых из базовых функций могут быть получены рекурсивные функции, называют элементарными.

К числу элементарных операций относят операции суперпозиции, рекурсии и минимизации.

Операция суперпозиции. Если даны функция h от m независимых переменных аргумента, т.е. h = (z₁; z₂;... z_m; у), и m функций q_i от n независимых переменных аргумента, т.е. {q_i=(x_1i; x_2i;... x_ni; z_ij)}, то в результате подстановки функций q₁, q₂... q_m вместо аргументов функции h может быть получена новая функция f=(x₁; x₂;... x_n; у) от n независимых переменных аргумента, т.е.

h = (z₁; z₂:... z_m; y):

q₁ = (x₁; x₂;... x_n; z₁);

q₂ = (x₁; x₂;... x_n; z₂);

...................................

q_m = (x₁; x₂;... x_n; z_m);

h = (q₁; q₂;... q_m; y) = f = (x₁; x₂;... x_n; y).

Значения функций q₁; q₂;... q_n, найденные при заданных значений независимых переменных x₁; x₂;... x_n, принять за значения независимых переменных аргумента функции h и вычислить ее значение, которое принять за значение функции f = (x₁; x₂;... x_n; y).

Например, если h = (z; y) = l(z) и q(х; z) = l(х), то f=(q; у) = l(l) = l²(х). Следовательно, для х = 5 имеем z=5 + 1= = 6 и у = 6 + 1 = 7.

Оператор суперпозиции, реализующий одноименную операцию, часто записывают так:

f = x₁; x₂;... x_n; y = S_mⁿ (h^(m); q₁⁽ⁿ⁾; q₂⁽ⁿ⁾;... q_m⁽ⁿ⁾),

где h^(m) =(z₁; z₂;... z_m; y) и

q₁⁽ⁿ⁾ = (x_1i ⁽ⁿ⁾; x_2i ⁽ⁿ⁾;... x_ni ⁽ⁿ⁾; z_i).

Если заданы функции тождества (I_n,m) и оператор суперпозиции (S_mⁿ), то можно считать заданными всевозможные операторы подстановки, перестановки и переименования любых функций.

Операция рекурсии. Если даны n-местная рекурсивная функция g и (n + 2)-местная рекурсивная функция h, то можно найти (n + 1)-местную рекурсивную функцию f, используя схему примитивной рекурсии:

f (x₁; x₂;... x_n; 0) = g (x₁; x₂;... x_n;);

f (x₁; x₂;... x_n; у+1) = h (x₁; x₂;... x_n; у; f(x₁; x₂;... x_n; у)).

Схема примитивной рекурсии позволяет определить значения функций f не только через значения функций g и h, но и через значения функций f во всех предшествующих точках аргумента.

Схема примитивной рекурсии содержит главный дополнительный аргумент – у, который войдет в значение определяемой функции, и один вспомогательный аргумент – f (x₁; x₂;... x_n; у), который позволяет определить значение искомой функции для последующих значений главного дополнительного аргумента.

Пример 1. Доказать, что функция 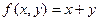является примитивно-рекурсивной.

Решение. Так как данная функция 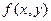есть функция двух аргументов, то для использования операции примитивной рекурсии мы должны иметь функцию g, зависящую от одного аргумента, и функцию h, зависящую от трех аргументов. Определим их.

В функции 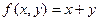положим y =0. Тогда имеем 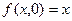- это тождественная функция. Полагая y =1, получим 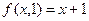- это функция следования.

Таким образом, выбираем следующие элементарные функции: тождественную 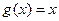и функцию следования 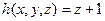. Заметим, что здесь .

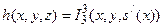Используем схему примитивной рекурсии:

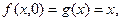
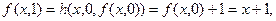
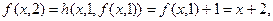
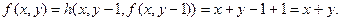
Таким образом, построена функция (таблица ее значений) которая равна сумме двух слагаемых.

Пример 2. Доказать, что функция 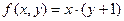является примитивно-рекурсивной.

Решение. Заметим, что

.

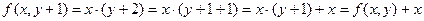Найдем требуемые функции 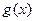и h. Для этого считаем, что, так как заданная функция 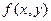есть функция двух аргументов, следует выбрать функцию g, зависящую от одного аргумента, и функцию h, зависящую от трех аргументов.

Для заданной функции модно записать

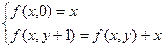
Первая из этих функций – это тождественная функция 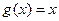, а вторая определяет функцию h. Это функция сложения двух чисел, которая, как доказано выше, является примитивно-рекурсивной. Поэтому можно использовать ее для выбора функции h.

Итак, имеем для операции примитивной рекурсии:

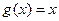- функция одного аргумента,

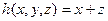- функция трех аргументов.

Проверим, что функции выбраны правильно. Из определения операции примитивной рекурсии имеем:

…………………..

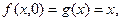
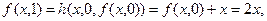
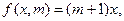
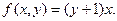
Примитивно-рекурсивность операции умножения доказана. Этот факт можно использовать при доказательстве примитивной рекурсивности других функций.