
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Применение эквивалентных бесконечно малых
Бесконечно малые 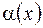 и
и 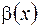 называются эквивалентными при
называются эквивалентными при  , если
, если 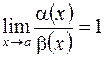 Обозначается эквивалентность так:
Обозначается эквивалентность так: 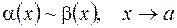 . Применение эквивалентных б.м. является очень эффективным способом раскрытия неопределенностей. В основе следующая теорема.
. Применение эквивалентных б.м. является очень эффективным способом раскрытия неопределенностей. В основе следующая теорема.
Теорема. Пусть функции 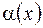 и
и 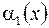 являются эквивалентными при
являются эквивалентными при  . Если существует конечный или бесконечный
. Если существует конечный или бесконечный 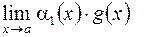 , то существует
, то существует 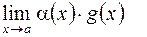 , причем
, причем
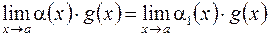 . (3)
. (3)
Из этой теоремы следует, что если при 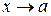
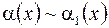 ,
, 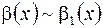 , то
, то 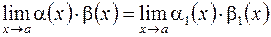 ;
;
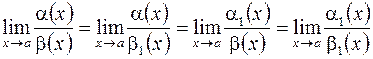 .
.
Эти равенства означают, что при вычислении пределов множители в числителе или в знаменателе можно заменить на эквивалентные
Приведем некоторые пары эквивалентных бесконечно малых величин
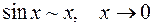 ;
; 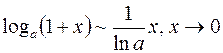 ;
;
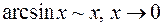 ;
; 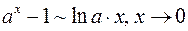 ;
;
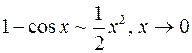 ;
; 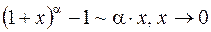 .
.
Пример 1. Вычислить 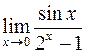 .
.
Решение. Функции 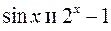 являются б.м. при
являются б.м. при  , заменим их эквивалентными б.м.:
, заменим их эквивалентными б.м.: 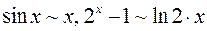 , при
, при  .
.
Тогда
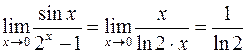 .
.
При помощи замены б.м. на эквивалентную удается очень быстро преодолеть те искусственные, иногда громоздкие преобразования, которые нами использовались при раскрытии неопределенностей другими способами. Чтобы убедиться в этом, вернемся к примеру 3, п.3 и вычислим его с помощью эквивалентных б.м.. При 
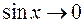 , поэтому
, поэтому 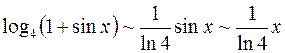 ; бесконечно малая
; бесконечно малая 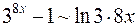 . Тогда
. Тогда
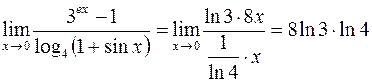 .
.
Преимущества использования бесконечно малых очевидны.
Пример 2. Вычислить 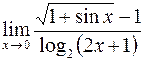 .
.
Решение. Обозначим 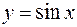 и заметим, что при
и заметим, что при  новая переменная y тоже
новая переменная y тоже 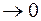 . Тогда
. Тогда 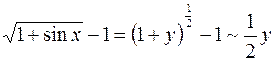 при
при  , т.е.
, т.е. 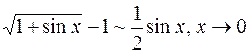 . При
. При  б.м.
б.м. 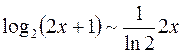 . Тогда
. Тогда
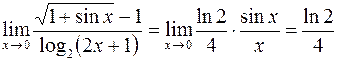 .
.
Метод замены переменной, использованный в данном примере, значительно расширяет возможности применения эквивалентных б.м. величин.
Замечание. Не рекомендуется заменять под знаком предела слагаемые на эквивалентные им величины. Например, при 
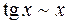 ;
; 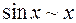 . Если перейти к эквивалентным функциям в примере
. Если перейти к эквивалентным функциям в примере
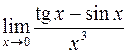 , то получим
, то получим 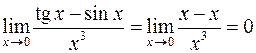 .
.
В действительности все обстоит по-другому:
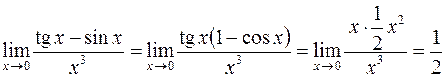 .
.
Рассмотренные примеры связаны с неопределенностью  , но эквивалентные б.м. можно использовать при раскрытии и других неопределенностей.
, но эквивалентные б.м. можно использовать при раскрытии и других неопределенностей.
Пример 3. Вычислить 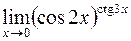 .
.
Решение. Неопределенность 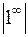 . Применим следующие преобразования:
. Применим следующие преобразования:
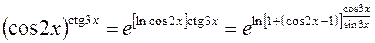 .
.
При  ,
, 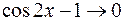 , тогда
, тогда 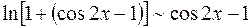 . В свою очередь,
. В свою очередь, 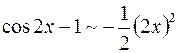 . Поэтому
. Поэтому
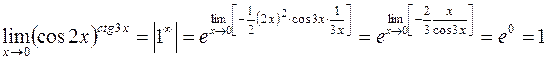 .
.
Пример 4. Вычислить 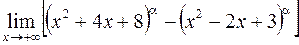 , где
, где 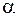 - произвольное положительное число.
- произвольное положительное число.
При 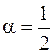 данный предел можно вычислить путем умножения и деления на сопряженное выражение. Для других значений
данный предел можно вычислить путем умножения и деления на сопряженное выражение. Для других значений 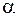 такой метод уже не проходит. Используя эквивалентные б.м. этот предел можно вычислить без особого труда. Сначала применим дополнительные преобразования:
такой метод уже не проходит. Используя эквивалентные б.м. этот предел можно вычислить без особого труда. Сначала применим дополнительные преобразования:
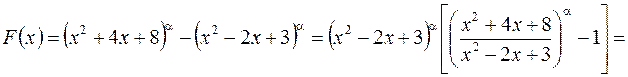
 .
.
Т.к. при 
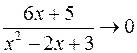 , то
, то 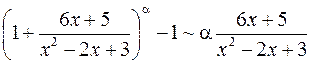 .
.
Тогда 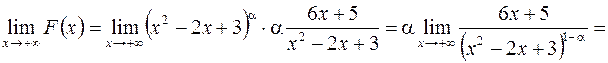
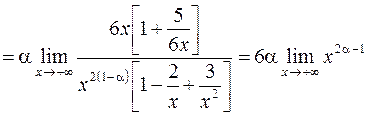 .
.
В зависимости от возможных значений показателя степени функции 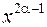 ведет себя по-разному при
ведет себя по-разному при 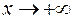 . Если
. Если 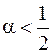 , то
, то 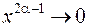 . Тогда искомый предел равен 0. Если
. Тогда искомый предел равен 0. Если 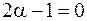 , то он равен
, то он равен 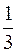 , и наконец, если
, и наконец, если 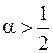 , то
, то 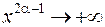 , предел равен
, предел равен 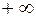 .
.
Date: 2015-12-10; view: 612; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |