Глава 1. Высказывания, формулы, тавтологии

Определение. Высказыванием называется утверждение, которое является истинным или ложным (но не одновременно).

То есть, чтобы выяснить, является ли некоторое предложение высказыванием, нужно сначала убедиться, что это утверждение, а затем установить, истинно оно или ложно.

Пример. “Москва – столица России” – истинное высказывание.

“5 –четное число” – ложное высказывание.

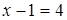“ ” – не высказывание (неизвестно, какие значения принимает ).

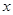“Студент второго курса” не высказывание (не является утверждением).

Высказывания бывают элементарные и составные.

Элементарные высказывания не могут быть выражены через другие высказывания. Составные высказывания можно выразить с помощью элементарных высказываний.

Пример. “Число 22 четное” – элементарное высказывание.

“Число 22 четное и делится на 11” – составное высказывание.

Высказывания обозначают заглавными буквами латинского алфавита: , , 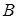,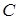… Эти буквы называют логическими атомами.

При фиксированном множестве букв 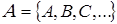интерпретацией называется функция 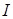, которая отображает множество 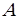во множество истинностных (логических) значений 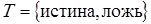, то есть .

Истинностные значения истина и ложь сокращенно обозначаются и, л или T, F, или 1,0. Мы будем использовать обозначения 1 и 0. В определенной интерпретации буквы принимают значения 1 или 0.

К высказываниям и буквам можно применять известные из курса дискретной математики логические связки или логические операции. При этом получаются формулы (формы). Формулы становятся высказываниями при подстановке всех значений букв.

Таблицы истинности основных логических операций.

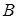
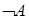
Более строго формула определяется так.

Определение. 1) Всякая буква есть формула.

2) Если , 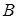- формулы, то формулами являются также , , , , .

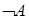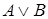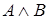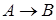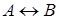3) Символ является формулой тогда и только тогда, когда это следует из 1) и 2).

В классической логике формулы принято заключать в круглые скобки, но в мы этого делать не будем. Для всякой формулы можно построить таблицу истинности.

Значение формулы 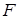в заданной интерпретации 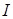обозначают 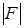(или , или ).

Часть формулы, которая сама является формулой, называется подформулой данной формулы.

Определение. Формула называется тавтологией, если она принимает только истинные значения при любых значениях букв.

Другими словами, тавтология – это тождественно истинная формула.

Установить, является ли формула тавтологией, можно:

– по таблице истинности,

– используя свойства логических операций.

Из курса дискретной математики известны основные логические эквивалентности (свойства логических операций), которые являются примерами тавтологий.

1. Коммутативность: , .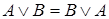

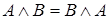2. Ассоциативность:

, .

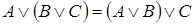3. Дистрибутивность:

, .

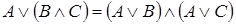4. Идемпотентность: , .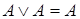

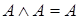5. Закон двойного отрицания: .

6. Закон исключения третьего: .

7. Закон противоречия: .

8. Законы де Моргана:

, .

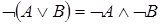9. Свойства операций с логическими константами:

, , , .

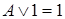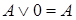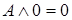Здесь , 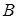и 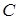– любые буквы.

Примеры. 1. Доказать, что формула является тавтологией.

Доказательство. Допустим, что при некоторых значениях букв (то есть в некоторой интерпретации)

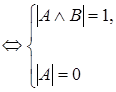
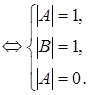
Приходим к противоречию, которое доказывает, что исходная формула – тавтология.

2. Доказать, что формула является тавтологией.

Доказательство. Эквиваленция истинна, если левая и правая части принимают одинаковые значения на некотором наборе значений букв.

Допустим, что при некоторых значениях букв

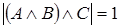
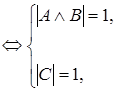
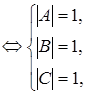
Следовательно, исходная формула – тавтология.

3. Доказать, что формула 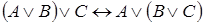является тавтологией.

Доказательство. Допустим, что при некоторых значениях букв

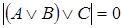
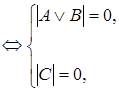
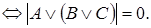
Следовательно, исходная формула – тавтология.

Таким образом, тождественную истинность импликации удобно доказывать от противного, а тождественную истинность эквиваленции установлением равенства значений левой и правой части.

Теорема. Пусть формулы и 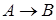– тавтологии. Тогда формула 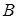– тавтология.

Доказательство. Пусть 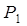, , 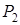…, 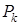– буквы в формулах и 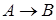. В теории булевых функций было доказано, что все булевы функции, а, следовательно, и формулы, можно считать зависящими от одного и того же количества букв. Рассмотрим некоторый набор значений , , 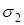…, , где , 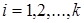. Подставим данный набор значений в формулы и 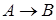вместо соответствующих букв. Формулы являются тавтологиями по условию теоремы, следовательно, 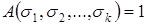и 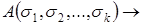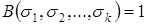. По таблице истинности импликации получаем, что 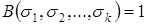. Поскольку набор значений , , 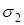…, был произволен, формула 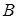– тавтология, что и требовалось доказать.

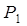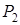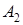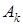Теорема. Пусть формула – тавтология, , , …, – буквы в формуле , , , …, – любые формулы. Тогда новая формула – тавтология.

Доказательство аналогично доказательству предыдущей теоремы.

В Содержание.

Date: 2015-09-24; view: 1317; Нарушение авторских прав