Глава 5. Предикаты

В исчислении высказываний нет предметных переменных, то есть переменных, которые могут принимать нелогические значения, например, числовые. Для того чтобы в логические исчисления могли быть включены нелогические константы и переменные, вводится понятие предиката.

Определение. n-местным предикатом на множестве называется -местная функция из множества 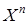во множество .

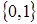Примеры. 1. Предикат на множестве – одноместный.

2. Предикат 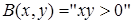на множестве 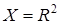– двуместный.

Если , то -местный предикат представляет собой -местную булеву функцию.

Нульместный предикат представляет собой высказывание.

Для каждого предиката областью истинности называется множество , на котором предикат принимает значение 1.

Примеры. 1. Для предиката на множестве область истинности .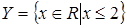

2. Для предиката 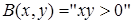на множестве 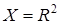область истинности .

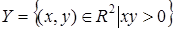Поскольку множество значений любого предиката лежит во множестве 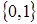, то с предикатами можно производить все операции алгебры логики, и все известные свойства логических операций обобщаются для предикатов. Рассмотрим эти свойства (для удобства в свойствах записываются одноместные предикаты):

3. Коммутативность:

, .

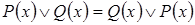2. Ассоциативность:

,

.

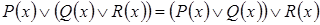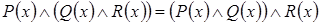3. Дистрибутивность:

,

.

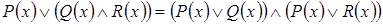4. Идемпотентность: , .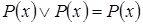

5. Закон двойного отрицания: .

6. Закон исключения третьего: .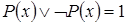

7. Закон противоречия: .

8. Законы де Моргана:

,

.

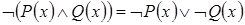9. Свойства операций с логическими константами:

, , , .

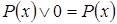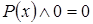Здесь , 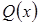и 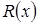– любые предикаты.

В то же время, для предикатов определены операции специального вида, которые называются кванторами.

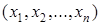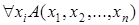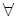Пусть дан -местный предикат на множестве , означающий, что для набора выполнено свойство , и пусть – одна из переменных. Тогда запись означает, что для всех значений переменной свойство выполнено. Символ называется квантором всеобщности (общности). Предикат 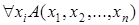является (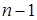)-местным. Он зависит от переменных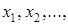 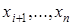. Если дан одноместный предикат 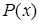, то утверждение представляет собой нульместный предикат, то есть истинное или ложное высказывание.

Пример. На множестве дан предикат . Высказывание ложно.

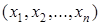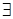Пусть дан -местный предикат на множестве , означающий, что для набора выполнено свойство , и пусть – одна из переменных. Тогда запись означает, что существует значение переменной , такое, что выполняется свойство . Символ называется квантором существования. Предикат является ()-местным. Если дан одноместный предикат 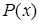, то утверждение представляет собой нульместный предикат, то есть истинное или ложное высказывание.

Пример. На множестве дан предикат . Высказывание истинно.

Отметим, что запись (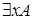) не подразумевает, что в формуле есть переменная .

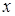Пусть дана запись (или 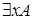). Переменная 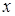называется переменной в кванторе, а – областью действия квантора.

Имеют место эквивалентности:

.	.
.	.

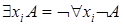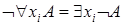Отметим, что список переменных в предикате мы будем указывать не всегда.

Предикат называется тождественно истинным (тождественно ложным), если при всех возможных значениях переменных он принимает значение 1(0).

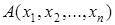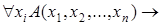
Теорема. Пусть – -местный предикат, – переменная в предикате. Тогда предикат является тождественно истинным.

Доказательство. Возьмем произвольный набор значений 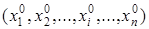переменных . Подставим этот набор в предикат 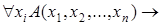. Получим высказывание:

.

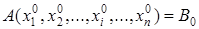Покажем, что это высказывание истинно. Возможны два случая.

1. 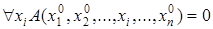, следовательно .

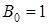2. .

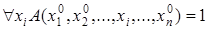Соотношение выполнено при любых значениях , следовательно, и при значении . При подстановке этого значения получаем:

.

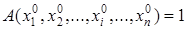Следовательно, по свойству импликации получаем, что 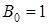, что и требовалось доказать.

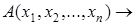
Теорема. Пусть – -местный предикат, – переменная в предикате. Тогда предикат является тождественно истинным.

Доказательство аналогично доказательству предыдущей теоремы.

Предикат называется выполнимым, если при некоторых значениях переменных он принимает значение 1.

Пример. Найти значение высказывания 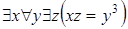. Предикат 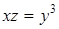определен на множестве .

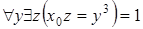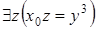Решение. Пусть . Эквивалентность имеет место тогда и только тогда, когда для некоторого . Это означает, что для некоторого предикат является тождественно истинным относительно , то есть для некоторого и для произвольного 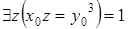. Последнее равносильно тому, что предикат 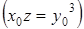выполним. Предикат действительно является выполнимым, поскольку он определен на множестве натуральных чисел. Таким образом, поскольку все переходы были равносильными, исходное высказывание истинно.

Предикаты могут быть выражены с помощью так называемых предикатных формул. Строгое определение формулы исчисления предикатов будет дано в следующей главе. Пока нужно учитывать, что формула становится предикатом, когда все переменные определены на некотором множестве, и определены все предикаты, входящие в формулу.

Справедливы эквивалентности:

, .

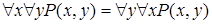Разноименные кванторы можно переставлять только следующим образом:

, .

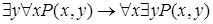Обратные формулы неверны.

Пример. Очевидно, что выска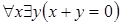зывание () истинно. Поменяем кванторы местами. Получим высказывание 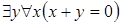, которое является ложным.

Выражения с кванторами можно преобразовывать следующим образом:

, .

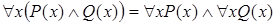Докажем первую эквивалентность. Пусть предикаты 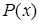и 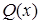одновременно тождественно истинны. Тогда тождественно истинным будет и предикат , следовательно, истинными будут высказывания 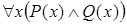, , , а также .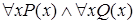

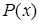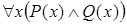Пусть теперь хотя бы один из предикатов (например, ) не является тождественно истинным. Тогда (по свойствам конъюнкции) тождественно истинным не будет и предикат , следовательно, ложным будет высказывание . Высказывания и 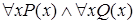также будут ложными.

Таким образом, обе части эквивалентности одновременно истинны или ложны, и эквивалентность доказана.

Замечание. Формула не эквивалентна формуле .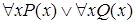

Доказательство. Рассмотрим обе формулы на множестве 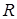. Пусть предикат , а предикат . Оба предиката не являются тождественно истинными. Предикат – тождественно истинный, и высказывание истинно. Высказывания и ложны, следовательно, ложно и высказывание 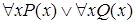. Таким образом, построен пример, когда формулы и 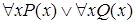принимают различные значения.

Тем не менее, справедливы эквивалентности:

.

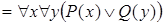Аналогично, формулы и не эквивалентны. Но справедливы эквивалентности:

.

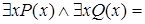
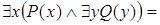
Имеют место формулы:

, ,

, .

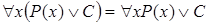Здесь 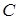не содержит переменной .

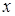Определение. Предикатная формула находится в приведенной форме, если в ней использованы только кванторные операции, а также операции инверсии, конъюнкции, дизъюнкции, причем инверсия относится только к предикатным буквам.

Определение. Предикатная формула находится в предваренной форме (предваренной нормальной форме), если она имеет вид , где 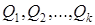- кванторы всеобщности или существования, а формула находится в приведенной форме и не содержит кванторов.

Пример. Записать формулу

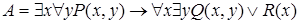
в предваренной нормальной форме.

Решение.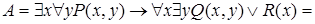

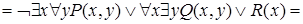
Полученная формула записана в приведенной форме. Для того чтобы квантор всеобщности можно было вынести за скобки, переобозначим переменные и выполним преобразования:

.

Рассмотрим предикат 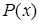, определенный на конечном множестве 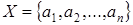. Если предикат 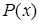является тождественно истинным, то истинными будут высказывания 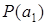, , …, 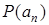. При этом истинными будут высказывания и конъюнкция … .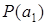

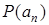Если же хотя бы для одного элемента 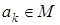будет ложно, то ложными будут высказывания и … .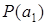

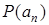Таким образом, имеет место эквивалентность … .

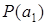
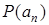Справедлива и аналогичная эквивалентность

… .

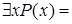
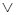
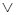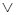
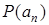Пример. Найти предикат, логически эквивалентный предикату , но не содержащий кванторов. Предикаты и 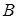определены на множестве .

Решение.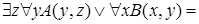

С помощью предикатов можно записывать различные математические утверждения.

Пример. Покажем, как можно записать утверждение: “числовая последовательность имеет пределом число ()”.

Решение. Запишем данное утверждение с помощью кванторов и обозначим его :

.

Запишем инверсию данного высказывания:

.

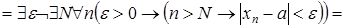
По известным формулам, инверсия импликации преобразуется следующим образом:

.

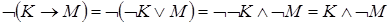Отсюда получаем:

.

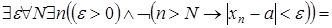
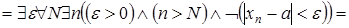
Утверждение 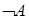означает, что , то есть число не является пределом числовой последовательности .

В Содержание.