Независимые однородные испытания

5.1 Биномиальное распределение. Схема испытаний Бернулли.

Биномиальным называют распределение вероятностей, определяемое формулой Бернулли. Закон назван биномиальным потому, что правую часть равенства можно рассматривать как общий член разложения бинома Ньютона.

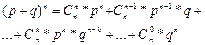
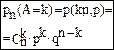(2.1) q=1-p

ξ			…	n
p			…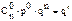

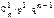
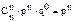
5.2 Локальная формула Муавра-Лапласа

Если n→∞, то в системе испытаний Бернулли вероятностную формулу приближенной формулой:

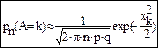
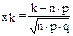
5.3 Распределение Пуассона. Закон редких явлений

Если 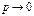или 1, 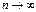, тогда применяется

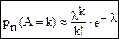
5.4 Наивероятнейшее число появлений заданного события А

n·p - q ≤ k ≤ n·p + p (2.4)

Если (n+1)·p - дробное число, то k= (n+1)·p

Если (n+1)·p - целое число, то k= (n+1)·p или k= (n+1)·p-1

5.5 Интегральная формула Муавра-Лапласа

Если в n- испытаниях событие А может появиться в каждом опыте с вероятностью р, то ка-кова вероятность того, что со-бытие А появится не менее k1 и не более k2 раз, т.е.: k1≤ A≤ k2.

Если n мало (n ≤10), то при ручном счете необходимо провести суммирование по формуле (2.1)

Если n большое (n→∞), тогда:

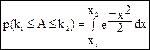(2.5) (первообразная не существует)

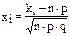
«Случайные величины и их характеристики»