Основы классического метода. Законы коммутации

Существуют два режима работы электрических цепей: установившийся (стационарный) и переходный (неустановившийся).

Под установившимся режимом понимается режим, при котором токи и напряжения в цепи могут существовать неограниченно долго, не изменяя своего характера, причем последний определяется видом ЭДС или видом заданных токов. Если в цепи действуют постоянные во времени ЭДС, то в установившемся режиме токи и напряжения на всех участках также постоянны во времени. Если ЭДС в цепи изменяются по синусоидальному закону, то токи и напряжения в установившемся режиме изменяются по тому же закону.

Под переходным режимом понимается процесс, возникающий в цепи при переходе от одного установившегося режима к другому. Этот переход вызывается коммутацией, под которой понимается: подключение цепи к источнику ЭДС, скачкообразное изменение ЭДС, отключение цепи от источника, короткое замыкание цепи, скачкообразное изменение параметров цепи и т. П

Реально процесс коммутации занимает конечный, хотя и весьма малый промежуток времени 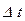. Если не интересоваться процессом в течение указанного промежутка времени 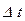, а рассматривать лишь процесс после того, как коммутация закончена, то можно считать, что коммутация совершается мгновенно (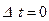). Так и поступают.

Допустим, что коммутация совершается мгновенно и происходит при 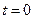. Обозначим момент времени, непосредственно прилегающий к моменту коммутации до коммутации – 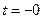; а момент времени, прилегающий к моменту коммутации, но после коммутации, через .

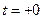Электрическая цепь, как правило, содержит такие элементы как конденсатор и индуктивная катушка. Эти элементы называют накопителями энергии. Энергия электрического поля конденсатора равна 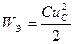; энергия магнитного поля индуктивной катушки равна .

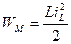Допустим, что при коммутации имеет мгновенное, но вполне определенное изменение мощности, сообщаемой цепи. Если потери на поглощение и на излучение малы, то вся эта мощность пойдет на увеличение энергии электромагнитного поля цепи. Это означает, что при всех мгновенных, но определенных по величине изменениях мощности, отдаваемой источником, фактическая энергия поля в системе не изменяется мгновенно, так что при коммутации энергия накопителей не может измениться, т.к. они обладают инерцией

.

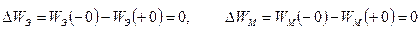Так как 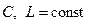, то следует

,

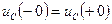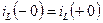
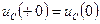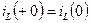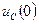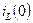Обычно обозначают , и называют и независимыми начальными условиями.

Таким образом, в момент коммутации напряжения на обкладках конденсаторов и токи в индуктивных катушках – непрерывные функции времени, другими словами: в момент коммутации остаются неизменными напряжения на обкладках конденсатора и токи в индуктивных катушках. Этот факт обычно называют законами коммутации.

Если до коммутации в момент времени 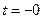имелись ток в катушке 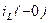и напряжение на конденсаторе 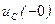, которые определяются процессом до коммутации, то говорят, что имеют место ненулевые начальные условия, причем под ними понимаются ток в катушке и напряжение на конденсаторе 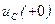непосредственно после коммутации, т.е. в момент времени .

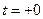Внимание. Очень важно различать значения токов и напряжений, имевших место до коммутации, от начальных значений тех же величин, в особенности, при использовании источников, характеризуемых разрывными функциями.

Согласно законам коммутации 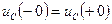; 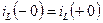. Если ток в катушке и напряжение на конденсаторе до коммутации были равны нулю, т.е. 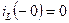, , 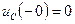то принято говорить, что имеют место нулевые начальные условия и по законам коммутации можно написать

, .

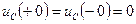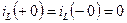Расчет переходных процессов в электрических цепях основан на решении интегро-дифференциальных уравнений цепи, составленных по законам Кирхгофа. Эти уравнения составляются для состояния цепи после коммутации. Они линейны, т.к. цепь – линейна.

В качестве переменных, относительно которых осуществляется решение, лучше выбрать ток, протекающий через индуктивность, либо напряжение на конденсаторе, т.к. они подчиняются законам коммутации.

Пусть заданы ЭДС. Тогда неизвестными будут токи во всех «p» ветвях. Число уравнений, подлежащих решению, будет равно «p». Допустим, что необходимо определить ток в k -ой ветви 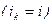. Тогда из указанных уравнений исключаем все другие токи и в результате получим дифференциальное уравнение с постоянными коэффициентами (т.к. цепь – линейная)

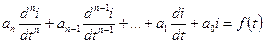. (1.1)

Порядок (n) уравнения определяется конфигурацией и характером цепи и числом ее накопительных элементов.

Порядок дифференциального уравнения можно определить следующим образом. Сначала определяются независимые контуры в схеме цепи. Определяется порядок каждого независимого контура. Он определяется только теми элементами, которые не использовались при составлении уравнений других контуров. Порядок всей схемы является суммой порядков всех отдельных контуров. Порядок независимого контура считается равным нулю, если контур состоит только из активных сопротивлений. Если контур содержит только индуктивную катушку или только конденсатор, то порядок контура равен единице; при этом наличие или отсутствие активных сопротивлений не имеет значения. Если в контуре есть индуктивная катушка и конденсатор, то его порядок равен двум.

Свободный член уравнения (1.1) – функция 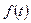определяет возмущение системы, которое может включать функцию, характеризующую источники (например, источники ЭДС), и несколько ее производных. В большинстве случаев функция 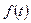- непрерывная функция времени, поэтому коэффициенты 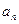уравнения (1.1) зависят только от параметров цепи.

Решение уравнения (1.1) можно записать 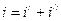, где 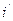есть частное решение неоднородного уравнения (1.1), 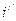есть общее решение однородного уравнения (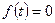). 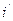- установившийся ток цепи в новом состоянии (после коммутации), 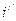- свободный (преходящий) ток, который существует только во время переходного процесса.

Для определения 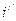необходимо найти корни характеристического уравнения .

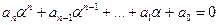Для линейных пассивных электрических цепей все коэффициенты характеристического уравнения – действительные и положительные.

При этом условии корни характеристического уравнения, если они являются простыми, могут быть:

· действительными и отрицательными;

· равными нулю;

· мнимыми, попарно сопряженными;

· комплексными с отрицательной действительной частью, попарно сопряженными.

Пусть корни этого уравнения простые (вещественные и разные по величине): 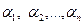. Следует еще раз отметить, что корни должны быть отрицательными числами. Тогда свободный ток ищется в виде

,

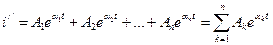а решение уравнения (1.1) записывается следующим образом

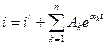, (1.2)

где 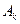есть постоянные, определяемые из начальных условий. Число этих постоянных равно «n», поэтому для их определения необходимы «n» уравнений. Эти уравнения получим следующим образом

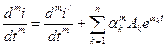. (1.3)

Внимание. Характер «свободной» составляющей не зависит от вида свободного члена 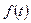(уравнение (1.1)), этот член влияет только на амплитуду «свободной» составляющей

Далее используем уравнение (1.2) и уравнения, получаемые из уравнения (1.3) при 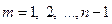. В левую часть этих уравнений подставим соответствующие значения 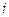, 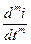при 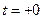, а для правой части положим .

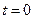Получим

,

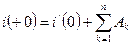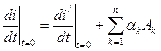, (1.4)

………………..

.

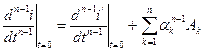Здесь величины, стоящие слева называются зависимыми начальными условиями. Они определяются с помощью независимых начальных услови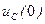й: и 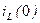. А они согласно законам коммутации равны токам в тех же катушках и напряжениям на тех же конденсаторах при 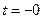. Поэтому для определения независимых начальных услови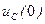й: и 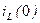, необходимо рассчитать установившийся режим до коммутации.

Для определения зависимых начальных условий 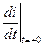,… 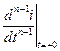нужно решить уравнения для момента после коммутации при .

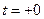Решая уравнения (1.4), находим постоянные А_k.

Следует отметить, что определение постоянных интегрирования при решении однородных дифференциальных уравнений представляет значительные трудности, которые можно полностью избежать, если пользоваться операторным методом (глава 2).

Если среди корней характеристического уравнения есть кратные и комплексные числа, то общее решение однородного уравнения имеет другой вид.

Пусть 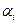есть кратный корень m -й кратности. Тогда свободный ток равен

.

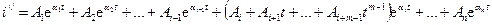Если среди корней характеристического уравнения есть комплексные числа, то они могут быть только попарно сопряженными с отрицательными вещественными частями (если коэффициенты характеристического уравнения - действительные числа). Пусть 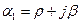, , 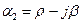а все другие корни вещественные числа. Тогда свободный ток равен

.

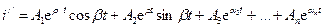Внимание. Корни характеристического уравнения можно найти, не выводя и не решая последнего. Для этого находится выражение для входного операторного сопротивления исследуемой схемы относительно двух зажимов, получающихся в результате размыкания любой ветви схемы (если в схеме нет короткозамкнутых ветвей). Полученное выражение приравнивается нулю, в результате решения этого уравнения находятся корни, которые являются корнями характеристического уравнения.

Date: 2015-09-17; view: 732; Нарушение авторских прав