Доказательство. Заметим, прежде всего, что если правые части bi (i = 1,2, ,m) системы линейных уравнений равны нулю

Заметим, прежде всего, что если правые части b_i (i = 1,2,…,m) системы линейных уравнений 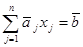равны нулю, то, так как ранг матрицы А равен m, вектор 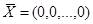является вырожденным опорным планом задачу линейного программирования. Поэтому в дальнейшем будем предполагать, что среди b_i есть отличные от нуля.

Пусть вектор 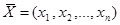- план, но не опорный план задачи линейного программирования с к строго положительными компонентами. Не нарушая общности, будем считать, что строго положительными являются первые к компонент вектора 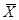, тогда имеет место равенство 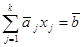(3.30)

Так как вектор 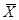- не опорный план, то согласно определению опорного плана задачи линейного программирования векторы 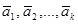линейно зависимы, то есть существуют действительные числа 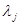не все равные нулю и такие, что 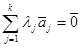(3.31)

Введём обозначение

(3.32)

Изменение знака в (3.31) можно всегда добиться, чтобы μ было положительным.

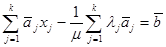Умножим левую и правую части (3.31) на 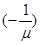и полученное равенство сложим с (3.30), будем иметь

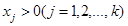или, так как

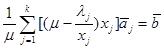
(3.32)

В силу (3.32) 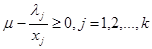(3.33)

и обязательно существует такое j, для которого в соотношении (3.33) имеет место равенство.

Положим для определённости, что .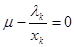

Таким образом, мы построили план задачи линейного программирования, j-я компонента которого есть 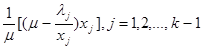, а остальные n-k+1 компонент равны нулю.

Если при этом векторы 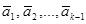оказались линейно зависимыми, то рассуждая аналогично, получим план задачи линейного программирования, у которого k-2 строго положительных компонент и так далее до тех пор, пока не построим такой план задачи линейного программирования с l (l≤ k) строго положительными компонентами, что соответствующие этим компонентам векторы 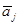будут линейно независимыми. Так по предложению среди b_i есть отличные от нуля, то l ≠0.

Согласно определению опорного плана ЗЛП построенный план является при l = m невырожденным, а при l < m вырожденным опорным планом задачи линейного программирования.

Теорема доказана.

5. Основные теоремы линейного программирования: сформулировать все, доказать теорему об оптимальности выпуклой комбинации планов ЗЛП (теорема 4).

Теорема 1. (о крайней точке) Опорный план ЗЛП является крайней точкой множества P’ и наоборот.

Следствие 1. Крайняя точка множества P’ может иметь не более m строго положительных компонент.

Следствие 2. Число крайних точек множества P’ конечно не превышает .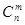

Следствие 3. Если множество P’ ограниченное, то оно является выпуклым многогранником.

Теорема 2 (о существовании опорного плана или решения ЗЛП) Если линейная форма 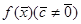ограничена сверху на непустом множестве P’, то ЗЛП разрешима, то есть существует такая точка 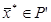, что .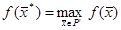

Теорема 3 Если множество P’ не пусто, то оно имеет опорный план (или крайнюю точку).

Теорема 4. Пусть векторы - планы задачи линейного программирования. Тогда вектор

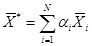
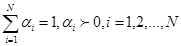
(3.34)

где (3.35)

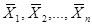будет решением задачи линейного программирования тогда и только тогда, когда её решением является каждый из векторов.

Теорема 5 Пусть вектор 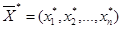является решением задачи линейного программирования. Тогда существует опорный план, на котором функция 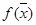достигает своего глобального максимума.

(теорема 4 об оптимальности выпуклой комбинации планов ЗЛП) Пусть векторы 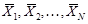планы задачи линейного программирования. Тогда вектор 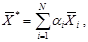где 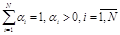будет решением задачи ЗЛП тогда и только тогда, когда её решением является каждый из векторов .

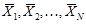Доказательство:

Пусть каждый из векторов 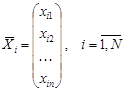является решением ЗЛП, т.е. Тогда 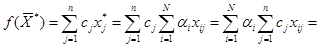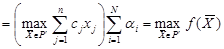т.е. вектор 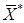, также является решением ЗЛП. Обратно, пусть вектор 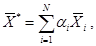где 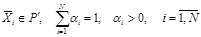является решением ЗЛП. Предположим, что среди векторов 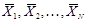есть хотя бы один вектор 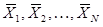, который не является решением ЗЛП, т.е. имеет место следующее неравенство: 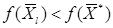Тогда будем иметь

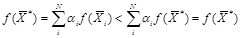Получили противоречие, следовательно, каждый из векторов 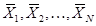есть решение ЗЛП. Теорема доказана.

6. Основные теоремы линейного программирования: сформулировать все, доказать теорему о существовании оптимального опорного плана ЗЛП (теорема 5).

Теорема 1. (о крайней точке) Опорный план ЗЛП является крайней точкой множества P’ и наоборот.

Следствие 1. Крайняя точка множества P’ может иметь не более m строго положительных компонент.

Следствие 2. Число крайних точек множества P’ конечно не превышает .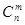

Следствие 3. Если множество P’ ограниченное, то оно является выпуклым многогранником.

Теорема 2 (о существовании опорного плана или решения ЗЛП) Если линейная форма 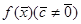ограничена сверху на непустом множестве P’, то ЗЛП разрешима, то есть существует такая точка 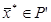, что .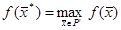

Теорема 3 Если множество P’ не пусто, то оно имеет опорный план (или крайнюю точку).

Теорема 4. Пусть векторы - планы задачи линейного программирования. Тогда вектор

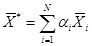
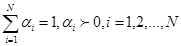
(3.34)

где (3.35)

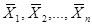будет решением задачи линейного программирования тогда и только тогда, когда её решением является каждый из векторов.

Теорема 5 Пусть вектор 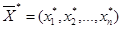является решением задачи линейного программирования. Тогда существует опорный план, на котором функция 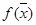достигает своего глобального максимума.

Date: 2015-09-18; view: 652; Нарушение авторских прав