
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Каноническая ЗЛП
Основная ЗЛП
ЗЛП во многих случаях оказывается ассоциированной с задачей распределительного типа или с задачей производственного планирования, в которой требуется распределить ограниченные ресурсы по нескольким видам производственной деятельности.
Такую ЗЛП можно поставить следующим образом: найти значения переменных Х1,Х2,…,Хn, максимизирующие линейную форму
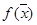 =
= 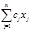 (3.4)
(3.4)
при условиях
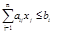 , i= 1,…,m (3.5)
, i= 1,…,m (3.5)
xj ³0, j=1,…,n (3.6)
или в векторно-матричной форме
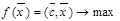 (3.7)
(3.7)
A 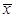 £
£ 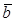 (3.8)
(3.8)
 x ³
x ³ 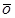 , (3.9)
, (3.9)
где 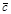 =(с1,с2,…,сn);
=(с1,с2,…,сn); 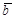 =(b1,b2,…,bm); А=(aij) – матрицы коэффициентов ограничений (3.5). Задача (3.4)- (3.6) или (3.7) – (3.9) называется основной ЗЛП. Основная ЗЛП является частным случаем общей ЗЛП при m1=m, p=n.
=(b1,b2,…,bm); А=(aij) – матрицы коэффициентов ограничений (3.5). Задача (3.4)- (3.6) или (3.7) – (3.9) называется основной ЗЛП. Основная ЗЛП является частным случаем общей ЗЛП при m1=m, p=n.
Каноническая ЗЛП
Для построения общего метода решения ЗЛП разные формы ЗЛП должны быть приведены к некоторой стандартной форме, называемой канонической задачей линейного программирования (КЗЛП).
В канонической форме
1. все функциональные ограничения записываются в виде равенств с неотрицательной правой частью;
2. все переменные неотрицательны;
3. целевая функция подлежит максимизации
Таким образом, КЗЛП имеет вид
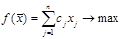 (3.10)
(3.10)
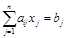 ,
, 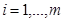 (3.11)
(3.11)
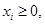
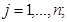
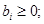
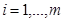 (3.12)
(3.12)
или в векторно-матричной форме
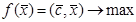 (3.13)
(3.13)
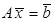 (3.14)
(3.14)
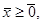
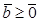 (3.15)
(3.15)
КЗЛП является частным случаем общей ЗЛП при m1=0, p=n
Любую ЗЛП можно привести к каноническому виду, используя следующие правила:
а) максимизация целевой функции 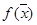 = c1x1+…+cnxn равносильна минимизации целевой функции -
= c1x1+…+cnxn равносильна минимизации целевой функции - 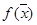 =-c1x1 -…-cnxn;
=-c1x1 -…-cnxn;
б) ограничение в виде неравенства, например, 3Х1+2Х2-Х3£6, может быть приведено к стандартной форме 3Х1+2Х2-Х3+Х4=6, где новая переменная Х4 неотрицательна. Ограничение Х1 -Х2+3Х3³10 может быть приведено к стандартной форме Х1 -Х2+3Х3-Х5=10, где новая переменная Х5 неотрицательна;
в) если некоторая переменная Хk может принимать любые значения, а требуется, чтобы она была неотрицательная, ее можно привести к виду 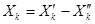 , где
, где 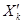 ³0 и
³0 и 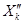 ³0.
³0.
Max f (x) = 3X1 + 2X2
X1 + 2X2 ≤ 11
2X1 - X2 ≥ 5
X1 + 3X2 = 14
X2 ≥ 0
КЗЛП:
F(x)=3х1+2х2+0х3+0х4
Х1+2х2+х3=11
2х1-х2-х4=5
Х1+3х2+0х3+0х4=14
Х1,2,3,4 ≥ 0
2. Алгоритм графического метода решения ЗЛП.
Решить ЗЛП графическим методом:
Minf (x) = 4х1+ 3х2
х1+ 2х2 £ 12
х1+ 2х2³3
2х1 + х2£ 12
х1³ 0, х2 ³ 0
Графическим методом целесообразно решать ЗЛП, содержащие не более двух переменных.
Алгоритм графического метода рассмотрим применительно к задаче:
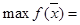 3Х1 + 2Х2 (3.16)
3Х1 + 2Х2 (3.16)
при

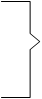 Х1 + 2Х2
Х1 + 2Х2 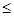 6 (а)
6 (а)
2Х1 + Х2 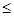 8 (б)
8 (б)
Р = Х1+0,8Х2 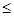 5 (в) (3.17)
5 (в) (3.17)
-Х1 + Х2 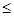 1 (г)
1 (г)
Х2 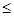 2 (д)
2 (д)
Х1 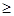 0, Х2
0, Х2 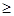 0 (е)
0 (е)
Шаг 1. Строим область допустимых решений (3.17) - область Р, т.е. геометрическое место точек, в котором одновременно удовлетворяются все ограничения ЗЛП. Каждое из неравенств (а)-(д) системы ограничений (3.17) задачи геометрически определяет полуплоскость соответственно с граничными прямыми:
Х1 + 2Х2 = 6 (а)
2Х1 + Х2= 8 (б)
Х1+0,8Х2= 5 (в)
-Х1 + Х2= 1 (г)
Х2= 2 (д)
Условия неотрицательности переменных (е) ограничивают область допустимых решений первым квадратом. Области, в которых выполняются соответствующие ограничения (3.17) в виде неравенств, указываются стрелками, направленными в сторону допустимых значений переменных (рис. 3.1).
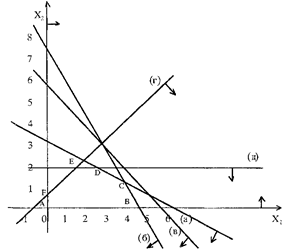
Рис. 3.1
Если система неравенств (3.17) совместна, область ее решений есть множество точек, принадлежащих всем указанным полуплоскостям.
Полученная таким образом область допустимых решений Р - планов ЗЛП (рис. 3.1) есть многоугольник ABCDEF - замкнутое, ограниченное, выпуклое множество с шестью крайними или угловыми точками: A, B, C, D, E, F.
Шаг 2. Строим вектор-градиент 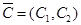 линейной формы
линейной формы 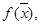
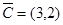 , указывающий направления возрастания функции
, указывающий направления возрастания функции 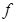 .
.
Шаг 3. Строим прямую С1Х1 +С2Х2 = const - линию уровня функции 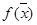 , перпендикулярную вектору-градиенту
, перпендикулярную вектору-градиенту 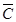 :
:
3Х1 + 2Х2 = const (рис.3.2)
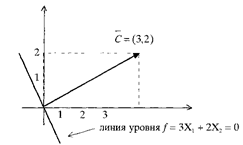
Рис. 3.2
Шаг 4. В случае максимизации 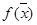 передвигают прямую 3Х1 + 2Х2 = const в направлении вектора
передвигают прямую 3Х1 + 2Х2 = const в направлении вектора 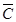 до тех пор, пока она не покинет область Р. Крайняя точка (или точки) области, в которой линия уровня покидает допустимую область, и является решением задачи (рис. 3.3).
до тех пор, пока она не покинет область Р. Крайняя точка (или точки) области, в которой линия уровня покидает допустимую область, и является решением задачи (рис. 3.3).
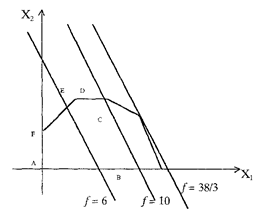
Крайняя точка С - точка максимума 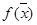 , С =
, С = 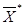 лежит на пересечении прямых (а) и (б). Для определения ее координат решим систему уравнений:
лежит на пересечении прямых (а) и (б). Для определения ее координат решим систему уравнений:
Х1 + 2Х2 = 6
2Х1 + Х2 = 8.
Откуда Х*1 = 10/3; X*2 = 4/3 или 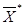 = (10/3; 4/3).
= (10/3; 4/3).
Подставляя значения Х*1 и X*2 в функцию 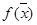 , найдем
, найдем
max 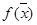 =
=  = 3 . 10/3 + 2 . 4/3 = 38/3.
= 3 . 10/3 + 2 . 4/3 = 38/3.
Замечания.
1. В случае минимизации 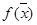 прямую С1Х1 +С2Х2 = const надо перемещать в направлении (-
прямую С1Х1 +С2Х2 = const надо перемещать в направлении (- 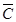 ), противоположном
), противоположном 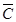 .
.
2. Если допустимая область решений Р представляет собой неограниченную область и прямая при движении в направлении вектора 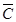 (или противоположном ему) не покидает Р, то в этом случае
(или противоположном ему) не покидает Р, то в этом случае 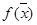 не ограничена сверху (или снизу), те
не ограничена сверху (или снизу), те 
(или 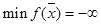 ).
).
3. Основные теоремы линейного программирования: сформулировать все, доказать теорему о крайней точке (Т 1).
Теорема 1. (о крайней точке) Опорный план ЗЛП является крайней точкой множества P’ и наоборот.
Следствие 1. Крайняя точка множества P’ может иметь не более m строго положительных компонент.
Следствие 2. Число крайних точек множества P’ конечно не превышает 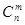 .
.
Следствие 3. Если множество P’ ограниченное, то оно является выпуклым многогранником.
Теорема 2 (о существовании опорного плана или решения ЗЛП) Если линейная форма 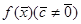 ограничена сверху на непустом множестве P’, то ЗЛП разрешима, то есть существует такая точка
ограничена сверху на непустом множестве P’, то ЗЛП разрешима, то есть существует такая точка 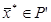 , что
, что 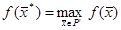 .
.
Теорема 3 Если множество P’ не пусто, то оно имеет опорный план (или крайнюю точку).
Теорема 4. Пусть векторы - планы задачи линейного программирования. Тогда вектор
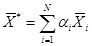
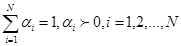
(3.34)
где (3.35)
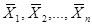 будет решением задачи линейного программирования тогда и только тогда, когда её решением является каждый из векторов.
будет решением задачи линейного программирования тогда и только тогда, когда её решением является каждый из векторов.
Теорема 5 Пусть вектор 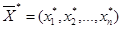 является решением задачи линейного программирования. Тогда существует опорный план, на котором функция
является решением задачи линейного программирования. Тогда существует опорный план, на котором функция 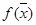 достигает своего глобального максимума.
достигает своего глобального максимума.
Теорема 1 (о крайней точке) Опорный план (вектора a линейно независимы) КЗЛП является крайней точкой множества P` и наоборот. Доказательство. Пусть вектор 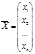 - опорный план ЗЛП, у которого компоненты
- опорный план ЗЛП, у которого компоненты 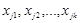 строго положительные, а остальные (n-k) компонент равны нулю. Тогда согласно определению опорного плана векторы
строго положительные, а остальные (n-k) компонент равны нулю. Тогда согласно определению опорного плана векторы 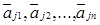 линейно независимы. Предположим, что вектор
линейно независимы. Предположим, что вектор 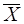 не является крайней точкой множества, т.е. существуют векторы
не является крайней точкой множества, т.е. существуют векторы
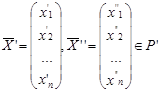
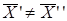 и
и 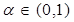 такие что
такие что 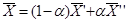 . Векторы
. Векторы 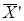 и
и 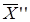 - планы ЗЛП. Это означает, во-первых, что компоненты векторов
- планы ЗЛП. Это означает, во-первых, что компоненты векторов 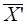 и
и 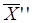 неотрицательные и ровно k компонент данных векторов могут быть строго положительными. Остальные (n-k) компонент каждого из этих векторов равны нулю. Во-вторых, компоненты векторов
неотрицательные и ровно k компонент данных векторов могут быть строго положительными. Остальные (n-k) компонент каждого из этих векторов равны нулю. Во-вторых, компоненты векторов 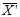 и
и 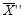 удовлетворяют функциональным ограничениям
удовлетворяют функциональным ограничениям 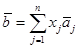 ЗЛП. Следовательно
ЗЛП. Следовательно 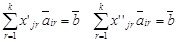 Вычитая из первого равенства второе получим
Вычитая из первого равенства второе получим 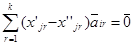 так как векторы
так как векторы  линейно независимы, то следует что
линейно независимы, то следует что 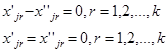 Следовательно
Следовательно 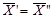 Получено противоречие, следовательно
Получено противоречие, следовательно 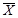 -крайняя точка множества
-крайняя точка множества 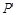 .
.
4. Основные теоремы линейного программирования: сформулировать все, доказать теорему о существовании опорного плана (теорема 3).
Теорема 1. (о крайней точке) Опорный план ЗЛП является крайней точкой множества P’ и наоборот.
Следствие 1. Крайняя точка множества P’ может иметь не более m строго положительных компонент.
Следствие 2. Число крайних точек множества P’ конечно не превышает 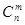 .
.
Следствие 3. Если множество P’ ограниченное, то оно является выпуклым многогранником.
Теорема 2 (о существовании опорного плана или решения ЗЛП) Если линейная форма 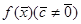 ограничена сверху на непустом множестве P’, то ЗЛП разрешима, то есть существует такая точка
ограничена сверху на непустом множестве P’, то ЗЛП разрешима, то есть существует такая точка 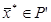 , что
, что 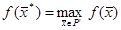 .
.
Теорема 3 Если множество P’ не пусто, то оно имеет опорный план (или крайнюю точку).
Теорема 4. Пусть векторы - планы задачи линейного программирования. Тогда вектор
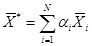
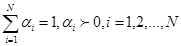
(3.34)
где (3.35)
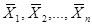 будет решением задачи линейного программирования тогда и только тогда, когда её решением является каждый из векторов.
будет решением задачи линейного программирования тогда и только тогда, когда её решением является каждый из векторов.
Теорема 5 Пусть вектор 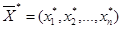 является решением задачи линейного программирования. Тогда существует опорный план, на котором функция
является решением задачи линейного программирования. Тогда существует опорный план, на котором функция 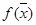 достигает своего глобального максимума.
достигает своего глобального максимума.
Теорема 3
Если множество P’ не пусто, то оно имеет опорный план (или крайнюю точку).
Date: 2015-09-18; view: 851; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |