
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Теорема о линейной независимости ортогональной системы векторов евклидова пространства
12. Ортогональный и ортонормированный базис евклидова пространства. Процесс ортогонализации.
Пусть 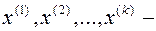 некоторые системы элементов евклидового пространства. Данная система векторов наз. ортогональной, если
некоторые системы элементов евклидового пространства. Данная система векторов наз. ортогональной, если 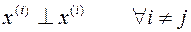 .
.
Теорема: всякая система попарно ортогональна ненулевых векторов линейно независима.
Док-во: пусть 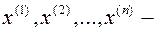 ортогональная система векторов, покажем, что она линейно независима:
ортогональная система векторов, покажем, что она линейно независима:
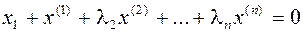 , где
, где 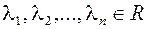 . Умножим это равенство скалярно на вектор
. Умножим это равенство скалярно на вектор 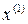 :(Лена, я тебя очень люблю(твой Сергей))
:(Лена, я тебя очень люблю(твой Сергей))
 ,
,
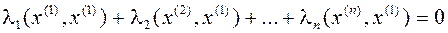
 , тогда
, тогда 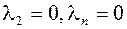 .
.
Замечание: если ортогональная система ненулевых векторов содержит n-векторов, где n-размерность пространства, то данная система векторов является базисом пространства. Если кроме того в ортогональном базисе все векторы имеют единую систему, то базис называется ортонормированным. (Лена, я тебя очень люблю(твой Сергей))
Теорема: во всяком n-мерном евклидовом пространстве существует ортонормированный базис.
Док-во: пусть 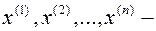 какой-нибудь базис. По данному базису будем строить ортонормированный базис
какой-нибудь базис. По данному базису будем строить ортонормированный базис 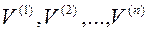 .
.
 - выберем (в качестве
- выберем (в качестве 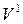 выберем
выберем 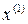 ).
).
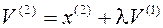 , число
, число  подберем таким образом, чтобы вектор
подберем таким образом, чтобы вектор  был ортогонален
был ортогонален  ,
,  .
.
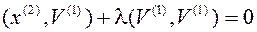
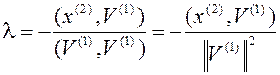 .
.
 , где
, где 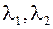 - такие, что
- такие, что  - ортогонален двум предыдущим.
- ортогонален двум предыдущим.
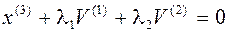 .
.
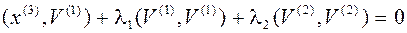 .
.
 .
.
Аналогично получим 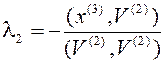 ,
, 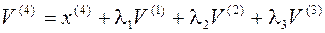 .
.
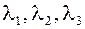 - такие, что
- такие, что 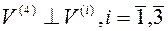 .
.
Продолжим этот процесс дальше, мы получим ортогональный базис. Такой процесс получения ортогонального базиса наз. процессом ортогонализации. Покажем как из ортогонального базиса получить ортонормированный.
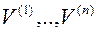 ,
, 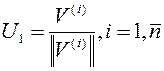 .
.
В результате 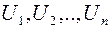 остается ортогональным базисом и все векторы в этом базисе имеют норму (1)
остается ортогональным базисом и все векторы в этом базисе имеют норму (1)
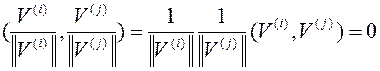 .
.
Date: 2015-09-03; view: 8073; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |