Основные соотношения и понятия

Прежде чем повторить о механическом движении, нужно выбрать систему отсчета (СО). В механике Ньютона СО представляет собой совокупность трех элементов: тела отсчета, относительно которого рассматривается движение, линеек для измерения длин, расстояний, и часов для измерения времени. Подразумевается, что часы запускаются в момент начала самого первого из интересующих нас движений, так что если буквой t обозначить показание часов, то всегда t³0. После выбора СО для написания движения необходимо выбрать систему координат (СК). Ограничимся далее рассмотрением движений, происходящих в одной плоскости. Тогда в этой плоскости чаще всего выбирают декартову прямоугольную систему координат (рис. 1). Радиус-вектор точки Р связан с ее координатами (х, у) соотношением

, (1.1)

где , – орты координатных осей, , .

Модуль радиуса вектора

, (1.2)

а угол a между осью х и вектором обычно определяют из соотношения .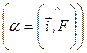

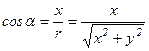, (1.3)

при этом cosa называют направляющим косинусом. При решении конкретных задач выбор декартовой системы координат сводится к указанию, в какой точке, связанной с условием задачи, выбирается начало координат, и куда направляются оси. Достаточно часто используется также полярная система координат, задание которой сводится к указанию оси, от которой отсчитываются углы (ось Ох), и указания положительного направления отсчета углов (против часовой стрелки). Полярными координатами точки Р является пара (r, a), что соответствует образно говоря, туристическому способу указания положения: указывается дальность и азимут. Связи между декартовыми и полярными координатами вытекают из вышеприведенных формул:

. (1.4)

Аналогичные соотношения справедливы для любого вектора на плоскости, который может быть задан либо указанием модуля вектора 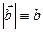и угла a между осью Ох и вектором : , т.е. парой (b, a), либо заданием пары проекций (координат) вектора (b_к, b_у):

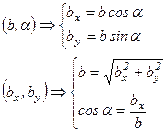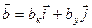, . (1.5)

Моделью тела, размеры и форма которого, а также движение внутри его в рассматриваемых условиях несущественны, является материальная точка (частица). При движении материальной точки ее декартовы или полярные координаты изменяются, т.е. являются функциями времени:

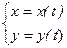или 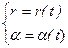. (1.6)

Если эти функции известны, то говорят, что задан кинематический закон движения. Кинематический закон движения в декартовой прямоугольной системе координат компактно можно записать в виде:

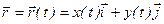. (1.7)

В полезных координатах кинематический закон движения соответствует так называемому радарному способу описания движения, когда указывается закон изменения расстояния от начальной точки и закон изменения азимута (угла между осью и направлением на движущуюся точку).

Кривая, описываемая частицей при движении, называется траекторией. Ее уравнение в декартовых координатах получается путем исключения времени t из кинематического закона движения (1.6):

(1.8)

Аналогично можно получить уравнение траектории в полезных координатах. В отличие от математических кривых, на траектории есть начальная точка, соответствующая положению частицы при t=0, а также стрелкой указывается направления движения (траектория является так называемой ориентированной кривой). Иногда один и тот же участок траектории может проходиться частицей несколько раз в противоположных направлениях. Это имеет место, например, при колебаниях.

Путем называется длина дуги траектории, отсчитываемая вдоль направления движения. Путь – скалярная величина. По определению функция s=s(t) является неубывающей функцией времени, при чем при t=0, s=0. Поскольку элемент длины дуги может быть записан в виде

,

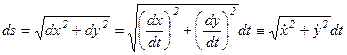то функция s(t) находится из соотношения .

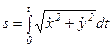. (1.9)

Если задано уравнение траектории, указано положение частицы на траектории при t=0, направление движения частицы по траектории и зависимость s=s(t), то говорят, что задан естественный закон движения частицы. Формулы (1.8) и (1.9) описывают переход от кинематического закона движения в декартовых координатах к естественному закону движения. Возможен и обратный переход, но мы его в общем случае рассматривать не будем (для движения по окружности этот переход будет рассмотрен на примере).

Вектором перемещения частицы за промежуток времени Dt от момента t₁ до момента t₂ Dt=t₂–t₁ называется вектор

.

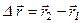Его проекции на координатные оси равны:

.

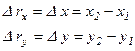Тогда

.

Модуль вектора перемещения

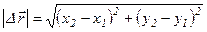, (1.10)

а направляющий косинус этого вектора

. (1.11)

Если обозначить , то, очевидно

,

причем знак равенства имеет место для прямолинейного движения без точек поворота.

Средней путевой скоростью называется скалярная величина

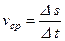. (1.12)

В СИ путь измеряется в метрах (м), а время – в секундах (с), поэтому единица v_ср есть

.

Положив Dt=1 с, имеем 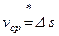(знак называется численным равенством): средняя путевая скорость численно равна пути, проходимому частицей за 1 с.

Средняя скорость перемещения – это вектор, определяемый соотношением

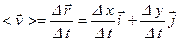. (1.13)

Ее направление совпадает с направлением вектора перемещения, а модуль равен

. (1.14)

Мгновенная скорость точки – это векторная величина, определяемая соотношением

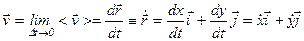. (1.15)

Проекции скорости на координатные оси:

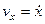, . (1.16)

Модуль вектора мгновенной скорости и его направление определяются соотношением

. (1.17)

.

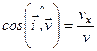Согласно (1.9), имеем

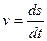. (1.18)

Формулы (1.15)–(1.17) определяют вектор скорости, когда задан кинематический закон движения в декартовых координатах, а формула (1.18) определяет модуль скорости, когда задан естественный закон движения s=s(t). Направлен вектор 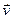по касательной к траектории (на рис. 1.2 показано направление вектора скорости 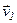в момент времени t₁) и может быть записан в виде:

, (1.19)

где – единичный вектор касательной. В полезных координатах вектор скорости может быть представлен в виде (рис. 1.3)

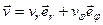, (1.20)

где 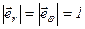– единичные взаимоперпендикулярные векторы;

. (1.21)

Первое слагаемое в формуле (1.20) характеризует быстроту изменения расстояния от частицы до начала координат, а второе – быстроту движения в направлении перпендикулярном радиальному.

Оптимальной скоростью частицы 2 относительно частицы 1 называется величина

. (1.22)

Эта скорость представляет собой скорость второй частицы относительно системы отсчета, связанной с первой частицей и движущейся поступательно. Расстояние l между частицами 1 и 2 определяется формулой

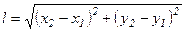. (1.23)

Не следует путать с модулем вектора перемещения, который определяется формулой (1.10): в формуле (1.10), например, х₂ и х₁ – это координаты одной и той же частицы в разные моменты времени t₁ и t₂, т.е. х₁=х(t₁), х₂=х(t₂), а в формуле (1.23) х₂ и х₁ – это координаты частиц 1 и 2 в один и тот же момент времени. Вообще говоря, расстояние между частицами с течением времени изменяется, и можно говорить о скорости изменения этого расстояния, т.е. о скорости сближения-удаления частиц:

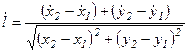. (1.24)

Поскольку, вообще говоря, скорость частицы с течением времени изменяется, можно ввести величину показывающую, как быстро изменяется скорость, подобно тому, как скорость показывает, как быстро изменяется положение частицы. Эта величина называется ускорением частицы. Сначала вводится понятие среднего ускорения:

, (1.25)

где ,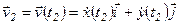

.

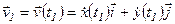Модуль среднего ускорения

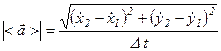, (1.26)

а его направление определяется из соотношения

. (1.27)

На рис. 1.4 показаны схематично векторы , , 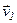, 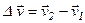и 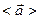. Поскольку вектор средней скорости характеризует движение частицы за промежуток времени Dt=t₂–t₁, то он не связан с частицей в какой-то определенный момент времени в указанном интервале, и поэтому его изображение на рисунке с привязкой к конкретному моменту времени носит условный характер (на рис. 1.4 вектор изображен в момент t₁). То же справедливо и в отношении вектора среднего ускорения (на рис. 1.4 он показан в момент t₂). Мгновенное ускорение получается в результате предельного перехода при Dt®0 и при задании кинематического закона движения определяется соотношениями:

. (1.28)

При естественном способе задания движения ускорение записывается в виде:

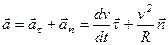, (1.29)

где 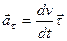– тангенциальное ускорение, 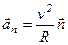– нормальное ускорение, – единичный вектор касательной к траектории и нормали, направленной в сторону вогнутости траектории соответственно (рис. 1.5а и 1.5б).

Величина R, входящая в выражение для нормального ускорения, называется радиусом кривизны траектории. Не вдаваясь в тонкости математического обоснования, скажем, что маленький участок любой кривой в первом приближении можно заменить участком прямой линии, а во втором – участком (дугой) подходящей окружности, которая называется соприкасающейся окружностью. Радиус этой соприкасающейся окружности называется радиусом кривизны R кривой, а ее центр С – центром кривизны. Разумеется, и радиус R и координаты центра кривизны для данной точки кривой не зависят от закона движения s=s(t) частицы по этой кривой и определяются формулами:

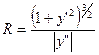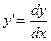, где , (1.30)

,

Эти же величины, конечно, могут быть найдены и непосредственно из кинематического закона движения:

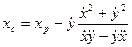, , (1.31)

Из формул (1.29) вытекает смысл каждой из составляющих полного ускорения . Тангенциальное (касательное) ускорение направлено по касательной к траектории и в случае постоянства модуля скорости равно нулю. Если скорость по модулю возрастает (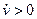 – ускорение движения), то 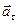сонаправлено со скоростью, если скорость убывает ( 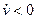– замедленное движение), то (рис. 1.5а и 1.5б соответственно). Поскольку

и , (1.32)

то проекции касательного ускорения на оси координат равны

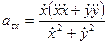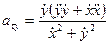, . (1.33)

Итак, касательное ускорение характеризует быстроту изменения модуля скорости. Нормальное ускорение при движении по прямой (R=∞) равно нулю и, следовательно, характеризует быстроту изменения направления вектора скорости. Поскольку 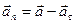, то

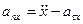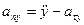, . (1.34)

Используя выражения (1.33) и (1.34), можно стандартным образом найти угол между осью х и векторам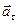и и . При движении по окружности, лежащей в плоскости хоу, при заданном радиусе r окружности положение частицы определяется углом j между радиус-вектором частицы и осью х, отсчитываемом, как обычно, против часовой стрелки: j=j(t) (рис. 1.6). Угловая скорость w и угловое ускорение e определяются соотношениями:

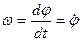, . (1.35)

При этом единицы их измерения: , .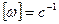

Знаки величин w и e иллюстрирует рис. 1.7, на котором представлен график j(t) и области положительных и отрицательных значений w и e.

Поскольку в этом случае для радиус-вектора имеем

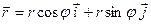, (1.36)

то

, (1.37)

где .

Поскольку 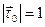и , то 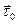– единичный вектор касательной, связанный, однако, не с направлением движения по окружности, а с положительным направлением отсчета угла j. Поэтому , где – единичный вектор касательной направленный по скорости частицы (см. формулу 1.19), где знак плюс соответствует w>0, а минус – w<0. Поэтому 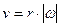. Дифференцируя (1.37), получим

,

где 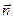– единичный вектор нормали к окружности, направленной к центру

Первое слагаемое представляет собой касательное ускорение, а второе – нормальное или центростремительное:

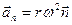, . (1.38)

Заметим, наконец, что при заданном законе j=j(t) изменение угла кинематический закон движения и естественный закон движение получаются элементарно:

, . (1.39)

Кинематика изучает лишь способы описания движения частиц, не интересуясь причинами, по которым это движение выглядит так или иначе. В принципе, для описания движения в кинематике можно выбрать любую систему отсчета и любую систему координат в ней, поэтому говорят о кинематической эквивалентности всех систем отсчета. Разумеется, это не исключает того, что в одних системах отсчета и системах координат описание выглядит проще, а в других – сложнее. При переходе к динамике ситуация кардинально изменяется: достаточно универсальные законы можно получить лишь в так называемых инерциальных системах отсчета (ИСО), существование которых постулирует первый закон Ньютона, и в которых все свободные тела, т.е. тела не взаимодействующие с другими телами, движутся равномерно и прямолинейно или покоятся. Система отсчета связанная с Землей (геоцентрическая система отсчета) с достаточно высокой степенью точности инерциальна при изучении явлений, протекающих в небольших пространственных и временных масштабах, но для описания движения, например, планет она малопригодна и для этого используется система отсчета, связанная с Солнцем (гелиоцентрическая система отсчета), инерциальная в значительной бóльших пространственных и временных масштабах. В ИСО импульс частицы 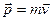может изменяться только в результате взаимодействия частицы с окружающими телами, и это изменение описывает второй закон Ньютона

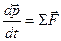. (1.40)

Каждая из сил, стоящих справа, является вектором, характеризующим взаимодействие рассматриваемого тела с окружающими телами, т.е., образно говоря, для каждой силы можно указать конкретное тело, являющееся источником этой силы. В механике принято силы делить на неконтактные (иначе говоря, силы, действующие на расстоянии) и контактные. Неконтактные силы – это сила всемирного тяготения, частным случаем которой является сила тяжести, сила Кулона, сила Лоренца. Контактные силы – это сила нормальной реакции силы трения и упругости, сила Архимеда. Если масса тела постоянна, уравнение (1.40) приобретает вид:

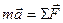. (1.41)

Векторную сумму сил называют равнодействующей: , и тогда (1.41) запишется в виде:

. (1.42)

Говорят, что задано состояние частицы, если известны F и 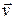, т.е. положение и скорость.

Силы, встречающиеся в природе, либо постоянны, либо зависят от координат и скорости тела, т.е. состояние частицы. Уравнение (1.40) или его частный случай (1.42) в динамике играют роль уравнений движения. Это означает, что задание начального состояния частицы: 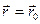, 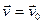при t=0, массы частицы и силы , действующей на частицу, позволяет найти положение частицы в любой момент времени t, используя указанные уравнения. Для одномерного движения рассмотрим три часто встречающихся случая.

1) Проекция силы 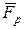на ось о 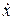, вдоль которой происходит движение, постоянна. Тогда при начальных условиях: при t=0, х=х₀, υ_х=υ_0х имеем

,

где С₁ – постоянная, определяемая из начальных условий: С₁= υ_0х, т.е. 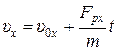. Далее, 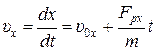, откуда . Интегрируя и используя начальное условие, получим зависимость хорошо известную из школьного курса

.

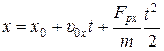2) Если F_рх зависит от координаты х по линейному закону F_х = F ₀+ bх, тогда удобно записать ускорение в виде . Иначе говоря, на первом этапе мы ищем зависимость скорости не от времени, а от координаты. Получим

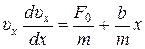, откуда .

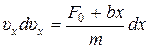Интегрируя и используя начальные условия, получим

.

Тогда

.

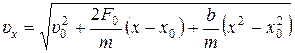Учитывая, что 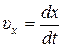, получим

.

Результат интегрирования зависит от знака b. При b >0 имеем

,

где , , .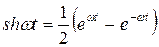

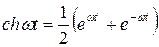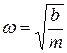При b <0 имеем в тех же обозначениях

, .

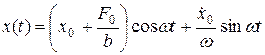Существенная разница между свойствами движения в этих случаях состоит в том, что первое из этих движений практически при любых начальных условиях сопровождается неограниченным возрастанием 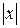при t®¥ (так называемые инфинитные движения), в то время как второе протекает в ограниченной области изменения координат (финитные движения или движения колебательного типа).

3) Если F_x зависит от скорости: , то полезной является та же замена, что и в предыдущем случае: 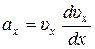и тогда

.

Интегрируя, если это возможно в элементарных функциях, получаем в неявном виде зависимость υ_х(х) и при повторном интегрировании (если оно возможно) и зависимость х=х(t). Конкретные примеры зависимости fυ_х будут рассмотрены в задаче 1. Второй закон Ньютона как уравнение движения должен быть дополнен законами для сил, т.е. уравнениями, определяющими силы через характеристики взаимодействующих тел. Типичными силами в механике являются: 1) сила тяжести , где g»9,8 м/с² – ускорение свободного падения вблизи поверхности Земли, при этом сила вследствие медленности вращения вокруг собственной оси практически перпендикулярна поверхности земли; 2) сила упругости, модуль которой равен 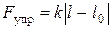, где k – коэффициент упругости пружины 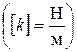, l – длина деформированной пружины, l ₀ – длина недеформированной пружины; направлена сила упругости, как известно, вдоль пружины, так, что пружина стремится возвратиться в недеформированное состояние; 3) сила взаимодействия двух точечных зарядов (сила Кулона), равная по модулю 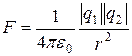, где 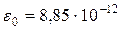Ф/м – электрическая постоянная, r – расстояние между зарядами; направлена сила Кулона по прямой, соединяющей заряды, и является силой отталкивания для одноименных зарядов и силой притяжения для разноименных; 4) силы взаимодействия твердых тел при контакте друг с другом – их называют силами реакции и представляют в виде суммы двух сил: касательной к границам раздела в точке соприкосновения, называемой силой трения 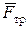и нормальной к указанной касательной силой 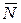, называемой силой нормальной реакции. При сухом трении, когда относительное проскальзывание в контакте отсутствует, имеем по закону Кулона-Амонтона F _тр£ kN (трение покоя), где k – коэффициент трения покоя, и сила 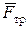препятствует относительному проскальзыванию, а при наличии проскальзывания говорят о силе трения скольжения, направленной против скорости данного тела относительно другого, находящегося с ним в контакте, и равной F _тр= mN, где m - коэффициент трения скольжения. Обычно m<k, но в большинстве случаев полагают безразмерные коэффициенты k и m одинаковыми: k=m. Если между соприкасающимися телами есть слой жидкости, или если тело просто движется в жидкости или газе, говорят о вязком (жидком) трении. Детали процесса очень сложны, но можно принять, что при небольших скоростях (разумеется, для каждой жидкости или газа и тела своя «небольшая» скорость) сила сопротивления (вязкого трения) пропорциональна первой степени скорости: 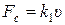, а при бóльших скоростях – второй степени скорости: .

Третий закон Ньютона для контактных взаимодействий гласит, что 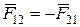, где 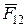– сила, действующая на тело 1 со стороны тела 2; 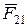– сила, действующая на тело 2 со стороны тела 1. По модулю, следовательно, эти силы равны, но направлены в противоположные стороны.

Для неконтактных взаимодействий, например для взаимодействия двух зарядов, к выписанному соотношению следует добавить, что силы направлены вдоль прямой, соединяющей частицы.

При взаимодействии нескольких частиц все силы взаимодействия можно разделить на внутренние и внешние. Внутренние силы – это силы взаимодействия частиц, входящих в рассматриваемую систему между собой, с внешние – это силы, действующие на частицы системы со стороны тел, которые в систему не входят. Если сумма внешних сил равна нулю, система называется изолированной или замкнутой. Для такой системы импульс системы, понимаемый как сумма импульсов отдельных частиц, с течением времени не изменяется:

, (1.43)

где 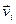– скорости тел в момент времени t₁, 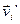– в момент времени t₂.

Формула (1.43) выражает закон сохранения импульса. Его обычно применяют в ситуациях, когда неизвестна детальная зависимость внутренних сил от времени и взаимных расположений тел. Для кратковременных взаимодействий тел типа ударов, выстрелов, взрывов и т.п. внутренние силы очень велики, и если при этом не происходит возрастание внешних сил из-за наличия опоры, то закон сохранения импульса в векторном виде (1.43) также справедлив с высокой точностью.

Распространены также ситуации, когда при рассматриваемых кратковременных взаимодействиях происходит резкое возрастание внешних сил. Типичный пример: ствол пушки наклонен под углом к горизонту и при выстреле происходит резкое возрастание силы нормальной реакции опоры и силы трения, если опора шероховатая. В этом случае закон сохранения импульса неприменим вообще, но если опора гладкая, т.е. сумма проекций внешних сил на ось х, направленную вдоль опоры, равна нулю, то сохраняется проекция импульса системы на указанную ось:

. (1.44)

Центр инерции (центр масс) системы (С) определяется как точка, радиус-вектор которой определяется формулой

,

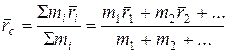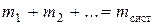где m_i – массы частиц, – их радиус-векторы, – масса системы. Дифференцируя эту формулу в предположении постоянства масс частиц, получим

,

т.е. импульс системы находится так, как будто вся масса системы сосредоточена в центре инерции. Используя второй закон Ньютона для системы частиц, получим уравнение движения центра инерции

,

т.е. центр инерции движется так, как будто в нем сосредоточена вся масса системы и к нему приложена сила, равная векторной сумме всех внешних сил, действующих на частицы системы. Согласно сказанному выше, несмотря на отсутствие внутренних сил в правой части уравнения, они могут, все-таки, влиять на движение центра инерции.

Элементарная работа силы 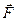по определению равна

,

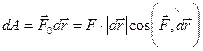а работа при конечном перемещении вдоль траектории L представляет собой криволинейный интеграл

.

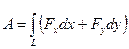Кинетической энергией системы называется величина

. (1.45)

Справедлива теорема о кинетической энергии системы:

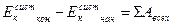, (1.46)

где слева стоит приращение кинетической энергии системы (разность между конечной и начальной кинетическими энергиями), а справа – сумма работ всех сил (как внешних, так и внутренних). При этом работа некоторых сил, которые называются консервативными, не зависит от форм траекторий тел, а определяется лишь их начальным и конечным положениями, а работа других сил, называемых неконсервативными, зависит от форм траекторий этих тел. Типичными консервативными силами в механике являются сила тяжести, работа которой равна

,

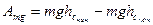где 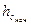и – начальная и конечная высоты центра масс тела соответственно над любой горизонтальной плоскостью (уровнем отсчета высот или нулевым уровнем), и сила упругости: если пружина с коэффициентом упругости k связывает два тела, то при любых их перемещениях суммарная работа сил упругости, действующих на оба тела равна

,

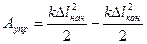где и – начальная и конечная деформации пружины.

Типичным примером неконсервативной силы является сила трения (сопротивления), работа которой для любого тела равна , где 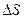– пройденный путь. Другим примером неконсервативной силы является так называемая сила тяги – сила, действующая на тело вследствие наличия на самом теле и связанных с ним телах работающего двигателя (например, сила тяги автомобиля, сила тяги, действующая на тело со стороны автомобиля и т.д.). Для консервативных сил можно ввести понятие потенциальной энергии. Для силы тяжести потенциальная энергия равна , где h_с – высота центра масс над любым уровнем для отсчета высот (нулевым уровнем). Для силы упругости 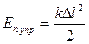, где D l – деформация пружины. Для некоторых консервативных сил, например, для силы Архимеда, вводить понятие потенциальной энергии не всегда удобно. Если тело движется вниз, то силу Архимеда можно считать силой сопротивления, а если вверх, то силой тяги. Сумма потенциальной и кинетической энергий называется полной механической энергией системы и тогда из (1.46) следует закон изменения механической энергии:

, (1.47)

где А_ост – работа остальных сил, для которых понятие потенциальной энергии либо не существует, либо она не фигурирует в левой части.

Если неконсервативные силы в системе отсутствуют, механическая энергия сохраняется:

. (1.48)

Законы (1.47) и (1.48) целесообразно применять в ситуациях, когда в задачах не требуется определять ускорения тел и времена их движения.

.

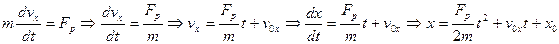В одномерном случае, когда , удобно произвести замену 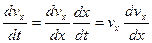. В этом случае имеем:

.

Если неопределенный интервал, стоящий справа, вычисляется в квадратурах, то константа интегрирования находится из условия 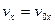при х=х₀. Иногда уравнение допускает дальнейшее интегрирование: , и в этом случае получается кинематический закон движения в неявном виде t=t(x). В случае, когда F_p=F_p(v_x) аналогично имеем:

,

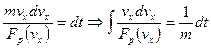и если интеграл, стоящий слева, берется в элементарных функциях, то после использования начальных условий получается зависимость t=t(v_x). Часто возможно дальнейшее интегрирование, конкретные варианты которого рассмотрены в примере решения задачи 1 контрольной работы.

Date: 2015-09-03; view: 442; Нарушение авторских прав