Общие теоремы динамики точки

Во многих инженерных задачах не требуется полного знания характеристик движения материальной точки. Отдельные, практически важные стороны явления могут быть изучены с помощью общих теорем, вытекающих из основного закона динамики. При этом широко используются такие характеристики движения, как количество движения, кинетическая энергия, импульс силы и другие. Дадим определения характеристик, которые нам потребуются в дальнейшем изложении.

Количеством движения материальной точки называется вектор q, равный произведению массы точки т на ее скорость v, т. е.

В физике количество движения часто называют импульсом материальной точки. Мы будем использовать оба эти названия. Вектор количества движения точки считается приложенным в самой движущейся точке.

Кинетической энергией точки называется скалярная величина Т, равная половине произведения массы точки на скалярный квадрат ее скорости:

Эту величину часто называют также живой силой.

Эффект действия силы на материальную точку зависит не только от величины силы, но и от продолжительности ее действия. Для характеристики действия, оказываемого силой за некоторый промежуток времени, вводится понятие импульса силы. Элементарным импульсом силы F называется векторная величина dS, равная произведению силы на элементарный промежуток времени dt:

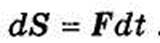
Как следует из определения, элементарный импульс направлен по линии действия силы. Суммируя элементарные импульсы, получим импульс силы за конечный промежуток времени t₁:

Если сила F в течение всего времени от 0 до t₁ остается постоянной и по модулю, и по направлению,

имеем S = Ft₁ а модуль импульса силы будет S = Ft₁. В общем случае модуль импульса силы может быть вычислен через его проекции. В частности, при использовании прямоугольной системы координат Oxyz проекции импульса силы F за промежуток времени от О до t₁ на координатные оси будут:

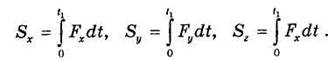
Энергетическими характеристиками действия силы при движении точки служат работа и мощность. Определим эти понятия. Пусть точка М (рис. 3.4) под действием силы F движется по траектории M₀M₁. Элементарной работой силы F называется скалярная величина dA, равная произведению проекции F_z силы F на касательную к траекториии направленную в сторону перемещения точки, на бесконечно малую дугу ds в направлении касательной, т. е.

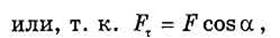
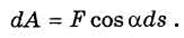
Если F_x, F_y, F_z – проекции силы F на декартовы оси х, у и z, a dx, dy, dz — проекции ds на те же оси, то формулу можно представить также в виде:

При конечном перемещении точки из положения M₀ в положение М₁ работа силы F вычисляется как интегральная сумма элементарных работ, т. е.

Мощностью N силы называется отношение элементарной работы dA к тому бесконечно малому промежутку времени dt, за который эта работа совершена, т. е.

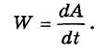
При неизменной во времени силе отсюда следует, что

где t₁ — время, в течение которого совершена работа А Используя формулу, можно получить:

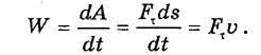
1. Теорема об изменении количества движения материальной точки. Пусть масса точки остается постоянной. Поскольку а — dv / dt, основной закон динамики точки, движущейся под действием п сил, можно представить в виде:

Формулы выражают теорему об изменении количества движения материальной точки в дифференциальной форме: производная по времени от количества движения точки равна векторной сумме действующих на точку сил.

Интегрируя вторую из формул (32.13) в пределах от t = 0 до t = t₁, получим:

Обозначим q(t₁) = q₁, q(0) = q₀. Найдем:

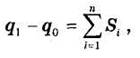
где S_i — импульс i-й силы за промежуток времени от 0 до t₁. Формула выражает теорему об изменении количества движения точки в конечном виде: изменение количества движения материальной точки за некоторый промежуток времени равно векторной сумме импульсов всех приложенных к точке сил за тот же промежуток времени.

Векторное равенство (32.14) в декартовых координатах представляется тремя скалярными выражениями:

В случае прямолинейного движения точки из трех равенств остается одно, а при движении по плоскости – только два.

2. Теорема об изменении кинетической энергии точки. Запишем основной закон динамики материальной точки в виде:

где F – равнодействующая сил, приложенных к точке. Умножим скалярно обе части этого соотношения на дифференциал радиус-вектора точки dr. Имеем:

Учитывая, что по определению dr/dt = v, получим:

Левую часть этого равенства можно представить в виде:

а скалярное произведение в его правой части представляет собой дифференциал работы dA силы F. В самом деле,

Таким образом, окончательно получим:

Формула в дифференциальной форме выражает теорему об изменении кинетической энергии материальной точки: дифференциал кинетической энергии точки равен элементарной работе приложенной к точке силы.

Разделим обе части равенства на dt. Тогда, учитывая, что dA / dt — N есть мощность силы F, получим другое выражение теоремы:

т. е. производная от кинетической энергии точки по времени равна мощности приложенной к точке силы.

Пусть в положении М₀ скорость точки равна v₀, а в положении М1 – v₁.

Интегрируя обе части равенства от точки М₀ до точки M₁, получим математическое выражение теоремы об изменении кинетической энергии точки в конечной форме:

т. е. изменение кинетической энергии точки на конечном перемещении равно работе силы, действующей на точку при том же перемещении.

3. Теорема об изменении момента количества движения точки. Количество движения q материальной точки есть векторная величина. Определим моменты этого вектора относительно центра и относительно оси.

Момент количества движения q = mv точки М относительно центра О (рис. 3.5а) есть вектор Lo, равный векторному произведению радиус-вектора г точки М, проведенного из. центра О, и вектора q:

Модуль вектора Lo равен произведению величины mv на плечо h вектора mv относительно центра О (рис. 3.5а):

Отсюда вытекает, что модуль L₀ равен удвоенной площади заштрихованного на рис. 3.5а треугольника с основанием mv и высотой h.

Моментом (L₀) количества движения (mv) материальной точки М относительно оси z (рис. 3.56) называется взятое со знаком плюс или минус произведение проекции (mv₁) вектора mv на плоскость а, перпендикулярную оси z, на плечо h₁ этой проекции относительно точки (О) пересечения оси z и плоскости a:

причем L_z > О, если с конца оси z вектор mv₁ виден направленным против вращения часовой стрелки, и L_z < 0 в противном случае.

Так же, как в статике, моменты количества движения относительно центра О и относительно оси z, проходящей через этот центр, связаны зависимостью:

Обозначая координаты движущейся точки М через х, у, z, а проекции скорости этой точки на оси координат через v_х, v_y, v_z, можно получить:

Докажем следующее предложение.

Теорема. Производная по времени от момента количества движения материальной точки относительно произвольно выбранного неподвижного центра равна векторной сумме моментов сил, действующих на точку, относительно того же центра.

Доказательство. Пусть точка М движется по траектории аb под действием силы Р. Выберем произвольный центр О и проведем из точки О радиус-вектор r в точку М. Момент силы Р относительно центра О будет:

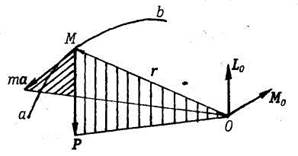
По формуле момент количества движения точки М относительно центра О определяется формулой:

Продифференцируем последнюю формулу по времени, учитывая при этом, что dr/dt = v и dv/dt = a. Получим:

Так как векторы v и mv коллинеарные, их векторное произведение равно нулю. Поэтому:

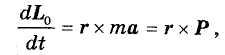
или

При действии на материальную точку нескольких сил (P₁, Р₂,..., Р_n) момент М_о равнодействующей Р

равен векторной сумме моментов составляющих сил, и формула принимает вид:

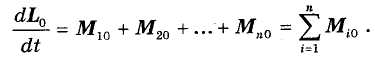
Теорема доказана. Проектируя векторное равенство на оси х, у, г, можем записать:

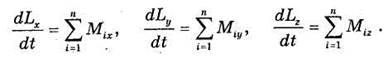
Следствие 1. Если равнодействующая всех сил, приложенных к материальной точке, проходит через некоторый неподвижный центр, то момент количества движения точки относительно этого центра остается постоянным.

В самом деле, если равнодействующая Р проходит через центр О, то М_о = 0, и по формуле (32.23):

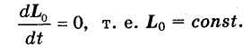
Следствие 2. Если момент равнодействующей всех сил, приложенных к материальной точке, относительно некоторой оси равен нулю, то момент количества движения точки относительно этой оси остается постоянным.

Из соотношений следует, что если, например,

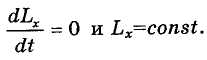
ДИНАМИЧЕСКАЯ ТЕОРЕМА КОРИОЛИСА

Пусть материальная точка массы т перемещается в подвижной, в общем случае неинерционной системе отсчета Охуz (рис. 3.2). Введем инерциальную систему отсчета Ox₁y₁z₁. Равнодействующую приложенных к точке активных сил обозначим через F, а равнодействующую сил реакций связей – через N. В инерциальной системе отсчета Ox₁y₁z₁ уравнение движения точки в векторной форме будет:

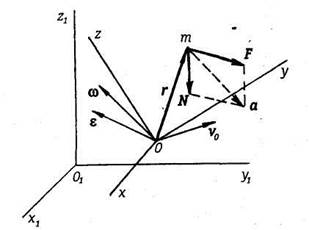
причем а – абсолютное ускорение точки. Применяя теорему о сложении ускорений, имеем:

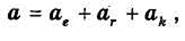
где а_е, а_r, а_к – соответственно переносное, относительное и кориолисово ускорения точки. Подставляя абсолютное ускорение а по формуле в уравнение движения, получим:

Силы Фе и Фк, определяемые формулами, называются соответственно переносной и кориолисовой силами инерции.

Формула, представляющая уравнение относительного движения точки в векторной форме, выражает динамическую теорему Кориолиса: материальная точка движется относительно неинерциальной системы отсчета так же, как и относительно инерциальной, только к приложенным активным силам и реакциям связей следует добавить переносную и кориолисову силы инерции.

Силы инерции Фе и Фк являются поправками на неинерциальностъ системы отсчета. Если подвижная система отсчета Охуг движется относительно основной инерциальной системы поступательно, равномерно и прямолинейно (w = 0, e = 0), то силы инерции Фе, Фк обращаются в нуль. В этом случае уравнение относительного движения точки (31.3) принимает вид:

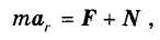
|что совпадает с уравнением движения относительно инерциальной системы отсчета. Полученный результат отражает принцип относительности классической механики — принцип Галилея-Ньютона, который можно сформулировать в виде: все механические явления в различных инерциалъных системах отсчета протекают одинаково, или никакими механическими опытами нельзя обнаружить инерциалъное движение системы отсчета, участвуя вместе с ней в этом движении.

ДИНАМИКА СИСТЕМЫ

Date: 2015-09-03; view: 1183; Нарушение авторских прав