Св-ва осевой сим-ии

Опр. Точка Р наз-ся неподвижной точкой преобраз-я f, если f(P) = Р, т. е. образ точки Р совпадает с этой точкой.

1°. Осевая сим-ия имеет бесконечное мн-во неподвижных точек - это ось сим-ии.

2°. Осевая сим-ия всякую прямую, перпендик-ю оси сим-ии, отобр-ет на себя.

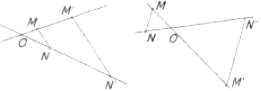
3°. Если прямая а пересекает ось сим-ии в точке К, то сим-ичная ей прямая a` пересекает ось сим-ии в той же точке К, при этом образует с осью угол, равный углу м/у прямой а и осью (рис. 1).

4°. Если прямая а парал-на оси сим-ии, то симметр-я ей прямая а' тоже параллельна оси сим-ии, при этом она отстоит от оси на таком же расстоянии, что и прямая а (рис. 2).

5°. Осевая сим-ия отобр-ет окр-ть в равную ей окр-ть,

6°. Если центр окр-ти принадлежит оси сим-ии, то окружность сим-ична самой себе.

Опр. Прямая l наз-ся осью сим-ии фигуры Ф, если осевая сим-ия S_l, отобр-ет эту фигуру на себя.

7°. Каждая прямая l, проходящая ч/з центр О окр-ти, явл-ся осью сим-ия этой окр-ти.

8°Всякая паря пересек-ся прямых имеет две оси сим-ии - это прямые, делящие пополам углы м/у прямыми.

9°Всякая пара парал-х прямых имеет одну ось сим-ии - это прямая, парал-я данным прямым и равноотстоящая от них.

Параллельный перенос пл-ти

Опр. Парал-ным переносом пл-ти, обознач-м 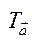, на в-тор 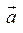, наз-ся преобраз-е пл-ти, к-рое каждой точке М ставит в соотв-е точку М' по закону: = .

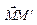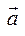Т. Парал-ный перенос пл-ти есть движ-е.

Сл-е. Парал-й перенос пл-ти обладает всеми св-ми движ-я, в частности: прямую отобр-ет в прямую, парал-ные прямые - в парал-ные прямые, окр-ть - в равную ей окр-ть, сохраняет расст-я и углы.

Св-ва парал-го переноса.(ПП)

1°. ПП (на ненулевой вектор) не имеет неподвижных точек.

2°. ПП отображает прямую, параллельную вектору переноса, в себя.

3°. ПП отобр-ет прямую, не парал-ю в-ру переноса, в парал-ю ей прямую.

4°Любую из 2-х равных окр-тей можно отобр-ть в др-ю окр-ть парал-м переносом на в-тор, соед-щий центры данных окр-тей.

Поворот пл-ти

Опр. Углом м/у в-рам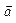и и наз-ся угол м/у лучами ОА и ОВ такими, что в-ры = , = .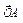

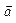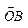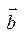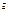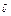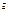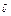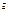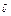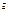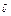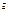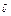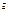
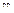
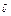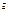
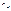
Опр. Ориентированным (направленным) углом м/у в-рами и на ориентир-й пл-ти наз-ся угол м/у в-рами и , если базис { , } - правый, и угол м/у в-рами и , взятый со знаком "-", если базис { , } - левый. Если в-ры , то ориент-ный угол м/у ними считается равным 0, а если 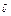то - π

Обозн. 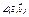-ориент-ный угол м/у в-рам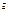и и .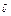

Опр. Поворотом пл-ти, обознач-м R^φ_O, с центром поворота О и углом поворота φ наз-ся преобраз-е пл-ти, к-рое каждой точке М ставит в соотв-е точку М' по закону:

1. ОМ = ОМ'

2 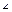MOM'=φ (ориент-й угол)

Ф-лы поворота.

x'=хcosφ-уsinφ,

у'=xsinφ+уcosφ. (4)

Т. Поворот пл-ти явл-ся движ-ем.

Сл-е. Поворот пл-ти обладает всеми св-ми движ-я, в частности: прямую отобр-ет в прямую, парал-е прямые — в парал-е прямые, окр-ть — в равную ей окр-ть, сохраняет расстояния и углы.

Характерные св-ва поворота.

1°. Поворот пл-ти имеет одну неподв-ю точку -центр поворота.

2°. При повороте пл-ти угол м/у прямой и ее образом равен углу поворота.

Центральная сим-ия пл-ти.

Опр. Центральной сим-ией Z_o пл-ти с центром сим-ии О наз-ся преобраз-е пл-ти, к-рое каждой т. М ставит в соотв-е т. М' по закону: М' ОМ; ОМ = ОМ', М и М' лежат по разные стороны от точки О. Из опр-я следует, что Z₀ = 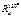, т. е. центральная сим-ия является поворотом на 180°.

Ф-лы цен-ая сим-ия: х'=-х, у'=-у (5)

Верно и обратное утвержд-е: если преобраз-е пл-ти задано ф-ми (5), то оно явл-ся центральной сим-ией. Т.о., ф-лы (5) есть ф-лы центр-й сим-ии с центром в начале корд-т.

Если центр сим-ии лежит в точке S(x_o,y_o), то ф-лы центральной сим-ии принимают вид: х'-х₀= -(х-х₀), у'-y₀=-(у-у_о) (6)

Т. Центральная сим-ия пл-ти явл-ся движ-ем.

Следствие. Центральная сим-ия обладает всеми св-ми движ-я, в частности.

Св-ва центральной сим-ии.

1°. Центральная сим-ия имеет 1 неподв-ю точку - центр сим-ии.

2°. Центральная сим-ия отобр-ет всякую прямую, проходящую ч/з центр сим-ии, на себя,

3°. Центральная сим-ия отобр-т всякую прямую, не проходящую ч/з центр сим-ии, на парал-ю ей прямую.

4°. Окр-ть центрально-сим-ична самой себе относ-но своего центра.

5°. Для любых 2-х равных окр-тей сущ-ет центральная сим-ия, отобр-щая одну окр-ть на другую. Центром сим-ии явл-ся середина отрезка, соед-го центры окр-тей.

Скользящая сим-ия пл-ти

Опр. Скользящей сим-ией 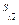, пл-ти наз-ся композиция парал-го переноса T и осевой сим-ии S_l, при этом вектор 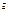|| l. Т.о., по опр-ю = S_loT

Ф-лы скользящей сим-ии

х'=х+а₁, y`=-y (7)

Т. Скользящая сим-ия пл-ти есть движ-е второго рода.

Преобраз-е подобия (пр под) пл-ти

Опр. Пусть имеются 2 ПДСК 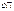, , 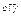| |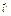=| |= k | 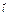|= k | 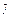|= k, k>0, тогда преобраз-е пл-ти к-рой каждой точке М(х.у) относ-но 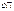ставит в соотв-и точку М` (х.у) относ-но 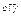наз-ся преобраз-ем подобия пл-ти с кoоэф подобия k.

Св-ва преобраз-я подобия.

1° Пр. под. пл-ти всякую прямую отобр-т в прямую.

2°.Пр. под. пл-ти отображает полупл-сть с границей l в полупл-ть с границей l', где l`=f(l).

4°. Пр. под. пл-ти сохраняет отнош-е "лежать между".

5°. Пр. под. пл-ти отобр-ет отрезок в отрезок, луч в луч.

6°. Пр. под. пл-ти отобр-ет угол в равный ему угол.

7°. Пр. под. пл-ти отобр-ет парал-е прямые в парал-е прямые.

Сл-е. Пр. под. пл-ти отобр-ет параллелограмм в параллелограмм.

8°. Пр. под. пл-ти отобр-ет вектор в в-тор, сумму в-ров в сумму ве-ров и произв-е числа на в-тор в произвед-е того же числа на соотв-щий вектор.

Т. Если преобраз-е пл-ти изменяет расстояние м/у любыми 2мя точками в одном и том же отношении, равном k>0, то оно явл-ся преобраз-ем подобия с коэфф-м подобия k.

Опр. Пр. под. пл-ти с коэфф-м подобия k>0 наз-ся преобраз-е пл-ти, изменяющее расстояние м/у любыми 2мя точками в одном и том же отнош-и, равном k.

Опр. Гомотетией пл-ти с центром гомотетии О и коэфф-м гомотетии k≠0 наз-ся преобраз-е пл-ти, к-рое всякой точке М пл-ти ставит в соотв-е точку М' по закону: 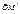= k (9)

k>0 k<0

Обозн. H_o^k - гом-я пл-ти с центром гом-тии О и коэфф-м гом-тии k.

Опр. Гомот-ми фигурами наз-ся фигуры Ф и Ф'=H_o^k(Ф).

1)Гомотет-е точки М и М ‘ лежат на одной прямой с центром гом-тии О. 2)Точки М и М' лежат по одну сторону от центра О, если k>0, и - по разные стороны, если k<0. 3) ОМ`=|k|*ОМ.

4) Гом-тия пл-ти явл-ся при: k= 1 – тожд-ным преобраз-м; k=- 1 - центральной сим-ией.

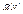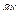Осн-е св-во гом-тии: Для любых точек М, N и их образов М', N' имеет место рав-во: вектора =k (10)

Св-ва гом-тии,

1°. Гом-тия пл-ти имеет одну неподв-ю точку — центр гом-тии

2°. Гом-тия пл-ти отобр-ет прямую, проходящую ч/з центр гом-тии, в себя. Иначе говоря, прямая, проходящая ч/з центр гом-тии, гомотетична самой себе.

3°. Гом-тия пл-ти (k ≠1) отобр-ет прямую, не проходящую ч/з центр гом-тии, в парал-ю ей прямую, также не проходящую ч/з центр гом-тии. Иначе говоря, гом-ные прямые парал-ны.

4°. Гом-тия пл-ти отобр-ет окр-ть, центр к-рой совпадает с центром гом-тии, в концентрическую окр-ть, при этом радиусы окр-тей связаны соотнош-ем r'=|k|r.

5°. Всякие две неравные окр-ти гомот-ны друг другу, при этом, если окр-ти не явл-ся концентрич-ми, сущ-т две гом-тии, отображ-е одну из них в другую.

Аффинное преобраз-е пл-ти

Опр. Пусть имеются 2 аффинные с-мы корд-т (АСК) 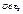и 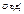.Тогда преобраз-е пл-ти, к-рое каждой точке М с корд-ми (х,у) относ-но 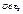ставит в соотв-е точку М' с теми же корд-ми (х,у), но относ-но 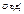, наз-ся аффинным преобраз-ем, пл-ти.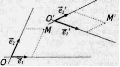

Из опр-ия следует, что движ-е и пр. под. пл-ти явл-ся аффинными преобраз-ми.

Св-ва аффинного преобраз-я.

1° Аф. преобраз-е пл-ти всякую прямую отображает в прямую.

2°. Аф. преобраз-е пл-ти отобр-ет полупл-ть с границей l в полупл-ть с границей l', где l` = f(l).

3°. Аф. преобраз-е пл-ти сохраняет отношение "лежать между".

4°, Аф. преобраз-е пл-ти отобр-т отрезок в отрезок, луч в луч.

5°. Аф. преобраз-е пл-ти отобр-ет парал-е прямые в парал-е прямые.

Сл-е. Аф-е преобраз-е пл-ти отобр-ет параллелограмм в парал-м

6°. Аф. преобр-е пл-ти отобр-ет в-тор в в-тор, сумму в-ров в сумму в-ров и произв-е числа на в-тор в произв-е того же числа на соотв-щий в-тор.

7°. Аф. преобр-е пл-ти сохраняет отнош-е отрезков, лежащих на одной или парал-х прямых.

Т. (О задании аф-го преобр-я). Пусть А, В, С и А', В', С` — любые две тройки некол-ных точек. Тогда сущ-ет одно и только одно аф-е преобр-е пл-ти, отобр-щее А в А', В в В', С в С`.