
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Тема 6. Выборочное наблюдение
Выборочное наблюдение – такой вид несплошного наблюдения, при котором статистическому обследованию подвергается часть единиц изучаемой совокупности, отобранных в случайном порядке, а обобщающие показатели, рассчитанные по этой части распространяются затем на всю совокупность.
В процессе выборочного наблюдения статистика выделяет два вида ошибок: ошибки регистрации; ошибки репрезентативности – возникают в силу того, что выборочная совокупность не полностью воспроизводит генеральную.
Ошибки регистрации и репрезентативности могут иметь случайный (непреднамеренный) или систематический (тенденциозный) характер.
Ошибка выборочного наблюдения – разность между величиной параметра в генеральной совокупности и его величиной, вычисленной по результатам выборочного наблюдения.
Средняя ошибка выборки для средней показывает среднюю величину всех возможных расхождений выборочной и генеральной средней.
Главными вопросами теории выборочного наблюдения являются:
· определение предела случайной ошибки репрезентативности с учетом особенностей отбора;
· определение оптимального объема выборки
Предельная ошибка выборки (D) для среднего показателя определяется при повторном способе отбора по формуле: 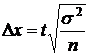 ; для доли
; для доли 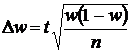 .
.
При бесповоротном способе отбора предельная ошибка:
для средней 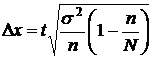
для доли 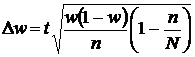
где t – коэффициент кратности средней ошибки выборки, зависящий от вероятности, с которой гарантируется величина предельной ошибки;
В качестве уровня гарантийной вероятности обычно берут:
P = 0,954, тогда t = 2; P = 0,997, тогда t = 3;
s 2 – дисперсия среднего показателя;
w (1 – w) – дисперсия доли альтернативного показателя; n – объем выборочной совокупности; N – объем генеральной совокупности.
Определение ошибок выборочных совокупностей позволяет установить границы нахождения соответствующих генеральных показателей:
для средней 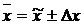 ; для доли
; для доли 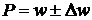 ,
,
где 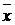 - генеральная средняя; х – выборочная средняя;
- генеральная средняя; х – выборочная средняя; 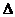 х – ошибка выборочной средней; Р – генеральная доля; w – выборочная доля;
х – ошибка выборочной средней; Р – генеральная доля; w – выборочная доля;  w – ошибки выборочной доли.
w – ошибки выборочной доли.
Для определения численности выборки (n) используют формулу для среднего показателя
 , а для доли
, а для доли 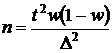 .
.
При бесповторном способе отбора необходимая численность выборки для среднего показателя определяется по формуле:
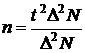 , а для доли
, а для доли 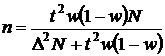 .
.
Решение типовых примеров
Пример 1
Для изучения стажа торговых работников была проведена 5%-ная механическая выборка. Результаты обследования показали следующее распределение работников торговли, представленное в табл. 1.
Таблица 1 - Распределение работников торговли по стажу работы
| Стаж, лет | Число работников прилавка, чел |
| до 6 | |
| 6 - 12 | |
| 12 - 18 | |
| 18 - 24 | |
| св. 24 | |
| ИТОГО |
На основании этих данных исчислить вероятностью 0,997 возможные пределы, в которых ожидается средняя заработная плата работников торговли.
Средний стаж работников торговли определим по формуле средней арифметической взвешенной:
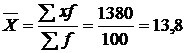 года.
года.
Дисперсия: 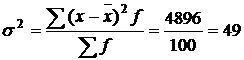 (лет).
(лет).
Среднее квадратическое отклонение исчислим по формуле:
 (лет)
(лет)
Предельная ошибка рассчитывается по формуле: 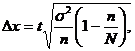 где
где
s2 - дисперсия выборочной совокупности; n - число единиц выборочной совокупности; N - число единиц генеральной совокупности.
Показатели, рассчитанные выше, относятся к выборочной совокупности:
s 2= 49 лет; n = 100 рабочих; 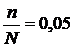 (доля отбора 5 % по условию),
(доля отбора 5 % по условию),
Р = 0997; t = 3.
Следовательно, 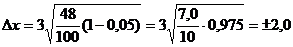 года.
года.
Предельная ошибка выборки показывает наибольшее отклонение выборочной средней 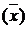 от генеральной средней (
от генеральной средней (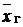 ), которое можно гарантировать с заданной вероятностью:
), которое можно гарантировать с заданной вероятностью:
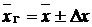 или
или 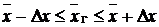 .
.
Пределы средней зарплаты во всей совокупности работников торговли равны:
13,8 года ± 2 года; 11,8 года < 13,8 < 15,8 года
С вероятностью 0,997 можно утверждать, что средний стаж работников во всей совокупности будет колебаться от 11,8 до 15,8 года.
Тесты
1.Расхождение междузафиксированным при наблюдении значением признака и действительным его значением называется:
а) ошибкой репрезентативности; б) ошибкой регистрации;
в) средней ошибкой выборки; г) предельной ошибкой выборки.
2. Расхождение между величинами выборных и соответствующих генеральных показателей называется:
а) ошибкой репрезентативности; б) ошибкой регистрации;
в) средней ошибкой выборки; г) предельной ошибкой выборки.
3. Если ту или иную единицу, попавшую в выборку, после регистрации изучаемого признака снова возвращают в генеральную совокупность, и она сохраняет равную возможность со всеми прочими единицами при повторном отборе единиц вновь попасть в выборку, то используется метод отбора:
а) индивидуальный; б) повторный; в) бесповторный;
г) случайный; д) механический.
4. Если ту или иную единица, попавшую в выборку, после регистрации изучаемого признака вновь в генеральную совокупность не возвращается и в дальнейшем в выборке не участвует, то используется метод отбора:
а) альтернативный; б) повторный; в) бесповторный;
г) случайный; д) индивидуальный.
5. Средняя ошибка выборки зависит:
а) от объема генеральной совокупности;
б) от степени варьирования признака;
в) от вероятности, с которой определяются границы показателей выборочной совокупности;
г) от объема выборочной совокупности;
 д) от способа отбора единиц в выборочную совокупность
д) от способа отбора единиц в выборочную совокупность
6. По формуле рассчитывается:
а) предельная ошибка выборки выборочной доли при бесповторном отборе;
б) средняя ошибка выборки выборочной средней при повторном отборе;
в) средняя ошибка выборки выборочной средней при бесповторном отборе;
г) предельная ошибка выборки выборочной доли при повторном отборе;
1) а; 2) б; 3) в; 4) г
7. Какая ошибка выборки рассчитывается по формуле:
 t . . (1 -)
t . . (1 -)
а) средняя ошибка выборки выборочной доли при бесповторном отборе;
б) предельная ошибка выборки выборочной средней при повторном отборе;
в) средняя ошибка выборки выборочной средней при бесповторном отборе;
г) предельная ошибка выборки выборочной доли при бесповторном отборе;
1) а; 2) б; 3) в; 4) г
 8. Какая ошибка выборки рассчитывается по формуле:
8. Какая ошибка выборки рассчитывается по формуле:
. (1 -)
а) предельная ошибка выборки выборочной доли при бесповторном отборе;
б) средняя ошибка выборки выборочной средней при повторном отборе;
в) средняя ошибка выборки выборочной средней при бесповторном отборе;
г) предельная ошибка выборки выборочной доли при повторном отборе;
1) а; 2) б; 3) в; 4) г
9. Недостающим элементом формулы средней ошибки выборки для доли при бесповторном отборе является:
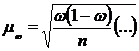
1) (1-n/N); 4) S2 ;
2) (N-1); 5)  ;
;
3) 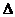 ; 6)
; 6) 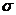
10. Как изменится численность выборочной совокупности, если вероятность, гарантирующую результат выборочного наблюдения, увеличить с 0,954 (t = 2) до 0,997 (t = 3).
1) увеличится на единицу;
2) увеличится на пять единиц;
3) не изменится;
4) результат предсказать невозможно.
11. Как изменится численность выборочной совокупности, если вероятность, гарантирующую результат выборочного наблюдения, уменьшить с 0,997 (t = 3) до 0,954 (t = 2).
1) увеличится на единицу;
2) увеличится на пять единиц;
3) не изменится;
4) результат предсказать невозможно
12. Как изменится средняя ошибка случайной повторной выборки, если её объем увеличить в четыре раза
1) уменьшится в 4 раза
2) не изменится
3) увеличится в 4 раза
4) уменьшится в 2 раза
13. Как изменится средняя ошибка случайной повторной выборки, если её объем уменьшить в четыре раза
1) уменьшится в 4 раза
2) не изменится
3) увеличится в 2 раза
4) уменьшится в 2 раза
14. Каким образом необходимо изменить численность выборочной совокупности, чтобы средняя ошибка повторной выборки уменьшилась в два раза
1) уменьшить в 4 раза
2) увеличить в 4 раза
3) увеличить в 2 раза
4) уменьшить в 2 раза
15. Каким образом необходимо изменить численность выборочной совокупности, чтобы средняя ошибка повторной выборки уменьшилась в три раза
1) уменьшить в 9 раз
2) увеличить в 9 раз
3) увеличить в 3 раза
4) уменьшить в 3 раза
16. Как изменится предельная ошибка повторной выборки, проведенной с вероятностью 0,997 (t=3), если численность выборочной совокупности увеличить в четыре раза?
1) увеличится в четыре раза;
2) увеличится в два раза;
3) уменьшится в четыре раза;
4) уменьшится в два раза.
17. Как изменится предельная ошибка повторной выборки, проведенной с вероятностью 0,997 (t=3), если численность выборочной совокупности уменьшить в четыре раза?
1) увеличится в четыре раза;
2) увеличится в два раза;
3) увеличится в два раза;
4) уменьшится в два раза.
18. Проведено бесповторное выборочное обследование заработной платы рабочих двух предприятий. Обследовано одинаковое число рабочих. Дисперсия заработной платы рабочих на обоих предприятиях одинакова, а общая численность рабочих больше на втором предприятии. Средняя ошибка выборки:
1) больше на первом предприятии;
2) больше на втором предприятии;
3) на обоих предприятиях одинакова;
4) данные не позволяют сделать вывод.
19. В результате бесповторного выборочного обследования одинакового числа работников двух туристических агенств установлено: дисперсия средней заработной платы сотрудников первого туристического агенства – 225 руб., а второго – 100 руб. Численность сотрудников первого туристического агенства в два раза больше, чем второго. Средняя ошибка выборки:
1) больше в первом туристическом агенстве;
2) больше во втором туристическом агенстве;
3) ошибки одинаковы;
4) предсказать результат невозможно.
20. Проведено бесповторное выборочное обследование производительности труда рабочих двух предприятий. Обследовано одинаковое число рабочих. Дисперсия производительности труда рабочих больше на первом предприятии, а общая численность рабочих на обоих предприятиях одинакова. Средняя ошибка выборки:
1) больше на первом предприятии;
2) больше на втором предприятии;
3) на обоих завода одинакова;
4) данные не позволяют сделать вывод.
Date: 2015-07-27; view: 3336; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |