Пара преобразований Фурье. Спектральная плотность сигнала

Пусть сигнал s (t) задан в виде непериодической функции, причем он существует только на интервале (t ₁ , t ₂) (пример - одиночный импульс). Выберем произвольный отрезок времени T, включающий в себя интервал (t ₁ , t ₂) (см. рис.1).

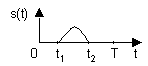
Рис. 1

Обозначим периодический сигнал, полученный из s (t), в виде s_T (t). Тогда для него можно записать ряд Фурье

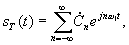
где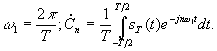

Подставим выражение для 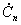в ряд:

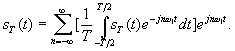
Для того, чтобы перейти к функции s (t) следует в выражении s_T (t) устремить период к бесконечности. При этом число гармонических составляющих с частотами w = n 2 p / T будет бесконечно велико, расстояние между ними будет стремиться к нулю (к бесконечно малой величине: 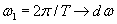, амплитуды составляющих также будут бесконечно малы. Поэтому говорить о спектре такого сигнала уже нельзя, т.к. спектр становится сплошным.

При предельном переходе в случае Т => 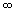, имеем:

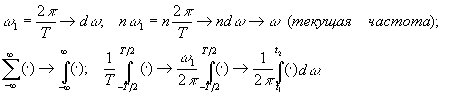
Таким образом, в пределе получаем

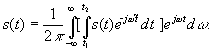
Внутренний интеграл является функцией частоты. Его называют спектральной плотностью сигнала, или частотной характеристикой сигнала и обозначают ,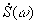

т.е.

(*)

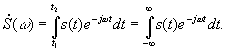
Пределы интегрирования можно для общности поставить бесконечными, так как все равно там, где s (t) равна нулю, и интеграл равен нулю.

Выражение для спектральной плотности называют прямым преобразованием Фурье. Обратное преобразование Фурье определяет временную функцию сигнала по его спектральной плотности:

(**)

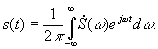
рямое (*) и обратное (**) преобразования Фурье вместе называют парой преобразований Фурье. Модуль спектральной плотности 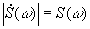определяет амплитудно-частотную характеристику (АЧХ) сигнала, а ее аргумент 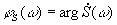называют фазо-частотной характеристикой (ФЧХ) сигнала. АЧХ сигнала является четной функцией, а ФЧХ - нечетной.

Смысл модуля S (w) определяется как амплитуда сигнала (тока или напряжения), приходящаяся на 1 Гц в бесконечно узкой полосе частот, которая включает в себя рассматриваемую частоту w. Его размерность - [сигнал/частота].

9. Свойства преобразования Фурье. Свойства линейности, изменения масштаба времени, другие. Теореме о спектре производной. Теорема о спектре интеграла.

10. Дискретное преобразование Фурье. Помехи радиоприёму. Классификация помех.

Дискретное преобразование Фурье может быть получено непосредственно из интегрального преобразования дискретизаций аргументов (t_k = kDt, f_n = nDf):

S(f) = 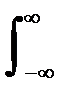s(t) exp(-j2pft) dt, S(f_n) = Dt 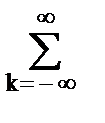s(t_k) exp(-j2pf_nkDt), (6.1.1)

s(t) = 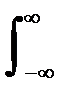S(f) exp(j2pft) df, s(t_k) = Df 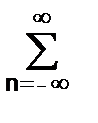S(f_n) exp(j2pnDft_k). (6.1.2)

Напомним, что дискретизация функции по времени приводит к периодизации ее спектра, а дискретизация спектра по частоте - к периодизации функции. Не следует также забывать, что значения (6.1.1) числового ряда S(f_n) являются дискретизаций непрерывной функции S'(f) спектра дискретной функции s(t_k), равно как и значения (6.1.2) числового ряда s(t_k) являются дискретизацией непрерывной функции s'(t), и при восстановлении этих непрерывных функций S'(f) и s'(t) по их дискретным отсчетам соответствие S'(f) = S(f) и s'(t) = s(t) гарантировано только при выполнении теоремы Котельникова-Шеннона.

Для дискретных преобразований s(kDt) Û S(nDf), и функция, и ее спектр дискретны и периодичны, а числовые массивы их представления соответствуют заданию на главных периодах Т = NDt (от 0 до Т или от -Т/2 до Т/2), и 2f_N = NDf (от -f_N до f_N), где N – количество отсчетов, при этом:

Df = 1/T = 1/(NDt), Dt = 1/2f_N = 1/(NDf), DtDf = 1/N, N = 2Tf_N. (6.1.3)

Соотношения (6.1.3) являются условиями информационной равноценности динамической и частотной форм представления дискретных сигналов. Другими словами: число отсчетов функции и ее спектра должны быть одинаковыми. Но каждый отсчет комплексного спектра представляется двумя вещественными числами и, соответственно, число отсчетов комплексного спектра в 2 раза больше отсчетов функции? Это так. Однако представление спектра в комплексной форме - не более чем удобное математическое представление спектральной функции, реальные отсчеты которой образуются сложением двух сопряженных комплексных отсчетов, а полная информация о спектре функции в комплексной форме заключена только в одной его половине - отсчетах действительной и мнимой части комплексных чисел в частотном интервале от 0 до f_N, т.к. информация второй половины диапазона от 0 до -f_N является сопряженной с первой половиной и никакой дополнительной информации не несет.

При дискретном представлении сигналов аргумент t_k обычно проставляется номерами отсчетов k (по умолчанию Dt = 1, k = 0,1,…N-1), а преобразования Фурье выполняются по аргументу n (номер шага по частоте) на главных периодах. При значениях N, кратных 2:

S(f_n) º S_n = 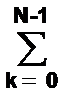s_k exp(-j2pkn/N), n = -N/2,…,0,…,N/2. (6.1.4)

s(t_k) º s_k = (1/N) 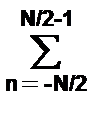S_n exp(j2pkn/N), k = 0,1,…,N-1. (6.1.5)

Главный период спектра в (6.1.4) для циклических частот от -0.5 до 0.5, для угловых частот от -p до p. При нечетном значении N границы главного периода по частоте (значения ±f_N) находятся на половину шага по частоте за отсчетами ±(N/2) и, соответственно, верхний предел суммирования в (6.1.5) устанавливается равным N/2.

В вычислительных операциях на ЭВМ для исключения отрицательных частотных аргументов (отрицательных значений номеров n) и использования идентичных алгоритмов прямого и обратного преобразования Фурье главный период спектра обычно принимается в интервале от 0 до 2f_N (0 £ n £ N), а суммирование в (6.1.5) производится соответственно от 0 до N-1. При этом следует учитывать, что комплексно сопряженным отсчетам S_n* интервала (-N,0) двустороннего спектра в интервале 0-2f_N соответствуют отсчеты S_N+1-n (т.е. сопряженными отсчетами в интервале 0-2f_N являются отсчеты S_n и S_N+1-n).

Пример: На интервале Т= [0,99], N=100, задан дискретный сигнал s(k) = 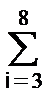d(k-i) - прямоугольный импульс с единичными значениями на точках k от 3 до 8. Форма сигнала и модуль его спектра в главном частотном диапазоне, вычисленного по формуле S(n) = 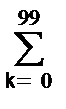s(k)×exp(-j2pkn/100) с нумерацией по n от -50 до +50 с шагом по частоте, соответственно, Dw=2p/100, приведены на рис. 6.1.1.

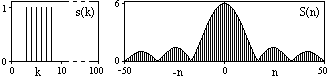
Рис. 6.1.1. Дискретный сигнал и модуль его спектра.

На рис. 6.1.2 приведена огибающая значений другой формы представления главного диапазона спектра. Независимо от формы представления спектр периодичен, в чем нетрудно убедиться, если вычислить значения спектра для большего интервала аргумента n с сохранением того же шага по частоте, как это показано на рис. 6.1.3 для огибающей значений спектра.

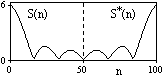
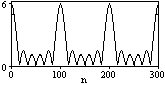
Рис. 6.1.2. Модуль спектра. Рис. 6.1.3. Модуль спектра.

На рис. 6.1.4. показано обратное преобразование Фурье для дискретного спектра, выполненное по формуле s'(k) =(1/100) 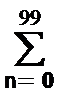S(n)×exp(j2pkn/100), которое показывает периодизацию исходной функции s(k), но главный период k={0,99} этой функции полностью совпадает с исходным сигналом s(k).

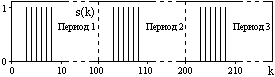
Рис. 6.1.4. Обратное преобразование Фурье.

Преобразования (6.1.4-6.1.5) называют дискретными преобразованиями Фурье (ДПФ). Для ДПФ, в принципе, справедливы все свойства интегральных преобразований Фурье, однако при этом следует учитывать периодичность дискретных функций и спектров. Произведению спектров двух дискретных функций (при выполнении каких-либо операций при обработке сигналов в частотном представлении, как, например, фильтрации сигналов непосредственно в частотной форме) будет соответствовать свертка периодизированных функций во временном представлении (и наоборот). Такая свертка называется циклической (см. раздел 6.4) и ее результаты на концевых участках информационных интервалов могут существенно отличаться от свертки финитных дискретных функций (линейной свертки).

Из выражений ДПФ можно видеть, что для вычисления каждой гармоники нужно N операций комплексного умножения и сложения и соответственно N² операций на полное выполнение ДПФ. При больших объемах массивов данных это может приводить к существенным временным затратам. Ускорение вычислений достигается при использовании быстрого преобразования Фурье.

Помехи

Помехами обычно называют посторонние электрические возмущения, накладывающиеся на передаваемый сигнал и затрудняющие его прием. При большой интенсивности помех прием становится практически невозможным.

Классификация помех:

а) помехи от соседних радиопередатчиков (станций);

б) помехи от промышленных установок;

в) атмосферные помехи (грозы, осадки);

г) помехи, обусловленные прохождением электромагнитных волн через слои атмосферы: тропосферу, ионосферу;

д) тепловые и дробовые шумы в элементах радиоцепей, обусловленные тепловым движением электронов.

Математически сигнал на входе приемника можно представить либо в виде суммы передаваемого сигнала и помехи, и тогда помеху называют аддитивной, либо просто шумом, либо в виде произведения передаваемого сигнала и помехи, и тогда такую помеху называют мультипликативной. Эта помеха приводит к значительным изменениям интенсивности сигнала на входе приемника и объясняет такие явления как замирания.

Наличие помех затрудняет прием сигналов при большой интенсивности помех, распознавание сигнала может стать практически невозможным. Способность системы противостоять мешающему воздействию помехи носит название помехоустойчивости.

Внешние естественные активные помехи представляют собой шумы, возникающие в результате радиоизлучения земной поверхности и космических объектов, работы других радиоэлектронных средств. Комплекс мероприятий, направленных на уменьшение влияния взаимных помех РЭС, называется электомагнитной совместимостью. Этот комплекс включает в себя как технические меры совершенствования радиоаппаратуры, выбор формы сигнала и способа его обработки, так и организационные меры: регламентация частоты, разнесение РЭС в пространстве, нормирование уровня внеполосных и побочных излучений и др.

11. Дискретизация непрерывных сигналов. Теорема Котельникова (отсчётов). Понятие частоты Найквиста. Понятие интервала дискретизации.