
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Временной и спектральный методы анализа передачи сигналов через линейные цепи
Пусть на вход линейной стационарной цепи подан сигнал Sвх(t). На основании определений дельта-функции и ее фильтрующего свойства входной сигнал может быть представлен в виде интеграла
Sвх(t)= 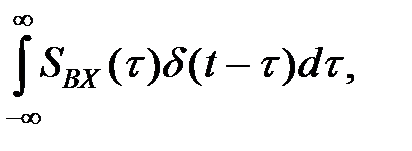 (10)
(10)
поскольку он является предельным выражением суммы, которой входной сигнал представляется как бесконечная последовательность дельта- импульсов, смешенных друг относительно друга на время t. Амплитуда импульсов равна значению сигнала в те же моменты времени t (см. рис.)
| S(t) |
| t1 t2 |
| t |
| t |
Если установить реакцию цепи на отдельный дельта-импульс, то в силу линейности и стационарности цепи можно просуммировать отдельные реакции и получить выходной отклик на любое входное воздействие. Поэтому вводят импульсную характеристику цепи h(t), являющуюся выходным откликом на входной дельта-импульс. Таким образом, выходная реакция Sвых(t) на произвольное входное воздействие может быть представлена интегралом
Sвых(t)= 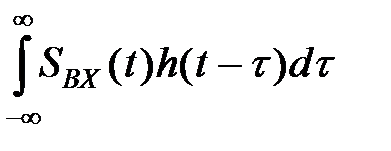 (11)
(11)
Из (11) следует, что сигнал на выходе цепи Sвых(t) в момент t получается суммированием мгновенных значений входного сигнала Sвх(t) с весом h(t-t) за все предыдущее время с начала сигнала. Импульсная характеристика и метод интеграла наложения являются основными понятиями при исследовании прохождения сигналов через линейные цепи методом интеграла наложения.
Соотношение (11) может быть записано также в виде
Sвых(t)= 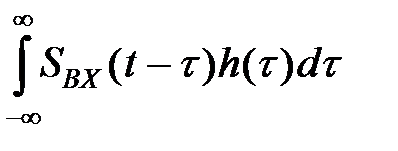 (12)
(12)
Представим входной сигнал в виде интеграла Фурье
Sвх(t)= 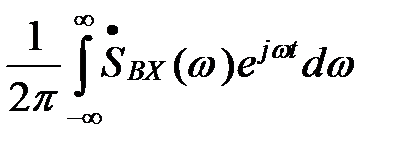
Если сделать подстановку t=t ’ -t (а потом отбросить штрих у t), то можно записать, что
Sвх(t-t)= 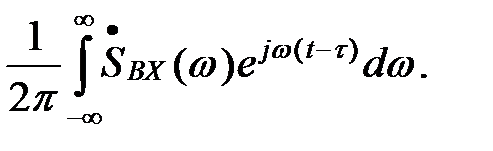
Подставив это выражение в (12) и изменив порядок интегрирования, получим
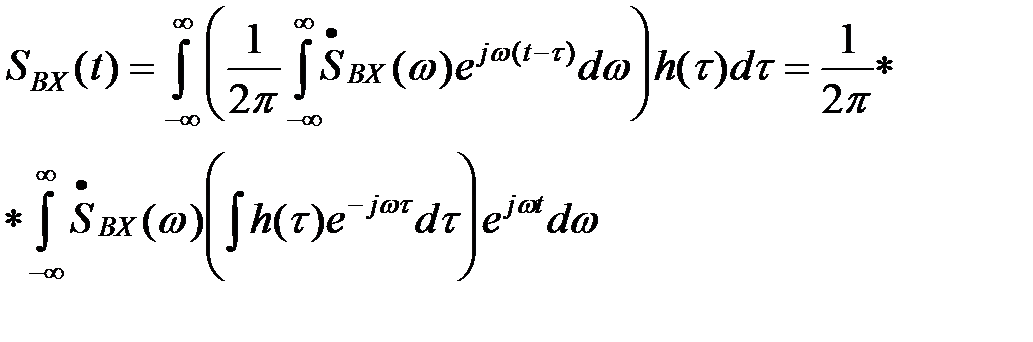 (13)
(13)
Внутренний интеграл является комплексной функцией частоты. Обозначим его как
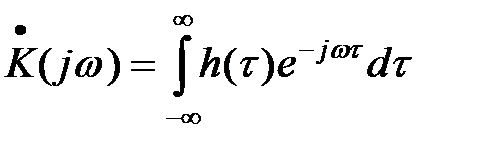 ®
® 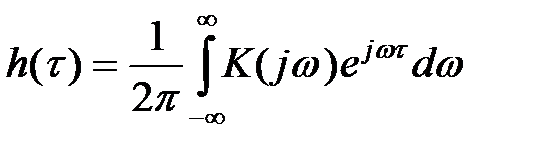 (14)
(14)
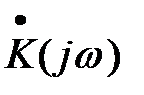 является прямым преобразованием Фурье для импульсной функции цепи. Его функции называют частотным коэффициентом передачи цепи (или комплексной частотной характеристикой).
является прямым преобразованием Фурье для импульсной функции цепи. Его функции называют частотным коэффициентом передачи цепи (или комплексной частотной характеристикой).
Частотному коэффициенту передачи можно дать и другие эквивалентные толкования. Одно из них получается в результате подстановки (14) в (13):
Sвых(t)= 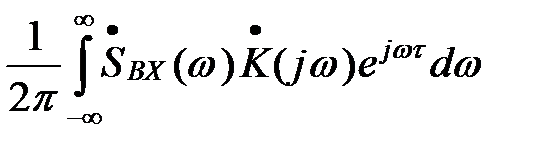 (15)
(15)
Как видно, полученное выражение совпадает с обратным преобразованием Фурье для спектра выходного сигнала, поскольку
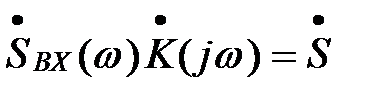 ВЫХ(w), (16)
ВЫХ(w), (16)
или, другими словами, частотный коэффициент передачи есть множитель пропорциональности между спектральными плотностями входного и выходного сигналов. Отсюда возникло название метода анализа прохождения сигналов через линейные цепи, основанного на использовании частотного коэффициента передачи, как спектрального метода.
Практически частотный коэффициент передачи удобнее вычислять пользуясь другим его определением. Для этого рассмотрим в качестве входного сигнала гармоническое колебание в комплексной форме: SВХ(t)= 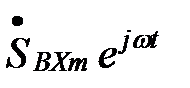 . Гармоническое колебание, сдвинутое во времени SBX(t-t)=
. Гармоническое колебание, сдвинутое во времени SBX(t-t)= 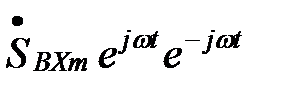 . Подставив это выражение в (12), выносят из под интеграла функции, не зависящие от переменной интегрирования и перегруппировав члены, получим:
. Подставив это выражение в (12), выносят из под интеграла функции, не зависящие от переменной интегрирования и перегруппировав члены, получим:
SВХ(t)= 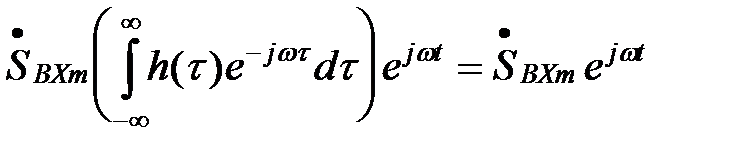 .
.
Здесь интеграл есть частотный коэффициент передачи. Таким образом, 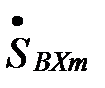
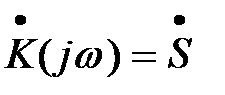 ВЫХm , откуда
ВЫХm , откуда
 (17)
(17)
и, следовательно, коэффициент передачи равен отношению комплексных амплитуд гармонических колебаний на выходе и входе линейной цепи. Частотный коэффициент передачи обычно записывают в показательной форме
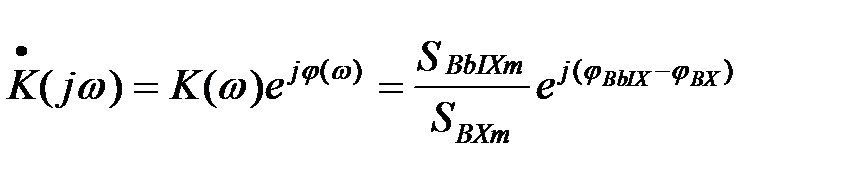 (18)
(18)
где K(w)=| 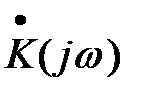 | - амплитудно-частотная характеристика цепи (АЧХ) j(w)=jвых-jвх - фазочастотная характеристика цепи (ФЧХ).
| - амплитудно-частотная характеристика цепи (АЧХ) j(w)=jвых-jвх - фазочастотная характеристика цепи (ФЧХ).
Из соотношения (12) следует еще один метод практического определения импульсной характеристики h(t):
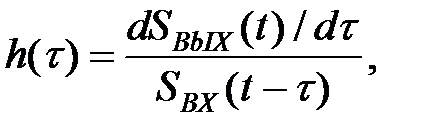 (19)
(19)
где t - время анализа, 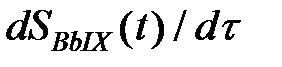 - скорость изменения выходного сигнала
- скорость изменения выходного сигнала 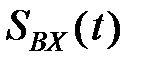 в течении времени анализа t,
в течении времени анализа t, 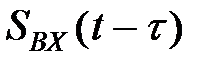 - значения входного сигнала в течении времени анализа t.
- значения входного сигнала в течении времени анализа t.
Таким образом, импульсная характеристика характеризует скорость изменения выходного сигнала за время анализа по отношению к мгновенным значениям входного сигнала в течении этого же интервала времени. Для ее определения достаточно знать форму входного и выходного сигналов за время действия пробного сигнала. Отсюда понятно и введение понятия пробного сигнала.
Сущность операторного метода заключается в том, что функции 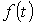 вещественной переменной t, которую называют оригиналом, ставится в соответствие функция
вещественной переменной t, которую называют оригиналом, ставится в соответствие функция  комплексной переменной
комплексной переменной 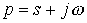 , которую называют изображением. В результате этого производные и интегралы от оригиналов заменяются алгебраическими функциями от соответствующих изображений (дифференцирование заменяется умножением на оператор р, а интегрирование – делением на него), что в свою очередь определяет переход от системы интегро-дифференциальных уравнений к системе алгебраических уравнений относительно изображений искомых переменных. При решении этих уравнений находятся изображения и далее путем обратного перехода – оригиналы. Важнейшим моментом при этом в практическом плане является необходимость определения только независимых начальных условий, что существенно облегчает расчет переходных процессов в цепях высокого порядка по сравнению с классическим методом.
, которую называют изображением. В результате этого производные и интегралы от оригиналов заменяются алгебраическими функциями от соответствующих изображений (дифференцирование заменяется умножением на оператор р, а интегрирование – делением на него), что в свою очередь определяет переход от системы интегро-дифференциальных уравнений к системе алгебраических уравнений относительно изображений искомых переменных. При решении этих уравнений находятся изображения и далее путем обратного перехода – оригиналы. Важнейшим моментом при этом в практическом плане является необходимость определения только независимых начальных условий, что существенно облегчает расчет переходных процессов в цепях высокого порядка по сравнению с классическим методом.
Изображение  заданной функции
заданной функции 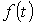 определяется в соответствии с прямым преобразованием Лапласа:
определяется в соответствии с прямым преобразованием Лапласа:
 . .
| (1) |
В сокращенной записи соответствие между изображением и оригиналом обозначается, как:
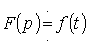
| или | 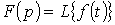 . .
|
Следует отметить, что если оригинал 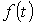 увеличивается с ростом t, то для сходимости интеграла (1) необходимо более быстрое убывание модуля
увеличивается с ростом t, то для сходимости интеграла (1) необходимо более быстрое убывание модуля 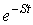 . Функции, с которыми встречаются на практике при расчете переходных процессов, этому условию удовлетворяют.
. Функции, с которыми встречаются на практике при расчете переходных процессов, этому условию удовлетворяют.
В качестве примера в табл. 1 приведены изображения некоторых характерных функций, часто встречающихся при анализе нестационарных режимов.
Таблица 1. Изображения типовых функций
Оригинал 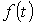
| А | 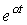
| 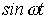
| 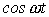
| 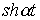
| 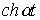
|
Изображение 
| 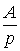
| 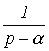
| 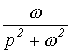
| 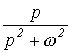
| 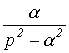
| 
|
15. Радиосигналы с амплитудной модуляцией. Математическая модель, спектральная характеристика, особенности применения. Радиосигналы с угловой модуляцией (частотной и фазовой). Математическая модель, спектральная характеристика, особенности применения.
АМПЛИТУДНАЯ МОДУЛЯЦИЯ
При амплитудной модуляции по закону управляющего сигнала и(t) изменяется амплитуда колебаний:
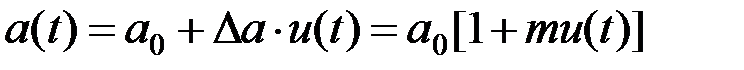 (2.3.2)
(2.3.2)
где 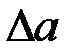 – максимальное абсолютное изменение амплитуды, а
– максимальное абсолютное изменение амплитуды, а 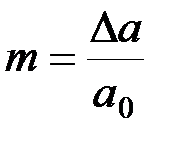 – относительное изменение амплитуды, называемое коэффициентом модуляции.
– относительное изменение амплитуды, называемое коэффициентом модуляции.
АМ колебание записывается в виде
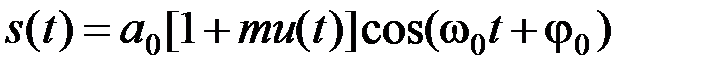 (2.3.3)
(2.3.3)
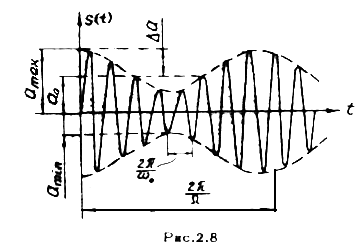
и для случая модуляции чистым тоном 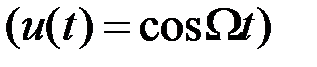 имеет вид, показанный на рис.2.8. Очевидно, чтобы не было искажений, коэффициент модуляции должен быть меньше единицы. Из графика для АМ колебаний видно, что
имеет вид, показанный на рис.2.8. Очевидно, чтобы не было искажений, коэффициент модуляции должен быть меньше единицы. Из графика для АМ колебаний видно, что
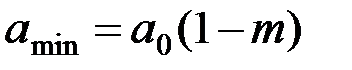
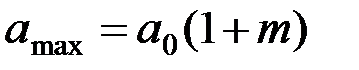
откуда имеем
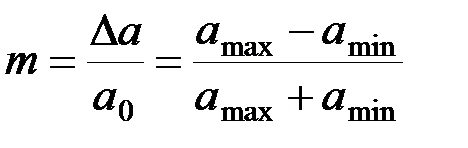 (2.3.4)
(2.3.4)
Определим спектр АМ колебаний при модуляции чистым тоном. Это можно сделать с помощью преобразования Фурье. Однако проще его подучить с помощью простых тригонометрических преобразований. Действительно, полагая в (2.3.3) и(t)= соsΩ t,
Получим
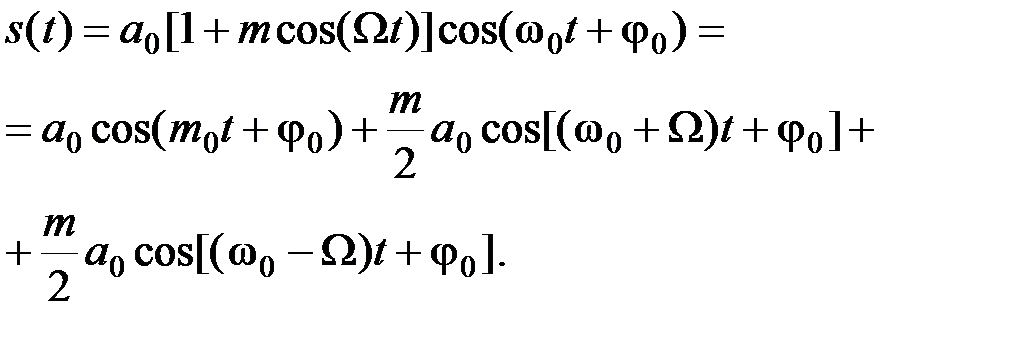 (2.3.5)
(2.3.5)
Замечаем, что АМ колебание имеет дискретный спектр и состоит из трех не кратных гармонических составляющих: колебания несущей частоты 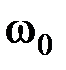 с амплитудой
с амплитудой 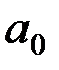 и двух колебаний с амплитудами
и двух колебаний с амплитудами 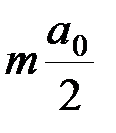 и частотами
и частотами 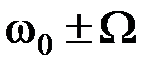 , которые называются боковыми частотами. Спектр АМ колебания показан на рис. 2.9. Ширина спектра АМ-сигнала равна
, которые называются боковыми частотами. Спектр АМ колебания показан на рис. 2.9. Ширина спектра АМ-сигнала равна 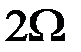 .
.
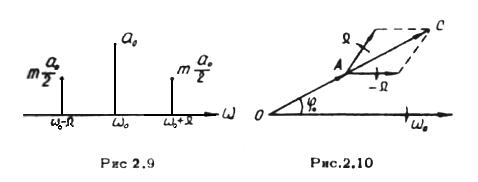
Как известно, гармонические колебания часто представляв в виде векторов. Аналогично можно построить векторную диаграмму для АМ колебания, которая показана на рис.2.10.
При построении диаграммы предполагалось, что плоскость чертежа вращается по часовой стрелке со скоростью 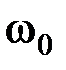 . Поэтому вектор несущего колебания ОА неподвижен относительно оси времени. Векторы боковых колебаний вращаются относительно вектора несущей со скоростью
. Поэтому вектор несущего колебания ОА неподвижен относительно оси времени. Векторы боковых колебаний вращаются относительно вектора несущей со скоростью 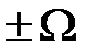 , т.е. в противоположные стороны. Результирующий вектор ОС в результате этого изменяется только по длине, но не по направлению.
, т.е. в противоположные стороны. Результирующий вектор ОС в результате этого изменяется только по длине, но не по направлению.
В более общем случае, когда модуляция осуществляется сложным периодическим сигналом, который можно разложить в ряд Фурье
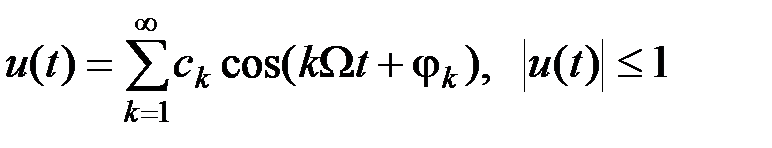 (2.3.6)
(2.3.6)
выражение для АМ - колебания можно представить в виде
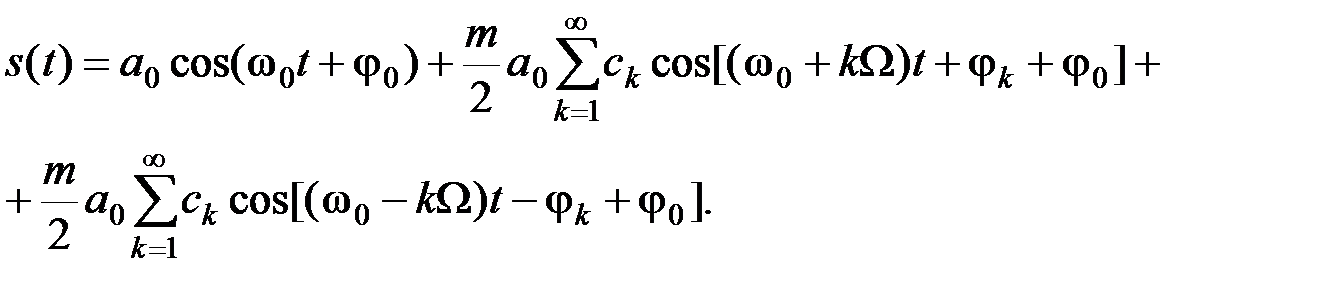 (2.3.7)
(2.3.7)
В этом случае АМ колебание состоит из колебания несущей частоты 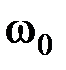 и двух боковых полос с суммарными
и двух боковых полос с суммарными  и разностными
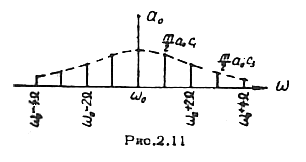
и разностными 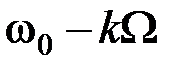 частотами. Спектр такого колебания показан на рис.2.11.
частотами. Спектр такого колебания показан на рис.2.11.
Если спектр модулирующего колебания ограничен сверху частотой 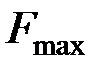 , то ширина спектра модулированного колебания равна
, то ширина спектра модулированного колебания равна 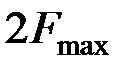
Заметим, что огибающая амплитуд боковых частот с точностью до постоянного множителя 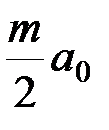 , совпадает с огибающей спектра амплитуд модулирующей функции. Это позволяет легко построить амплитудный спектр АМ колебания, если известен спектр модулирующей функции. Для построения необходимо сместить спектр модулирующей функции по оси частот на величину
, совпадает с огибающей спектра амплитуд модулирующей функции. Это позволяет легко построить амплитудный спектр АМ колебания, если известен спектр модулирующей функции. Для построения необходимо сместить спектр модулирующей функции по оси частот на величину  , получая при этом верхнюю боковую полосу; нижняя боковая полоса будет являться зеркальным отображением верхней относительно частоты
, получая при этом верхнюю боковую полосу; нижняя боковая полоса будет являться зеркальным отображением верхней относительно частоты  .
.
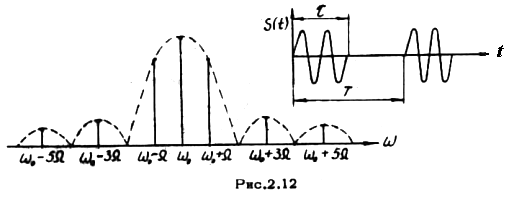
Проиллюстрируем сказанное на примере амплитудной манипуляции (рис.2.12). В случае манипуляции модулирующая функция представляет собой периодическую последовательность прямоугольных импульсов и согласно (2.2.12) при 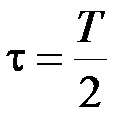 ,
, 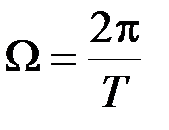 разлагается в следующий ряд Фурье
разлагается в следующий ряд Фурье
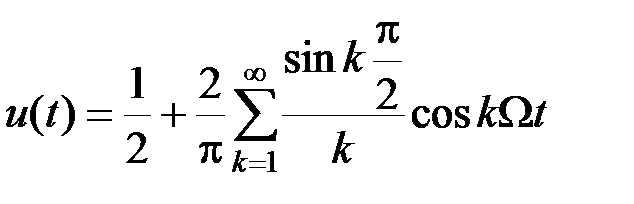 (2.3.8)
(2.3.8)
Амплитудно-манипулированное колебание при этом записывается в виде
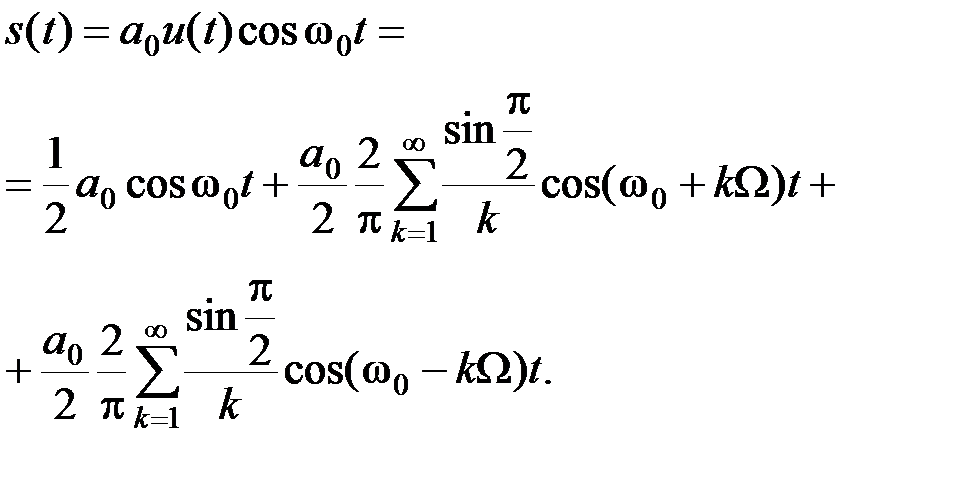 (2.3.9)
(2.3.9)
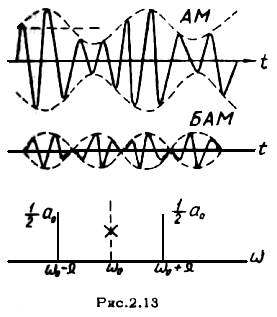
Амплитудный спектр манипулированного колебания показан на рис.2.13.
Амплитудно-модулированные колебания являются типичным примером почти периодических сигналов, для которых гармонические составляющие имеют некратные частоты.
Рассмотрим энергетические соотношения при АМ. В соответствии с изменением амплитуды колебания изменяется и средняя за период высокой частоты мощность модулированного колебания.
Мощность сигнала в отсутствии модуляции (мощность несущего колебания) определяется первым членом выражения (2.3.5) и равна
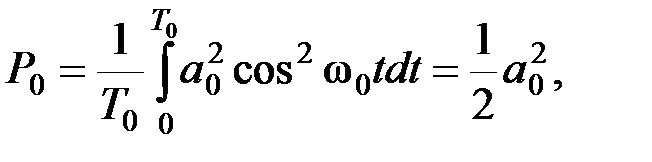 (2.3.10)
(2.3.10)
где 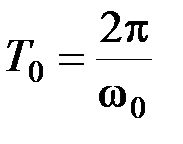 – период высокочастотного колебания.
– период высокочастотного колебания.
В режиме модуляции мощность непрерывно изменяется. Ее максимальное и минимальное значения соответственно определяется выражениями
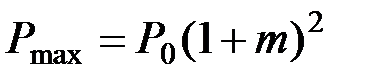 ,
, 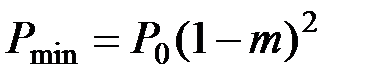 (2.3.11)
(2.3.11)
Мощность двух боковых частот (при модуляции чистым тоном) при 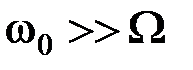 будет равна
будет равна
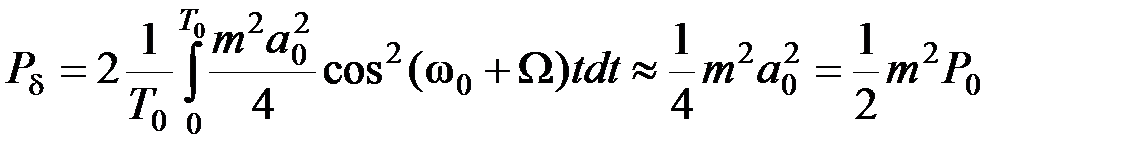 (2.3.12)
(2.3.12)
Средняя за период модуляции мощность будет равна
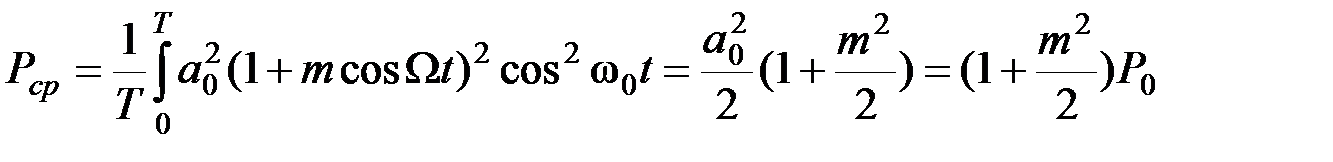 (2.3.13)
(2.3.13)
где 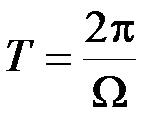 – период модулирующего колебания. Из последних выражений при m = 1 получим
– период модулирующего колебания. Из последних выражений при m = 1 получим
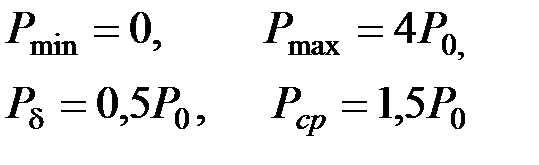 (2.3.14)
(2.3.14)
Таким образом, при стопроцентной модуляции 2/3 всей мощности тратится на передачу несущего колебания и 1/З - на передачу боковых частот. Обусловленное модуляцией приращение мощности, которое в основном и определяет условия выделения сообщения при приеме, в этом случае не превышает половины мощности несущего колебания. Кроме того, большая величина пиковой мощности по сравнению со средней требует линейного режима работы тракта приема-передачи в широком динамическом диапазоне (в передатчике лампы должны выбираться по максимальной мощности). Сказанное позволяет заключить, что амплитудная модуляция с энергетической точки зрения имеет существенные недостатки.
Указанные недостатки амплитудной модуляции можно в значительной мере устранить, если использовать передачу с подавленной несущей. Подавление несущей осуществляется ори использовании балансной амплитудной модуляции (БАМ). Этот вид модуляции называют еще двухполосной модуляцией (ДМ) При балансной модуляции сигнал записывается в виде
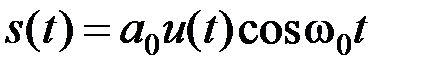 (2.3.15)
(2.3.15)
откуда при модуляции чистым тоном получим
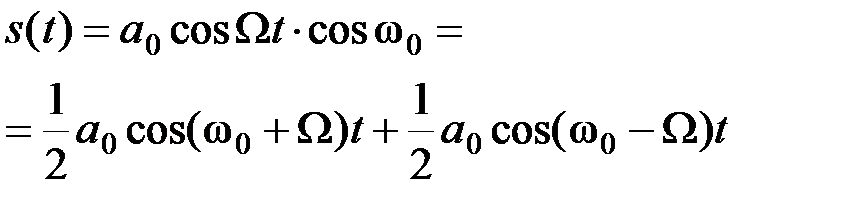 (2.3.16)
(2.3.16)
т.е. только две боковые частоты без несущей.
При балансной модуляции аналогично (2.3.10) - (2.3.13) находим
 (2.3.17)
(2.3.17)
Следовательно, энергетические показатели в этом случае значительно лучше, чем при обычной АМ.
На рис.2.13 показан спектр сигнала при балансной модуляции и временные диаграммы при обычной и балансной модуляции и временная диаграмма в последнем случае получается путем вычитания из обычного АМ колебания составляющей 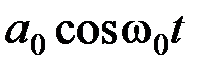 . Нетрудно видеть, что огибающая при балансной модуляции имеет удвоенную частоту, а фаза высокочастотного заполнения меняется скачком на 180 при каждом переходе огибающей через нулевое значение. Весьма показательным примером этого мох служить амплитудно-манипулированное колебание с подавленной несущей (рис.2.14). Такое колебание по сути дела будет являться фазоманипулированным колебанием, которое будет рассмотрено подробнее несколько ниже. Однако уже сейчас можно отметить, что фазоманипулированное колебание будет иметь амплитудный спектр АМ колебания с подваленной несущей.
. Нетрудно видеть, что огибающая при балансной модуляции имеет удвоенную частоту, а фаза высокочастотного заполнения меняется скачком на 180 при каждом переходе огибающей через нулевое значение. Весьма показательным примером этого мох служить амплитудно-манипулированное колебание с подавленной несущей (рис.2.14). Такое колебание по сути дела будет являться фазоманипулированным колебанием, которое будет рассмотрено подробнее несколько ниже. Однако уже сейчас можно отметить, что фазоманипулированное колебание будет иметь амплитудный спектр АМ колебания с подваленной несущей.
Еще одной разновидностью АМ является однополосная модуляция (ОМ или ОБП), при которой передается только одна боковая полоса частот. При модуляции чистым тоном в этом случае из (2.3.16) имеем
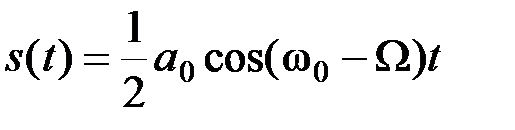
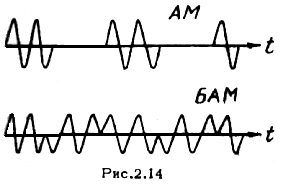
Использование БАМ и ОМ позволяет сократить бесполезный расход энергии на составляющую несущей частоты, а при ОМ - сократить дополнительно вдвое ширину спектра передаваемого сигнала. Однако для демодуляции сигнала на приемной стороне несущая необходима. Необходимость восстановления несущей требует некоторого усложнения аппаратуры.
ЧАСТОТНАЯ МОДУЛЯЦИЯ
При частотной модуляция по закону модулирующего колебания и(t) изменяется частота высокочастотного несущего колебания.
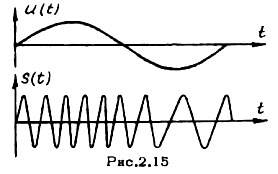
На рис.2.15 показаны графики модулирующего и модулированного сигналов в случае модуляции чистым тоном.
Получим выражение для ЧМ - колебания. По определению
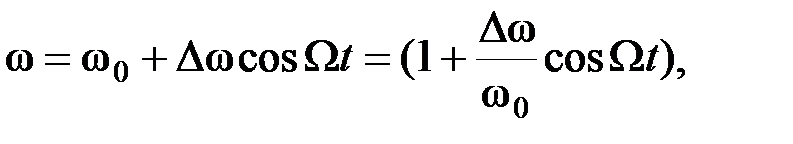 (2.3.17)
(2.3.17)
где 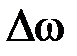 - максимальное отклонение частоты, называемое девиацией частоты, а
- максимальное отклонение частоты, называемое девиацией частоты, а 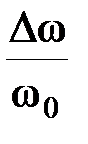 - относительное изменение частоты.
- относительное изменение частоты.
По своему определению мгновенная круговая частота является производной по времени от аргумента тригонометрической функции 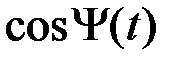 , представляющей колебание, т. е.
, представляющей колебание, т. е. 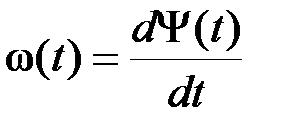 (2.3.18)
(2.3.18)
Из последнего выражения получим
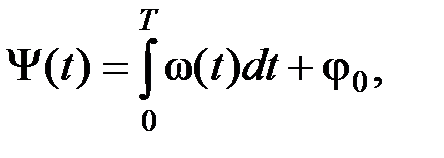 (2.3.19)
(2.3.19)
т.е. фаза колебания определяется интегралом от круговой частоты. Поэтому для ЧМ - колебания при модуляции чистым тоном можно записать
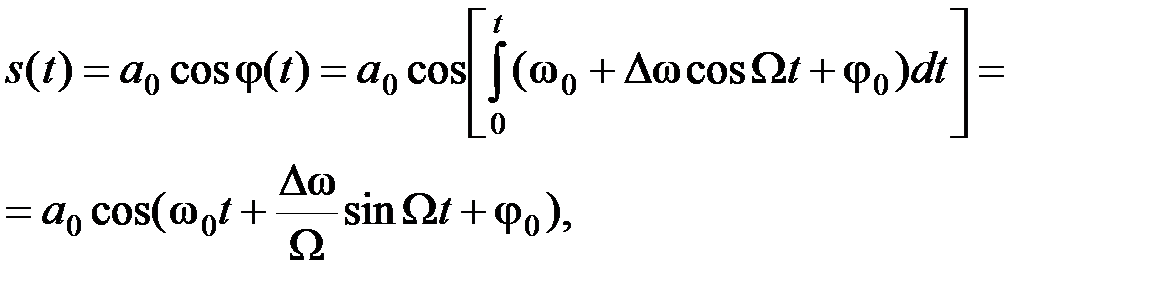 (2.3.20)
(2.3.20)
Замечаем, что изменение частоты по закону 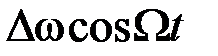 приводит к изменению фазы по закону
приводит к изменению фазы по закону 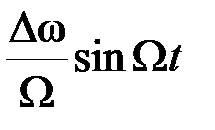 . Величина
. Величина 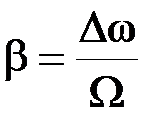 называется индексом частотной модуляции и имеет смысл максимальной величины (амплитуды) изменения фазы при частотной модуляции.
называется индексом частотной модуляции и имеет смысл максимальной величины (амплитуды) изменения фазы при частотной модуляции.
Заменяя косинус суммы двух углов по известным формулам тригонометрии, вместо (2.3.20) при 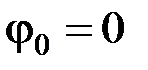 получим
получим
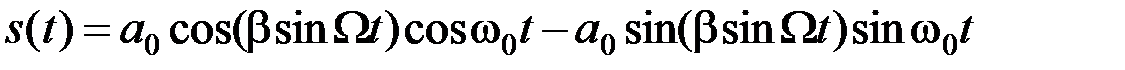 (2.3.21)
(2.3.21)
Определим теперь спектр частотно-модулированного сигнала. Начнем со случая малого индекса модуляции, когда 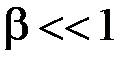 . В этом случае
. В этом случае
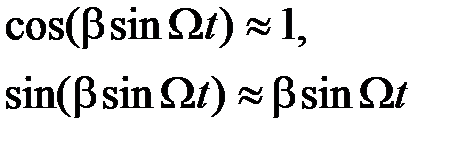 (2.3.22)
(2.3.22)
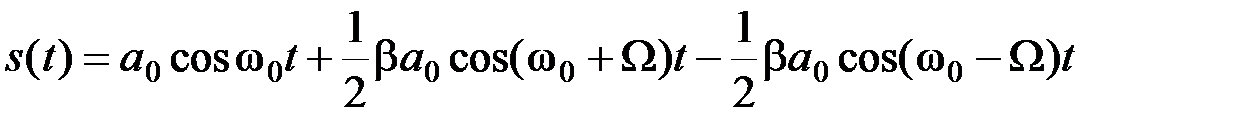 (2.3.23)
(2.3.23)
Замечаем, что при малом индексе модуляции спектр ЧМ колебания отличается от спектра АМ - колебания только сдвигом фазы нижней боковой частоты на 180. Это иллюстрируется рис.2.16, на котором показана векторная диаграмма для ЧМ колебания (сравни с рис.2.10).
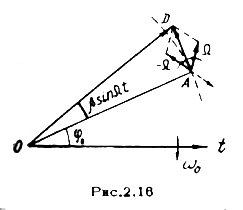
На диаграмме результирующий вектор ОД изменяется как по фазе, так и амплитуде, однако при  амплитудные изменения настолько малы, что ими можно пренебречь. При произвольных значениях β с учетом всех частотных составляющих спектра результирующий вектор будет изменяться только по фазе.
амплитудные изменения настолько малы, что ими можно пренебречь. При произвольных значениях β с учетом всех частотных составляющих спектра результирующий вектор будет изменяться только по фазе.
Определим теперь спектр ЧМ колебания при произвольном Рис.2.16 индексе модуляции. Для этого периодические функции 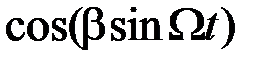 и
и 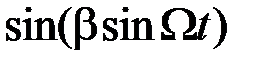 разложим в ряды Фурье, коэффициенты которых, как доказывается в теории бесселевых функций, являются функциями Бесселя первого рода:
разложим в ряды Фурье, коэффициенты которых, как доказывается в теории бесселевых функций, являются функциями Бесселя первого рода:
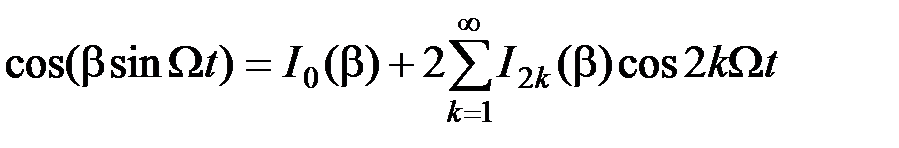
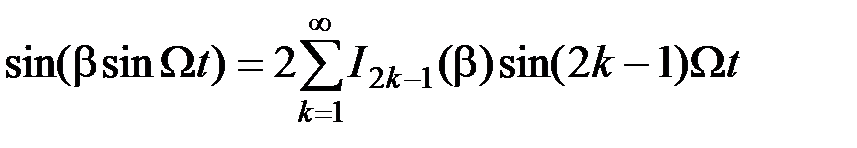 (2.3.24)
(2.3.24)
Подставляя последние выражения в (2.3.21) и производя тригонометрические преобразования, окончательно получим
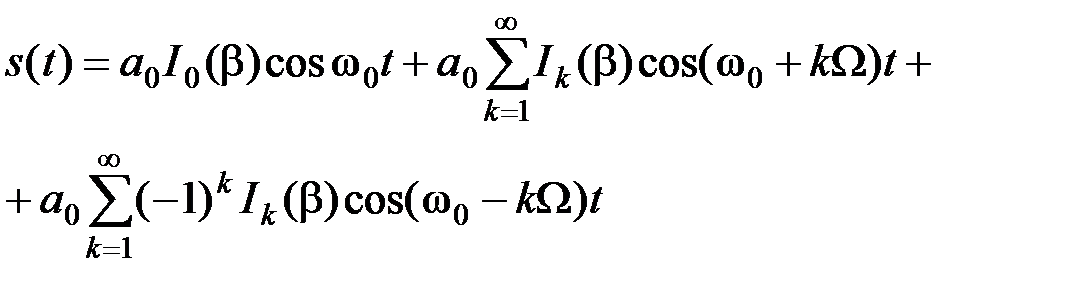 (2.3.25)
(2.3.25)
Таким образом, ЧМ колебание имеет дискретный спектр и состоит из несущей и бесконечного числа боковых частот 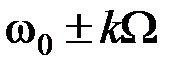 с амплитудами
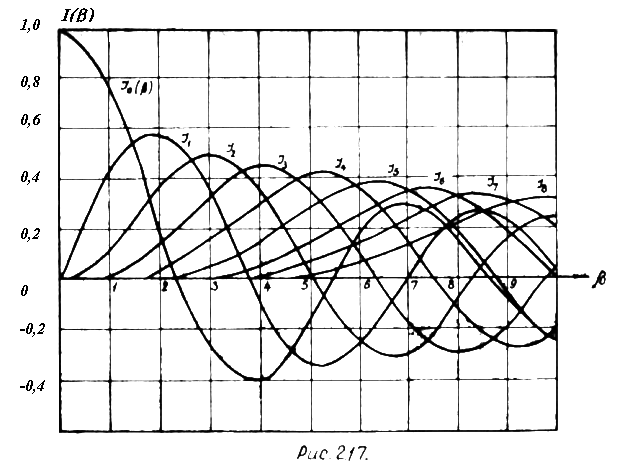
с амплитудами 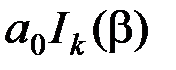 . Однако практически ширина спектра при частотной модуляции ограничена. Это можно заметить из рис.2.17, на котором приведены графики функций
. Однако практически ширина спектра при частотной модуляции ограничена. Это можно заметить из рис.2.17, на котором приведены графики функций 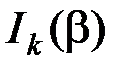 . При
. При 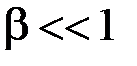 и
и 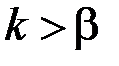 функции
функции 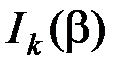 убывают столь быстро, что ими можно пренебречь, т.е. считать, что
убывают столь быстро, что ими можно пренебречь, т.е. считать, что 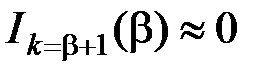 . Поэтому ширина спектра при широкополосной ЧМ (
. Поэтому ширина спектра при широкополосной ЧМ (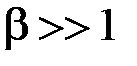 ) будет равна
) будет равна
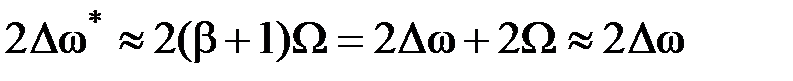 (2.3.26)
(2.3.26)
т.е. приближенно равна удвоенной девиации частоты.
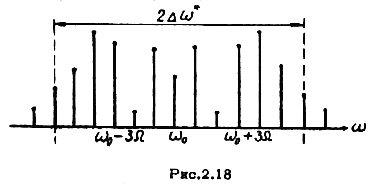
На рис.2.18 в качестве примера показан график модуля спектра ЧМ колебания при 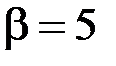 .
.
Таким образом, ширина спектра при широкополосной ЧМ в 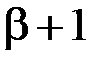 раз шире, чем при обычной АМ. Преимуществом частотной модуляции является постоянство мощности, так как амплитуда сигнала в процессе модуляции не изменяется.
раз шире, чем при обычной АМ. Преимуществом частотной модуляции является постоянство мощности, так как амплитуда сигнала в процессе модуляции не изменяется.
Отметим теперь, что при частотной модуляции девиация частоты 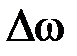 определяется амплитудой модулирующего сигнала и(t). При уменьшении амплитуды модулирующего сигнала уменьшается индекс модуляции
определяется амплитудой модулирующего сигнала и(t). При уменьшении амплитуды модулирующего сигнала уменьшается индекс модуляции 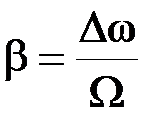 и действительная ширина спектра
и действительная ширина спектра 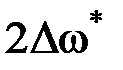 . При постоянной амплитуде и
. При постоянной амплитуде и 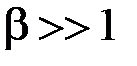 изменение частоты модулирующего сигнала Ω изменяет индекс модуляции, число линий и интервал между линиями в спектре ЧМ колебания, однако ширина спектра
изменение частоты модулирующего сигнала Ω изменяет индекс модуляции, число линий и интервал между линиями в спектре ЧМ колебания, однако ширина спектра 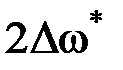 практически остается постоянной.
практически остается постоянной.
Выше рассматривался случай модуляции чистым тоном. По модуляции сложным сигналом спектр ЧМ колебания будет гораздо богаче, а ширина спектра при 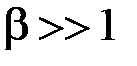 будет равна
будет равна
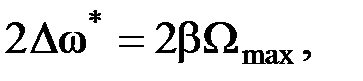
где Ω тах - максимальная круговая частота в спектре модулирующего сигнала.
В качестве примера рассмотрим случай частотной манипуляции (рис.2.19), когда модулирующая функция представляет собой периодическую последовательность прямоугольных импульсов с частотой Ω. В этом случае частота заполнения принимает два дискретных значения 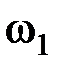 и
и 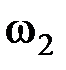 .
.
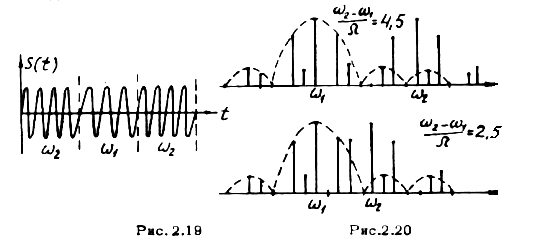
Частотно-манипулированное колебание можно представит в виде суммы двух амплитудно-манипулированных колебаний с несущими частотами 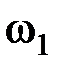 и
и 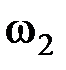 , поэтому, согласно (2.1.29) его спектр будет равен сумме спектров последних. На рис.2.20 показаны амплитудные спектры частотно-манипулированных сигналов для различных соотношений между
, поэтому, согласно (2.1.29) его спектр будет равен сумме спектров последних. На рис.2.20 показаны амплитудные спектры частотно-манипулированных сигналов для различных соотношений между 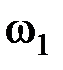 и
и 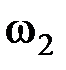 .
.
Заметим, что эти две частоты при передаче дискретных сообщений условно называют частотами ''нажатия'' и "отжатия".
ФАЗОВАЯ МОДУЛЯЦИЯ
При фазовой модуляции в соответствии с модулирующим сигналом изменяется фаза высокочастотного колебания (2.3.1)
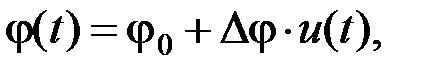 (2.3.27)
(2.3.27)
где 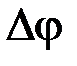 - индекс фазовой модуляции. При модуляции чистым тоном имеем
- индекс фазовой модуляции. При модуляции чистым тоном имеем
 (2.3.28)
(2.3.28)
Сравнивая (2.3.28) и (2.3.20), можно заметить, что выражения для ФМ и ЧМ по форме записи одинаковы. Однако при ФМ в аргумент тригонометрической функции входит модулирующая функция u(t), а при ЧМ - интеграл от нее. При модуляции чистым тоном и одинаковых индексах модуляции 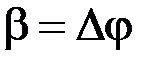 разницы в форме и спектрах этих колебаний нет. Различие между ними заключается в различном определении индексов модуляции. При фазовой модуляции индекс модуляции
разницы в форме и спектрах этих колебаний нет. Различие между ними заключается в различном определении индексов модуляции. При фазовой модуляции индекс модуляции 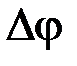 пропорционален амплитуде модулирующего напряжения и не зависит от его частоты. При ЧМ величина девиации
пропорционален амплитуде модулирующего напряжения и не зависит от его частоты. При ЧМ величина девиации 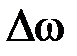 пропорциональна амплитуде модулирующего напряжения, а индекс модуляции
пропорциональна амплитуде модулирующего напряжения, а индекс модуляции 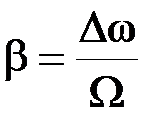 зависит от частоты модуляции. Появление множителя
зависит от частоты модуляции. Появление множителя 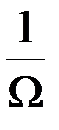 означает необходимость введения соответствующих корректирующих цепей: если для приема ФМ сигналов используется приемник ЧМ сигналов, то в последнем необходимо добавить интегрирующее звено.
означает необходимость введения соответствующих корректирующих цепей: если для приема ФМ сигналов используется приемник ЧМ сигналов, то в последнем необходимо добавить интегрирующее звено.
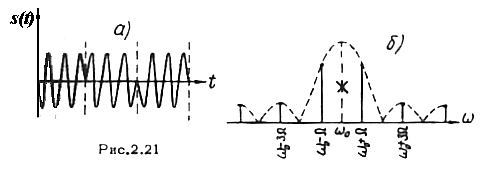
Существенное различие между ФМ и ЧМ обнаруживается при сложных модулирующих сигналах, т.е. когда модулирующая функция обладает богатым спектром. В качестве примера можно рассмотреть случай фазовой манипуляции (рис.2.21 а). Как отмечалось выше, такой сигнал можно рассматривать как АМ колебание с подавленной несущей, спектр которого показан на рис. 2.21 б. (ср. с рис.2.20).
Этот же результат можно получить, если рассматривать ФМ колебание как сумму двух АМ колебаний, одно из которых сдвинуто по фазе на 180 и по времени на величину 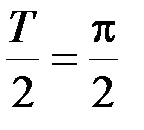 . Поэтому, согласно (2.1.29), можно написать
. Поэтому, согласно (2.1.29), можно написать
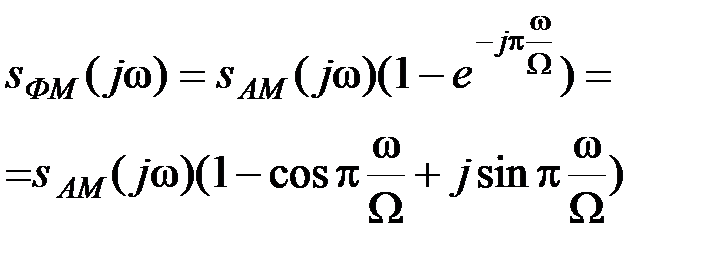 (2.3.29)
(2.3.29)
где 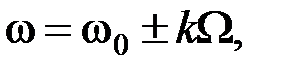 к =0;1;2;...
к =0;1;2;...
При целом числе периодов высокочастотного колебания на интервале 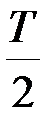
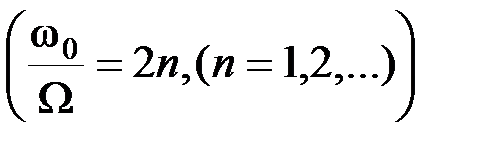 получим
получим
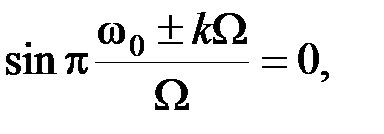
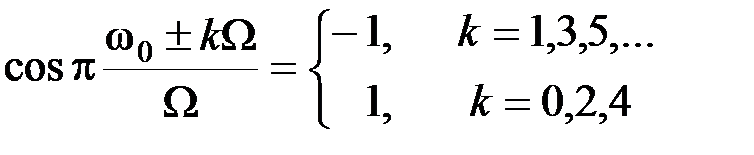
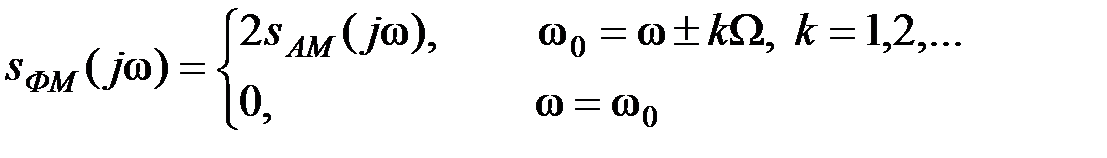
Таким образом, приходим к результату, показанному на рис. 2.21 б.
В заключение этого раздела заметим, что фазовую и частотную модуляцию часто называют угловой модуляцией. Однако при объединении их под одним названием необходимо помнить, что между ними в общем случае имеются существенно различия как в форме колебаний, так и их спектрах.
17. Корреляционный анализ сигналов. Понятие автокорреляционной и взаимной корреляционной функций.
Date: 2015-07-27; view: 1490; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |