Определение 1.19. Рангом совместной системы линейных алгебраических уравнений называется ранг ее матрицы

Предположим, что система (1.4) совместная и ранг ее равняется.

Отделим в матрицы системы (1.4) некоторый базисный минор. Без ограничения общности соображений можно предположить, что он состоит из первых строк и первых столбцов матрицы, то есть:

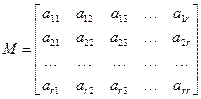. (1.6)

В расширенной матрице 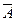базисными строками, которые отвечают этому минору, будут первые строк. В соответствии с теоремой о базисном миноре всякая строка матрицы 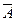есть линейной комбинацией ее базисных строк, то есть

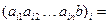
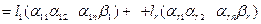(1.7)

Помножим первое уравнение системы на 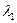, второе на 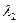, …, на 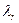и сложим их между собою. Причем отделим слагаемые, которые содержат , , …, .

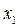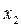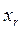При этом получим:

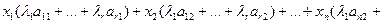
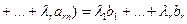
В соответствии с (1.7) это эквивалентно

.

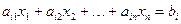Таким образом, любое уравнение системы (1.4) является линейной комбинацией первых базисных уравнений. То есть любое уравнение есть следствием базисных уравнений. Таким образом, система, которая складывается только из базисных уравнений, эквивалентная исходной системе (1.4). Эта система имеет вид

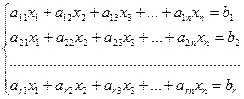(1.8)

Итак, вместо системы (1.5) можно решать систему (1.8), которая состоит только из линейно независимых (базисных) уравнений.

Сравним ранг СЛАУ 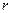с количеством неизвестных. Очевидно, что возможно только два варианта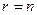: или , или 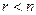. Рассмотрим их.

Вариант, когда 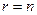. Итак, если 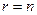, система (1.4) удовлетворяет условиям теоремы Крамера с 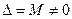и будет иметь единственное решение.

Вариант, когда 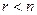. В системе (1.8)предоставим неизвестным 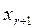, , 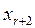…, 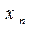произвольные числовые значения , , 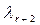…, 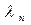и перенесем их в правую часть. В таком случае система (1.8) будет иметь вид:

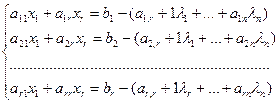(1.9)

Систему (1.9) можно рассматривать как систему уравнений с неизвестными. Определитель системы .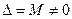

Таким образом, для каждого конкретного набора значений 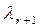, , 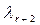…, 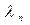система имеет единственное решение. Тем не менее разных наборов значений 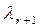, , 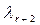…, 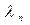может быть неисчислимое множество. Каждому такому набору отвечает один-единственный набор значений 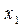, , 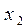…, 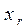. Итак, тогда система уравнений будет иметь бесчисленное множество решений.

Заметим, что при этом переменные 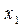, , 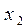…, 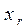называют базисными переменными, а переменные,, …, называют свободными переменными.

Приведенные соображения доказывают такие утверждения.

Date: 2015-07-10; view: 343; Нарушение авторских прав