
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

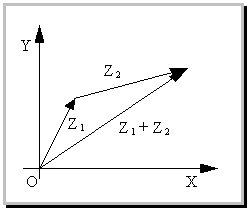
Геометрическое изображение суммы комплексных чисел
|
|
|
Согласно определению сложения двух комплексных чисел, действительная часть суммы равна сумме действительных частей слагаемых, мнимая часть суммы равна сумме мнимых частей слагаемых. Точно также определяются координаты суммы векторов:
Сумма двух векторов с координатами (A1;B1) и (A2;B2) есть вектор с координатами (A1+A2;B1+B2). Поэтому, чтобы найти вектор, соответствующий сумме комплексных чисел Z1 и Z2 нужно сложить векторы, соответствующие комплексным числам Z1 и Z2.
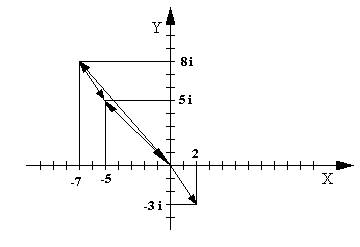
Пример: Найти сумму и произведение комплексных чисел Z1=2 – 3× i и
1 Способ:
Z2= –7 + 8 ×i.
Z1 + Z2 = 2 – 7 + (–3 + 8) ×i = – 5 + 5 ×i
Z1×Z2 = (2 – 3 ×i)×(–7 + 8 ×i) = –14 + 16 ×i + 21 ×i + 24 = 10 + 37 ×i
|
2 Способ:
ВЫЧИТАНИЕ И ДЕЛЕНИЕ КОМПЛЕКСНЫХ ЧИСЕЛ
Вычитание комплексных чисел – это операция, обратная сложению: для любых комплексных чиселZ1 и Z2 существует, и притом только одно, число Z, такое, что:
Z + Z2=Z1
Если к обеим частям равенства прибавить (–Z2) противоположное числу Z2:
Z+Z2+(–Z2)=Z1+(–Z2), откуда
Z = Z1 – Z2
Число Z=Z1+Z2 называют разностью чисел Z1 и Z2.
Деление вводится как операция, обратная умножению:
Z×Z2=Z1
Разделив обе части на Z2 получим:
Z= 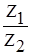
Из этого уравнения видно, что Z2 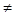 0
0
|
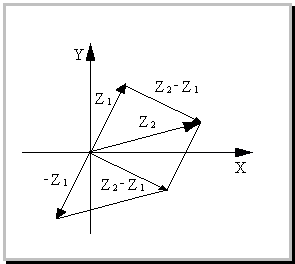
Геометрическое изображение разности комплексных чисел
Разности Z2 – Z1 комплексных чисел Z1 и Z2, соответствует разность векторов, соответствующих числам Z1 и Z2. Модуль  разности двух комплексных чиселZ2 и Z1 по определению модуля есть длина вектора Z2 – Z1. Построим этот вектор, как сумму векторов Z2 и (–Z1). Таким образом, модуль разности двух комплексных чисел есть расстояние между точками комплексной плоскости, которые соответствуют этим числам.
разности двух комплексных чиселZ2 и Z1 по определению модуля есть длина вектора Z2 – Z1. Построим этот вектор, как сумму векторов Z2 и (–Z1). Таким образом, модуль разности двух комплексных чисел есть расстояние между точками комплексной плоскости, которые соответствуют этим числам.
Это важное геометрическое истолкование модуля разности двух комплексных чисел позволяет с успехом использовать простые геометрические факты.
Пример: Даны комплексные числа Z1= 4 + 5 · i и Z2= 3 + 4 · i. Найти разность Z2 – Z1 и частное 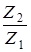
Z2 – Z1 = (3 + 4· i) – (4 + 5· i) = –1 – i
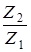 =
= 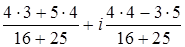 =
= 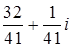
КВАДРАТНОЕ УРАВНЕНИЕ С КОМПЛЕКСНЫМ НЕИЗВЕСТНЫМ
Рассмотрим уравнение Z2 = a, где a – заданное действительное число, Z – неизвестное.
Это уравнение:
имеет один корень, если a = 0.
имеет два действительных корня Z1,2 = 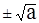 , если a > 0.
, если a > 0.
не имеет действительных корней, если a < 0. Но имеет два комплексных корня.
Запишем число a в виде a = (– 1)×(– a) = i 2×  = i 2×(
= i 2×(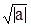 )2. Тогда уравнение Z2 = a запишется в виде:Z2 – i 2×(
)2. Тогда уравнение Z2 = a запишется в виде:Z2 – i 2×(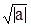 )2 = 0
)2 = 0
т.е. (Z – i × 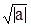 )(Z + i ×
)(Z + i × 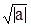 ) = 0
) = 0
Следовательно, уравнение имеет два корня: Z1,2 = 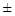 i ×
i × 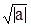
Введенное понятие корня из отрицательного числа позволяет записать корни любого квадратного уравнения с действительными коэффициентами
a×Z2 + b×Z + c = 0
По общей формуле Z1,2= 
Итак, при любых действительных a(a  0), b, c корни уравнения можно находить по формуле 10. При это если дискриминант, т.е. подкоренное выражение в формуле 10
0), b, c корни уравнения можно находить по формуле 10. При это если дискриминант, т.е. подкоренное выражение в формуле 10
D = b2 – 4×a×c
положителен, то уравнение a×Z2 + b×Z + c = 0 два действительных различных корня. Если D = 0, то уравнение a×Z2 + b×Z + c = 0 имеет один корень. Если D < 0, то уравнение a×Z2 + b×Z + c = 0 имеет два различных комплексных корня.
Комплексные корни квадратного уравнения обладают такими же свойствами, как и известные нам свойства действительных корней.
Сформулируем основные из них:
Пусть Z1,Z2 – корни квадратного уравнения a×Z2 + b×Z + c = 0, a  0. Тогда справедливы свойства:
0. Тогда справедливы свойства:
Теорема Виета: Z1 + Z2 = – 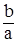
Z1×Z2 = 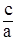
При всех комплексных Z справедлива формула
a×Z2 + b×Z + c = a×(Z – Z1)×(Z – Z2)
Пример 1:
Z2 – 6·Z + 10 = 0
Д = b2 – 4·a·c
Д = 62 – 4·10 = – 4
– 4 = i 2 ·4
Z1,2 = 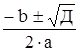
Z1,2 = 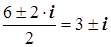
Ответ: Z1 = Z2 = 3 + i
Пример 2:
3·Z2 +2·Z + 1 = 0
Д = b2 – 4·a·c
Д = 4 – 12 = – 8
Д = –1·8 = 8· i 2
Z1,2 = 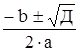 =
= 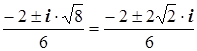
Z1,2 = 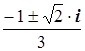
Z1 = – (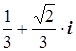 )
)
Z2 = – 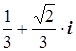
Ответ: Z1 = Z2 = – 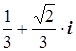
Пример 3:
Z4 – 8·Z2 – 9 = 0
Z2 = t
t2 – 8·t – 9 = 0
Д = b2 – 4·a·c = 64 + 36 = 100
t1,2 = 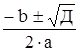 =
= 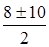 = 4
= 4 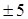
t1 = 9 t2 = – 1
Z2 = 9 Z2 = – 1
Z1,2 = 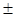 3 Z =
3 Z = 
Z3,4 = 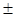 i
i
Ответ: Z1,2 = 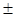 3, Z3,4 =
3, Z3,4 = 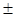 i
i
Пример 4:
Z4 + 2·Z2 – 15 = 0
Z2 = t
t2 + 2·t – 15 = 0
Д = b2 – 4·a·c = 4 + 60 = 64
t1,2 = 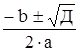 =
= 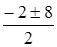 = –1
= –1 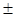 4
4
t1 = – 5 t2 = 3
Z2 = – 5 Z2 = 3
Z2 = – 1·5 Z3,4 = 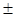
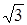
Z2 = i 2 ·5
Z1,2 = 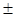 i
i 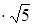
Ответ: Z1,2 = 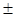 i
i 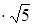 , Z3,4 =
, Z3,4 = 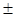
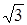
Пример 5:
Z2 = 24 – 10· i
Пусть Z = X + Y· i
(X + Y· i)2 = X2 + 2·X·Y· i –Y2
X2 + 2·X·Y· i – Y2 = 24 – 10· i
|
|
Y = – 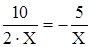
X2 – 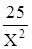 = 24
= 24
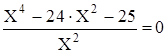 умножим на X2
умножим на X2  0
0
X4 – 24·X2 – 25 = 0
X2 = t
t2 – 24·t – 25 = 0
t1·t2 = – 25
t1 + t2 = 24
t1 = 25 t2 = – 1
X2 = 25 X2 = – 1 — нет решений
X1,2 = 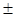 5
5
X1 = 5 X2 = – 5
Y1 = – 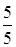 Y2 =
Y2 = 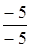
Y1 = – 1 Y2 = 1
Тогда:
Z1,2 = 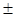 (5 – i)
(5 – i)
Ответ: Z1,2 = 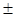 (5 – i)
(5 – i)
Date: 2015-07-02; view: 4892; Нарушение авторских прав