
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Степени мнимой единицы
|
|
Лекция 1. Комплексные числа.
Комплексные числа
Действительных чисел оказывается недостаточно для решения алгебраических уравнений.
Например: 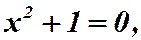 или
или  ;
; 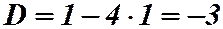 .
.
Для решения уравнения 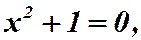 нужно ввести некоторое новое число и считать его решением этого уравнения. Будем обозначать это новое число символом i.
нужно ввести некоторое новое число и считать его решением этого уравнения. Будем обозначать это новое число символом i.
Таким образом, для числа i справедливо (так как он корень уравнения):
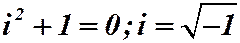 - называется мнимой единицей;
- называется мнимой единицей; 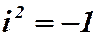 .
.
Введение мнимой единицы позволяет извлекать корни чётных степеней из отрицательных чисел.
Степени мнимой единицы
Рассмотрим степени мнимой единицы:
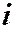
|

|
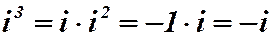
|

|
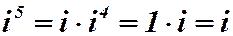
|
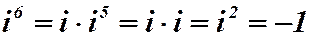
|
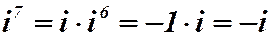
|
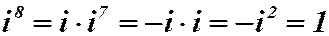
|
Если выписать все значения степеней числа 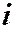 , то мы получим такую последовательность:
, то мы получим такую последовательность: 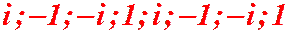 и т.д. Легко видеть, что значения степеней числа
и т.д. Легко видеть, что значения степеней числа 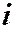 повторяются с периодом равным четырём. Таким образом, если показатель степени числа
повторяются с периодом равным четырём. Таким образом, если показатель степени числа 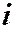 делится на четыре, то значение степени равно 1; если при делении показателя степени на четыре в остатке получается 1, то значение степени равно
делится на четыре, то значение степени равно 1; если при делении показателя степени на четыре в остатке получается 1, то значение степени равно  ; если при делении показателя степени на четыре в остатке получается 2, то значение степени
; если при делении показателя степени на четыре в остатке получается 2, то значение степени  ; если при делении показателя степени на четыре в остатке получается 3,то значение степени равно –
; если при делении показателя степени на четыре в остатке получается 3,то значение степени равно – 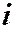 . Пользуясь этим правилом можно вычислять любую степень числа
. Пользуясь этим правилом можно вычислять любую степень числа 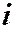 .
.
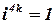
|
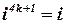
|

|
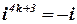
|
Определение 1.1. Комплексными числами называются выражения вида 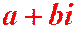 (а, b – действительные числа,
(а, b – действительные числа, 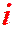 – символ) и обозначаются:
– символ) и обозначаются: 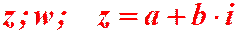 .
.
a – это действительная часть комплексного числа 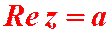 ,
,
b – это мнимая часть комплексного числа 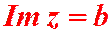 .
.
Если  , то комплексное число называется чисто мнимым, если
, то комплексное число называется чисто мнимым, если  , то комплексное число равно а, называется действительным.
, то комплексное число равно а, называется действительным.
Пример1.1. 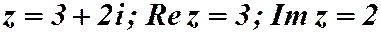 .
.
 .
.
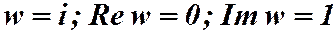 .
.
Для комплексных чисел вводятся понятия сложения, умножения и равенства:
а) Два комплексных числа 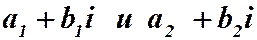 равны тогда и только тогда, когда
равны тогда и только тогда, когда 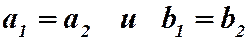 .
.
б) Суммой чисел 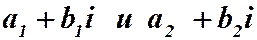 называется число
называется число 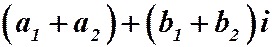 .
.
в) Произведением комплексных чисел – называется число: 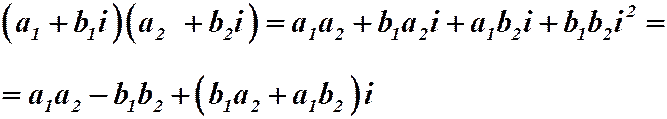
Сложение, вычитание, умножение комплексных чисел в алгебраической форме производят по правилам соответствующих действий над многочленами.
Date: 2015-07-02; view: 4116; Нарушение авторских прав