
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Классификация зажимных механизмов
Зажимные механизмы приспособлений делятся на простые и комбинированные. К простым (или элементарным) механизмам относятся клиновые, винтовые, рычажные, эксцентриковые, шарнирно-рычажные и плунжерные.
Комбинированные зажимные механизмы состоят из двух-трех последовательно сблокированных простых механизмов. Например, кли-но-рычажный, винто-рычажный и т.д.
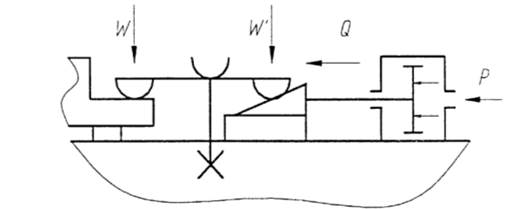
Рис. 1.42 Схема комбинированного ЗМ
При конструировании приспособления всегда возникает задача по известной силе зажима W установить тип и основные размеры зажимного механизма и рассчитать величину исходной силы Q развиваемой силовым приводом приспособления.
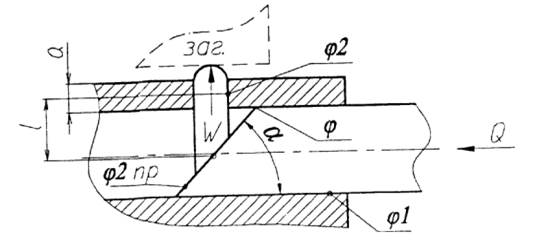
Рис. 1.43 Клиновой ЗМ
Для любого зажимного механизма можно записать уравнения сил и перемещений.
W = Qic, Sw = Sq/c, ic = W.'O, /с > /, ш = Sw/Sq, iu< 1, где /с и т - передаточные отношения сил и перемещений; зависящие от конструктивных параметров зажимного механизма.
Sq - ход силового привода, мм;
Sw - перемещение исполнительного звена зажимного механизма, мм.
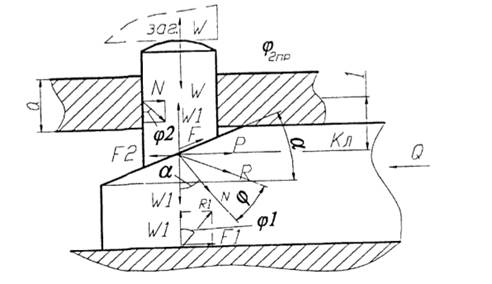
Рис. 1.44 Расчетная схема
Передаточное отношение комбинированных механизмов определяется как произведение передаточных отношений простых механизмов /k =/l,/2...m, n - число простых механизмов. т=1//с. Клиновые зажимные механизмы широко используются в приспособлениях, которые характеризуются простотой и компактностью.
Для идеального клина (рис. 1.44) iкл=l/tga, т.е. выигрыш в силе зависит от угла наклона клина а. С уменьшением угла наклона / - увеличивается, и при достижении значений а равного углу трения ср клин становится самотормозящим, т.е. можно убрать силу Q, а заготовка останется закрепленной. Угол трения определяется
φ = arctg f, (1.22)
где/ - коэффициент трения в контакте плунжера с клином, при сухом трении стали по стали f= 0,1 и φ= 6°. В реальном клиновом механизме всегда следует учитывать потери на трение (рис. 1.44). Так, для консольного плунжера имеем
ikk=(l- tg(α+φ) tg φ2np)/ (tg(α+φ) tg φl) (1.23)
где φ - угол трения на скосе клина;
φ1 - угол трения в направляющих клина;
φ2пр - угол трения в направляющих плунжера, определенный по
формуле
tgq>2np=3la/tgy2 (1.24)
Передаточное отношение по перемещению клинового механизма
определяется
in.кл=(tg(α+φ)+ tg φl)/ (l- tg(α+φ) tg φ2np) (1.25)
Для идеального клина inкл=l/iкl=tgα
Р = w l tg(α+φ)) (1.26)
Fl=wltgφl (1.27)
Q = P+F1 = w l(α+φ) +wltg φl (1.28)
Q=1/(tg(α+φ)+ tg φl)
Из условия равновесия плунжера
Р = N*F2 = Ntgφ2 - Р tgφ2 (1.30)
W= W1 -F2, F2Ntgj2 =Ptgj2
W=W1- Ptgj2 (1.31)
Для уменьшения трения и если габариты приспособления позволяют, плунжер выполняется с опорным роликом, а для выигрыша в перемещении клин выполняется с двумя углами скоса а и а1.
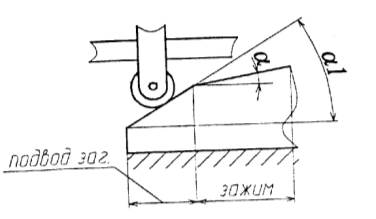
Рис. 1.45 Схема двухскосого ЗМ
При перемещении по первому скосу (al - угол) клина плунжер быстро подводится к зажимаемой заготовке; при перемещении по скосу с углом а осуществляется закрепление заготовки. Расчеты клиновых механизмов представлены - Ансеров М.А. Приспособления для металлорежущих станков, М. Машиностроение. 1975 г.
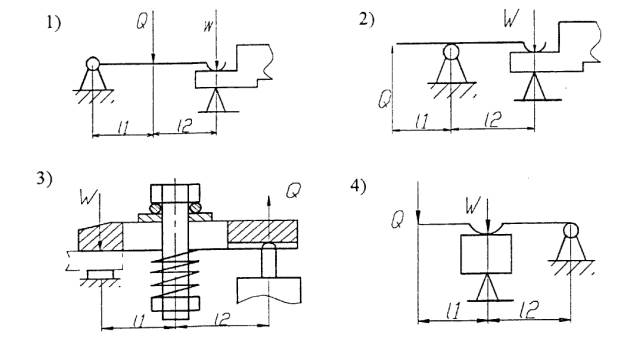
Рис. 1.46 Схемы рычажного механизма
Рычажные зажимные механизмы позволяют изменить величину и направление силы зажима. В основу их конструкции положены прямые или угловые рычаги. Конструктивных разновидностей рычажных механизмов много, однако все они сводятся к трем силовым схемам (рис. 1.46).
Пусть 11=12: a) ip = 11/11+12 = 1/2 б) ip=ll/l2 = l в) iu д=(11+12)Л1=2.
В реальных зажимных механизмах следует учитывать потери на трение которые могут достигать 6%. Трение можно учесть путем введения в расчетные формулы коэффициент полезного действия рычага равного /7 = 0,9, для схемы 1 ipM=(1l/l1+l2)η
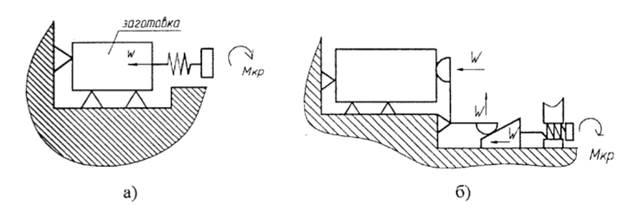
Рис. 1.47 Схемы механизмов
Винтовые механизмы используются либо (рис. 1.47а) для непостредствен-ного зажима заготовки либо входят в комплект комбинированного механизма (рис. 1.47 б).
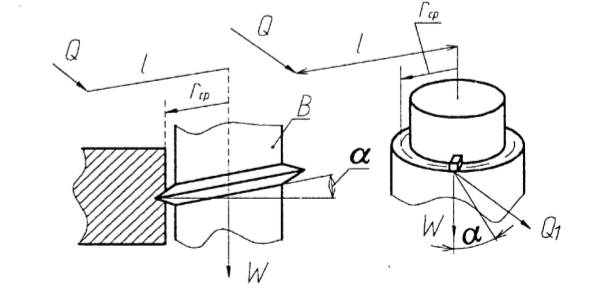
Рис. 1.48 Схема винтового механизма
Сам винтовой механизм можно рассматривать как комбинированный состоящий из рычажного с соотношениями плеч l и rср и клинового с трением по наклонной поверхности.
iид.рыч = l/ rср, i ид.кл= 1/tgα; iид.винт = 1/ rср tgα.
В реальных *" мехашгзмах учитьшается потери на трение в резьбе и тогда: iвинт = l/ rсрtg(α+φпр),где l-длина рукоятки ключа; rср - средний радиус резьбы; α - угол подъема резьбы tg α = S/2π rcp; S шаг резьбы; φпр - приведенный угол трения φпр = arctgfпp.
У механизмов с метрической и трапециидальной резьбой винт перемещается как-бы по V - образному желобу и приведенный коэффициент трения определяется fпр=f/(cosβ/ 2), гдеf- коффициент трения для плоского контакта; β/2 - половина угла при вершине профиля резьбы.
Например, для метрической резьбы с треугольным профилем
φпр=1/ cos 30=1.15f
При f =0,1 сталь по стали fnp=tgαnp =0,115 φпр = 6° 40'
У стандартных метрических и трапециидальных резьб углы подъема α =2...4 и поэтому данные резьбы являются самотормозящими.
W=2Ql/dccpt(α+φпр)=2Mkp/dccpg(α+φпр) (1.34)
Рис. 1.49 Схема эксцентрикового механизма
Эксцентриковые зажимные механизмы находят меньшее применение нежели клиновые, рычажные и винтовые, и используются в приспособлениях как с ручным зажимом так и с механизированным. Достоинством данного зажимного механизма является быстродействие. Однако экцентриковым зажимным механизмам присущ ряд недостатков:
- малая величина рабочего хода, ограниченная величиной эксцентриситета (е):
- повышенная утомляемость рабочего, так как при откреплении заготовки рабочему приходится прикладывать силу, чтобы преодолеть самоторможение эксцентрика;
- ненадежность зажима при работе с ударами и вибрациями. Эксцентриковый зажим представляет собой круглый диск, ось
вращения которого смещена относительно его центра. Эксцентрик представляет собой соединение в одной детали двух элементов: круглого диска радиусом г и криволинейного односкосого клина. При повороте вокруг оси вращения диска (точка О) клин входит как бы в зазор между диском и заготовкой и развивает силу зажима W.
Поскольку криволинейный клин имеет переменную величину наклона <х2 >ctl. то сила зажима W будет колебаться в определенных пределах в зависимости от угла поворота р экцентрика. При расчетах принимают среднее значение угла клина определяемое по формуле
tgacp = 2e/πr=2e/(π(R-e))=2E/πr; icэ=l/(r(tgαcp+φ+tgα1))
W=2Ql/D[tg(αcp+φ)+ tgα1] (1.35)
При проектировании эксцентрика необходимо определить: е - эксцентриситет; QI - момент зажима; d - диаметр оси. Известно W -требуемая сила зажима; R - радиус диска, определяется конструктивно с /четом диаметра оси. Эксцентриситет рассчитывается:
e=(π/2β)*(S1+Tн+w/it) (1.36)
где β - угол поворота эксцентрика в радианах;
S1 - минимальный зазор, обеспечивающий свободную установку заготовки с максимальным размером Ннб, мм. Диаметр оси рассчитывается:
d0 =W/b[σcм]
где b - ширина эксцентрика (задается);
[σтсм] - допускаемое напряжение на смятие материала оси ([σсм] =
= 0,5σв)
φ и φ1 - углы трения, которые можно принять при трении стали
по стали 6 градусов.
Мкр.см. = WR [tg(acp+φ) + tпφ1 (1.38)
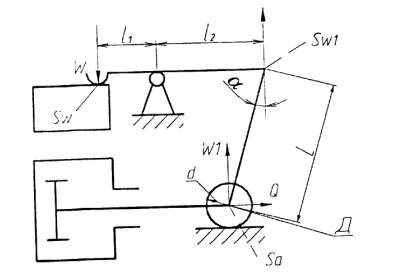
Рис. 1.50 Схема шарнирнорычажного ЗМ
Щарнирно-рычажные механизмы относятся к комбинированным ЗМ и состоят из системы рычагов. По конструкции различают одноры-чажные и двухрычажные, одностороннего и двухстороннего действия.
где
W1 =Q/(2tg(α+β))
Q - исходная сила в Н;
α - угол наклона рычага а=12...15°;
β - угол учитывающий потери на трение в шарнирах рычаг;
φ = arcsin (fd/l); (1.40)
где f = 0.1 - коэффициент трения скольжения;
d - диаметр осей шарниров;
l - длина рычага
icp = l2/icp.шp.= Wl2/(2l1 tg(α+β)) = Ql2/(2l1tg(α+β))
Date: 2015-07-01; view: 3587; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |