Вывод формулы площади произвольного четырёхугольника

S_ABCD = S_ΔAOB + S_ΔBOC + S_ΔCOD + S_ΔAOD =
= AO*OB*sinα + OB*OC*sin(π-α) + CO*OD*sinα + AO*OD*sin(π-α) =
= sinα*(AO*OB+OB*OC+CO*OD+AO*OD) =
= sinα*(OB*(AO+OC)+OD*(CO+AO)) = sinα*(OB+OD)*(AO+OC) = d1d2*sinα

31. Теорема Фалеса.
Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.

Доказательство:
Пусть точки A₁, A₂, A₃ – точки пересечения параллельных прямых с одной из сторон угла. А точки B₁, B₂, B₃ – соответствующие точки пересечения этих прямых с другой стороной угла. Докажем, что если A₁A₂ = A₂A₃, то B₁B₂=B₂B₃.

Проведем через точку В₂ прямую С₁С₂, параллельную прямой A₁A₂. Получаем параллелограммы A₁C₁BA₂ и A₂B₂C₂A₃. По свойствам параллелограмма, A₁A₂ = C₁B₂ и A₂A₃ = B₂C₂. Так как A₁A₂ = A₂A₃, то C₁B₂ = B₂C₂.

ΔC₁B₂B₁ = ΔC₂B₂B₃ по второму признаку равенства треугольников (C₁B₂ = B₂C₂, ∠ C₁B₂B₁ = ∠ C₂B₂B₃, как вертикальные,

∠B₁C₁B₂ = ∠B₃C₂B₂, как внутренние накрест лежащие при прямых B₁C₁ и C₂B₃ и секущей С₁С₂). Из равенства треугольников следует, что B₁B₂=B₂B₃. Теорема доказана.

Деление отрезка на равные части.
Из конца отрезка – точки А проведем вспомогательный луч под произвольным углом α. На этом луче отложим 4 равных отрезка произвольной длины. Конец последнего, четвертого, отрезка соединим с точкой В. Далее из всех предыдущих точек 1…3 проведем отрезки, параллельные отрезку В4 до пересечения с отрезком АВ в точках1', 2', 3'. Полученные таким образом точки разделили отрезок на равные четыре отрезка.

32. Площадь круга:
S = πR²

Площадь части круга:
В градусах:
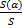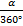= <=> S(α) =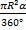
В радианах:
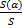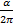= <=> S(α) = = αR²

33. Признаки прямоугольника.
Параллелограмм является прямоугольником, если:
- все его углы равны.
- его диагонали равны.

Признаки ромба.
Параллелограмм является ромбом, если:

- Две его смежные стороны равны.

- Его диагонали перпендикулярны.

- Одна из диагоналей является биссектрисой его угла.

Признаки квадрата.
Прямоугольник является квадратом, если он обладает каким-нибудь признаком ромба.

Теорема о диагоналях параллелограмма.
Если в параллелограмме диагонали являются биссектрисами его углов, то он - ромб.

Доказательство:
Для доказательства достаточно увидеть, что все четыре треугольника, на которые ромб разбивается диагоналями, равны по стороне и двум углам (противоположные углы ромба равны, значит и их половины равны). Для треугольников АВО и СВО - ВО - общая, углы АВО и СВО равны и ВАО и ВСО равны (как половины противоположных углов). Поэтому равны и их соответственные стороны, т.е. все стороны параллелограмма равны между собой.

34. Теорема о внешнем угле треугольника.
Внешний угол треугольника больше любого внутреннего, с ним не смежного.

Доказательство:
Рассмотрим треугольник АВС и какой-либо из его внешних углов, например угол, смежный с углом АСВ. Докажем, что он больше угла CВA. Проведем медиану АD и продолжим ее за точку D на такое же расстояние. Получим точку A1. Нажми и увидишь

Можно поступить и иначе: возьмем точку A1, симметричную A относительно середины ВС - точки D. Треугольник DСА1 равен треугольнику DBА (по первому признаку), откуда ∠DBА = ∠DСА1.

Но угол DСА1 меньше угла, смежного с углом АСВ, поскольку составляет его часть.
Теорема доказана.

Теорема о сумме углов треугольника.
Сумма углов треугольника на евклидовой плоскости равна 180°.

Доказательство:
Пусть ABC' — произвольный треугольник. Проведем через вершину B прямую, параллельную прямой. Отметим на ней точку D так, чтобы точки A и D лежали по разные стороны от прямой BC. Углы DBC и ACB равны как внутренние накрест лежащие, образованные секущей BC с параллельными прямыми AC и BD. Поэтому сумма углов треугольника при вершинах B и С равна углу ABD. Сумма всех трех углов треугольника равна сумме углов ABD и BAC. Так как эти углы внутренние односторонние для параллельных AC и BD при секущей AB, то их сумма равна 180°.
Теорема доказана.

35. Теорема о величине углов между касательной и хордой.
Угол между касательной к окружности и хордой, проведенной через точку касания, измеряется половиной дуги, заключенной внутри того угла.

Доказательство:
Рассмотрим меньший из углов между хордой AB и касательной к окружности в точке B. Пусть BD - диаметр окружности. Поскольку BD перпендикулярен к касательной, угол ABD дополняет до 90° рассматриваемый угол между хордой AB и касательной. Но по основной теореме о касательной угол BAD прямой.
Значит, угол ADB также дополняет до 90° угол ABD. Таким образом, рассматриваемый угол равен углу ADB и измеряется половиной указанной дуги.
Теорема доказана.

Теорема о величине угла между пересекающимися хордами.
Угол между двумя пересекающимися хордами окружности изменяется полусуммой заключённых межу ними дуг.

Доказательство:
Достроить треугольник BED.
Нас интересует величина угла AED, образованного пересекающимися в точке E хордами AB и CD. Поскольку угол AED – внешний угол треугольника BED, а углы CDB и ABD являются вписанными углами, то справедливы равенства:
α = ∠AED = ∠CDB + ∠ABD = β + γ =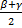

Теорема доказана.

Теорема о величине угла между секущими.
Угол между двумя секущими, которые пересекаются вне окружности, измеряется полуразностью заключённых между ними дуг.

Доказательство:
Достроить хорды крест-накрест.
Нас интересует величина угла BED, образованного пересекающимися в точке E секущими AB и CD. Поскольку угол ADC – внешний угол треугольника ADE, а углы ADC, DCB и DAB являются вписанными углами, то справедливы равенства:
α = ∠BED = ∠ADC + ∠DAB = β – γ =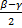

Что и требовалось доказать.

36. Свойство описанного четырёхугольника.
В описанном четырёхугольнике суммы противоположных сторон равны.

Доказательство:
Пусть четырёхугольник ABCD описан около окружности, т. е. стороны его АВ, ВС, CD и DA — касательные к этой окружности.
Требуется доказать, что АВ + CD =AD + ВС. Обозначим точки касания буквами М, N, К, Р. На основании свойств касательных, проведённых к окружности из одной точки, имеем:

АР = АК;

ВР = ВМ;

DN = DK;

CN = СМ.
Сложим почленно эти равенства. Получим:
АР + ВР + DN + CN = АК + ВМ +DK + СМ,

т. е. АВ + CD = AD + ВС, что и требовалось доказать.

37. Свойства параллельных прямых.
1. Если одна из пары параллельных прямых параллельна третьей прямой, то и другая прямая параллельна третьей прямой.

2. В одной плоскости с заданной прямой через точку, лежащую вне прямой, можно провести только одну прямую, параллельную заданной прямой.

3. Если две прямые на плоскости перпендикулярны третьей прямой, то они параллельны.

Теорема об углах, образованных двумя параллельными прямыми и секущей.
1. Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.

2. Если две параллельные прямые пересечены секущей, то соответственные углы равны.

3. Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°.

Доказательство:
Пусть параллельные прямые a и b пересечены секущей c. Докажем, что накрест лежащие углы 3 и 6 равны. Допустим, что углы 3 и 6 не равны. Отложим от луча а угол α, равный углу 6, так, чтобы угол α и угол 6 были накрест лежащими углами при пересечении прямых а₁ и b секущей с. По построению эти накрест лежащие углы равны, поэтому МР||b. Мы выяснили, что через точку М проходят две прямые (прямые a и а₁), параллельные прямой b. Но это противоречит аксиоме параллельных прямых. Значит, наше допущение неверно и угол 3 равен углу 6.

Следствия из теоремы:
1. Если каждая из двух прямых АВ и СD параллельна одной и той же третьей прямой МN, то первые две параллельны между собой.
В самом деле, проведя секущую ЕF (черт. 206), получим:

а) ∠1 = ∠3, так как АВ || МN;
б) ∠2 = ∠3, так как СО || МN.я
Значит, ∠1 = ∠2, а это соответственные углы при прямых АВ и СD и секущей ЕF, следовательно, прямые АВ и СD параллельны.

2. Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой.
В самом деле, если ЕF ⏊ АВ, то ∠1 = d; если АВ || СD, то ∠1 = ∠2.
Следовательно, ∠2 = d т. е. ЕF ⏊ СD.

38. Вывод уравнения прямой.
Получим сначала уравнение прямой, проходящей через заданную точку M0(x0; y0) перпендикулярно данному
ненулевому вектору N{a;b}. Отметим на прямой точку M(x; y). Поскольку векторы N⏊M₀M, то N*M₀M = 0
a (x – x₀) + b (y – y₀) = 0 – уравнение прямой, проходящей через заданную точку перпендикулярно данному вектору.
Вектор N{a;b} называется нормальным вектором этой прямой.
ax - ax₀ + by – by₀ = 0
ax + by + (- ax₀ – by₀) = 0
ax + by + c = 0, где a, b и c – произвольные числа, причем a² + b² ≠ 0

Уравнение прямой, проходящей через данную точку с данным угловым коэффициентом:
y = k(x – x₀) + y_0.

Взаимное расположение прямой и окружности.
1. Прямая пересекает окружность в двух точках.
2. Прямая касается окружности.
3. Прямая не имеет общих точек с окружностью.

39. Признак описанного четырёхугольника.
Выпуклый четырехугольник называется описанным, когда суммы длин его противолежащих сторон равны.

Доказательство:
Необходимость. Пусть четырехугольник ABCD описанный, и M, P, L, N – точки касания его сторон. Имеем BM = BN, CM = CP, DP = DL, AL = AN (отрезки касательных, проведенных из одной точки равны). Отсюда BM + MC + AL + LD = BN + AN + CP + PD.
Достаточность. Пусть в четырехугольнике ABCD выполнено равенство AB + CD = BC + AD. Биссектрисы углов ∠BAD и ∠ABC пересекаются в точке O. Точка O одинаково удалена от прямых AB, BC и AD. Пусть ω(О, r) – окружность, касающаяся сторон AB, BC и AD, а сторона CD пересекает окружность ω. Проведем касательную к окружности ω из точки C, и пусть она пересекает прямую AD в точке D₁. Тогда из необходимого условия – AB + CD₁ = BC + AD₁. Вычитая из данного равенства равенство в условиях теоремы получаем CD₁ – CD = AD₁ – AD или CD₁ – CD = DD₁, CD₁ = CD + DD₁. Мы пришли к противоречию, так как CD₁ < CD + DD₁. В случае, если прямая CD не пересекает окружность ω, доказательство аналогично.
Теорема доказана.

40. Свойство прямоугольника.
Диагонали прямоугольника равны.

Свойство ромба.
Диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов.

Свойства квадрата.
1. Все свойства прямоугольника и ромба.
2. Диагонали квадрата равны a .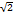

Теорема о диагоналях ромба.
Диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов.

Доказательство:
Пусть ABCD – данный ромб. Диагонали ромба пересекаются в точке O.

По свойству параллелограмма AO = OC, значит BO – медиана Δ ABC. А так как треугольник ABC - равнобедренный, то по свойствам медианы равнобедренного треугольника проведенной к основанию, BO является также высотой и биссектрисой.
Значит прямая BO ⊥ AC и ∠ ABO = ∠ CBO.
Теорема доказана.

41. Вывод формулы для нахождения координаты точки, делящей отрезок пополам.
Пусть в системе координат Oxy точка А имеет координаты (x1;y1), а точка В – координаты (x2;y2).
Выразим координаты (x;y) середины С отрезка АВ через координаты его концов.
Так как точка С – середина отрезка АВ, то
OC = (OA+OB).
Координаты векторов ОС, ОА и ОВ равны соответствующим кординатам точек С, А и В:
OC {x;y}, OA {x1;y1}, OB {x2;y2}.
Записывая равенство в координатах, получим:
,
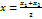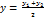
Таким образом, каждая координата середины отрезка равна полусумме соответствующих координат его концов.

42. Вывод формулы радиуса вписанной в прямоугольный треугольник окружности.
Поскольку четырёхугольник CDOF является прямоугольником, у которого соседние стороны DO и OF равны, то этот прямоугольник – квадрат. Следовательно, CD = CF = r,
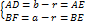=> c = AE + BE = b – r + a – r = a + b – 2r.
Следовательно, принимая во внимание теорему Пифагора, получаем:
r = (a + b – c)

Вывод формулы радиуса описанной около прямоугольного треугольника окружности.
Построить симметрично такой же треугольник.
Центр описанной окружности прямоугольника лежит на пересечении его диагоналей.
По свойству параллелограмма диагонали точкой пересечения делятся пополам.
По свойству прямоугольника диагонали равны.
Следовательно, радиус описанной около прямоугольного треугольника окружности равен половине гипотенузы.
R = c.

43. Вывод числовых значений синуса, косинуса и тангенса.
Построить прямоугольный треугольник с углами 90, 45, 45 и с углами 90, 60, 30.

44. Признаки и свойства прямоугольного треугольника.
Признаки:
1. Если квадрат одной из сторон треугольника равен сумме квадратов двух других сторон, то такой треугольник прямоугольный.
2. Если медиана треугольника равна половине соответствующей ей стороны, то треугольник прямоугольный.
Свойства:
1. Медиана, проведенная к гипотенузе прямоугольного треугольника, равна половине гипотенузы.
2. В прямоугольном треугольнике центр описанной окружности лежит на стороне треугольника и совпадает с серединой гипотенузы.

45. Свойство биссектрисы угла треугольника.
Биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам.

Доказательство:
Проведем через B прямую, параллельную AC, и обозначим через D точку пересечения этой прямой с продолжением AA ₁.
Согласно свойству параллельных прямых имеем ∠BDA = ∠CAD. Так как AA ₁ - биссектриса, то ∠CAD = ∠DAB. Итак, ∠BDA =∠DAB, потому BD = BA. Из подобия треугольников CAA ₁ и BDA ₁ (по второму признаку ∠BDA ₁ = ∠CAA ₁, ∠BA ₁ D = ∠CA ₁ A) получаем
= =

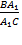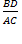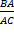
46. Свойства биссектрис углов параллелограмма.
Биссектрисы соседних углов параллелограмма перпендикулярны.

Доказательство:
Пусть BM и CK — биссектрисы углов параллелограмма, прилежащих к стороне BC. Сумма углов ABC и BCD равна 180°. Углы OBC и OCB — половинки углов ABC и BCD. Значит, сумма углов ABC и BCD равна 90 градусов. Из треугольника BOC находим, что угол BOC — прямой.
Теорема доказана.