Алгебра множеств

Современная математика определяет алгебру как совокупность объектов, над которыми можно производить действия (операции). Рассматривая множества как объекты, некоторым образом соответствующие действия сложения и умножения в алгебре чисел. При этом сохраняют силу основные законы алгебры чисел:

- переместительный (коммутативный):

, ;

- сочетательный (ассоциативный):

, ;

- распределительный (дистрибутивный):

.

Рассмотрим основные операции алгебры множеств.

Пересечение множеств А и В есть множество, состоящее из тех и только тех элементов, которые принадлежат и множеству А, и множеству В (Рис. 1.4). Обозначается пересечение .

Пример 1.3. Если А – множество четных чисел, а В множество целых положительных чисел, меньших 10, то

.

Пример 1.4. Пусть А – множество вольтметров в лаборатории, В – множество цифровых приборов в лаборатории, тогда - множество цифровых вольтметров.

Пересечение нескольких множеств обозначается: .

Пересечение множеств подчиняется:

- переместительному закону - ,

- сочетательному закону - .

Если множества А и В не имеют общих элементов, то они называются непересекающимися, и для них справедливо соотношение .

Так, в примере 1.4 множество цифровых вольтметров может оказаться пустым.

Операция пересечения имеет некоторую аналогию с умножением, поскольку элементы результирующего множества обладают свойствами множеств-сомножителей. Это подтверждается и соотношением , аналогично .

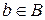Прямое (декартово) произведение множеств А и В есть множество всех упорядоченных пар или кортежей , у которых и . Обозначается А В.

Пример 1.5. Пусть А , . Тогда . Множество А В состоит из 64 кортежей и содержитобозначения всех 64 клеток шахматной доски.

Пример 1.6. Если Х и У представляют собой отрезки вещественных осей (то есть линейные точечные множества), то прямое произведение Х У определяется совокупностью всех точек заштрихованного прямоугольника на Рис. 1.5.

Аналогично прямым произведением множеств будет множество кортежей длины n вида

.

Очевидно, что вследствие упорядоченности своих элементов прямое произведение не обладает переместительным свойством, то есть .

Прямое произведение одинаковых множеств называется степенью множества. Если , то

При этом считается, что и .

Если в примере 1.6 принять , где R – множество всех вещественных чисел, то является множеством всех точек вещественной плоскости. Аналогично представляет собой трехмерное пространство, а 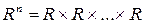- n – мерное пространство, называемое также гиперпространством.

По аналогии с нахождением проекций кортежей векторов можно осуществить операцию построения любого множества, состоящего из кортежей одинаковой длины. Проекцией такого множества является множество проекций входящих в него кортежей.

Если V – множество v, то проекцией множества будет множество проекций кортежей, то есть .

Пример 1.7. Для множества кортежей 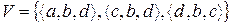определим проекции

Пример 1.8. Пусть . Тогда для

Из примера 1.8 видно, что . Можно показать, что для , получим .

Объединение множеств А и В есть множество, состоящее из элементов, которые принадлежат или множеству А, или множеству В (Рис. 1.6).

Обозначается объединение . Имеется аналогия с операцией суммирования, но неполная, так как объединение может сопровождаться пересечением (Рис. 1.6б).

Пример 1.9. Если А – множество студентов группы, занимающихся спортом во время каникул, а В – множество студентов группы, регулярно тренирующихся в спортивных секциях, то - множество студентов-спортсменов. Часть из них может относиться и к тем, и к другим.

Объединение нескольких множеств записывается как .

Операция объединения множеств подчиняется:

- переместительному закону - ,

- сочетательному закону - .

Для пустого множества имеем (аналогия ).

Систему подмножеств, объединение которых дает некоторое множество М, называют разбиением множества М, если все подмножества – непересекающиеся, то есть попарные пересечения подмножеств пусты.

Пример 1.10. В высшей лиге футбола играют n команд, - множества футболистов, объединенных в команды. Система является разбиением множества всех футболистов высшей лиги. Каждый футболист из множества может играть только в одной команде.

Разность множеств А и В есть множество всех тех и только тех элементов множества А, которые не содержатся в множестве В (Рис. 1.7). Обозначается операция А\В и возможна только для двух множеств (строго двухместная операция).

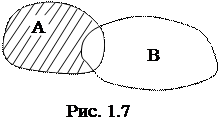Пример 1.11. Если А – множество амперметров, а В – множество измерительных приборов постоянного тока, то А\В – множество амперметров переменного тока.

Некоторое фиксированное множество, полностью содержащее все возможные для него подмножества, называется полным, или универсальным. Если пустое множество в алгебре множеств выполняет роль нуля, то универсальное множество выполняет роль единицы и обозначается I. Графически оно представляется в виде прямоугольника. Изображения множеств в виде областей внутри прямоугольника I называют диаграммами Эйлера-Венна (Рис. 1.8).

Свойства универсального множества:

1) (аналогично ),

2) , (в алгебре чисел аналогично выражению не имеет смысла).

Множество , определяемое как разность универсального множества и множества А, называется дополнением множества А, .

На Рис. 1.9 дополнение заштриховано.

Пример 1.12. Во всех предыдущих примерах со студентами множество студентов группы может рассматриваться как универсальное множество I. Если А – множество стипендиатов в группе, то будет множество студентов неполучающих стипендию.

Свойства дополнения:

1) , так как А и не имеют общих элементов,

2) , так как все элементы I принадлежат либо А, либо ,

3) если является дополнением А, то можно считать и А дополнением множества , с другой стороны, дополнение множества есть , отсюда .

Выше отмечалось, что в алгебре множеств действуют переместительный и сочетательный законы. Рассмотрим диаграммы Эйлера-Венна для распределительного закона (Рис. 1.10).

Выделенная жирной линией область соответствует правой и левой стороне записи формулы распределительного закона

,

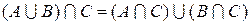что в алгебре чисел соответствует соотношению (a+b)c=ac+bc. В обычной алгебре распределительный закон, в отличие от переместительного и сочетательного, не симметричен относительно умножения и сложения. Действительно, замена знаков плюс на умножение и наоборот приводит к абсурду: ab+c=(a+c)(b+c). Применительно к множествам взаимная замена знаков и дает в обоих случаях одинаковые множества. На диаграмме 1.11 эти множества выделены жирной линией. Из этого следует, что

.

Таким образом, в алгебре множеств все три закона оказываются симметричными по отношению к действиям объединения и пересечения.

На рис. 1.12 изображены множества А и В, содержащиеся в универсальном множестве I. Из этого рисунка можно вывести, что

Теперь рассмотрим объединение и его дополнение, отсюда следует, что

.

Полученные два выражения называются тождествами или правилами де Моргана.

Контрольные вопросы

1) Как выполняется операция пересечения множеств?

2) Как выполняется операция прямого произведения множеств?

3) Как выполняется операция объединения множеств?

4) Как выполняется операция вычитания множеств?

5) Как формируется диаграмма Эйлера-Венна?

6) Как определяется универсальное множество и дополнение множества?

7) Как доказываются при помощи диаграмм Эйлера-Венна основные законы алгебры множеств?

Date: 2016-02-19; view: 616; Нарушение авторских прав