
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Примеры решения задач. Задача 11. Угол преломления луча в жидкости 35˚
Задача 11. Угол преломления луча в жидкости 35 ˚. Определить показатель преломления жидкости, если известно, что отраженные лучи максимально поляризованы.
| Дано: b = 35˚ | Решение
По закону преломления 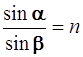 . .
|
| n –? | По условию задачи отраженные лучи полностью поляризованы, следовательно, применим закон Брюстера |
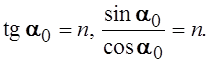
Сравнивая с предыдущей формулой, видим, что
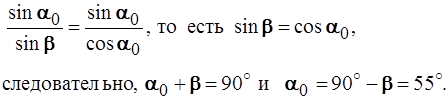
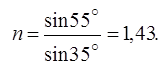
Ответ: n =1,43.
Задача 12. Естественный свет падает на систему из трех последовательно расположенных одинаковых поляроидов, причем плоскость пропускания среднего поляроида составляет угол 60 ˚ с плоскостью пропускания двух других поляроидов. Каждый поляроид обладает таким поглощением, что при падении на него линейно поляризованного света максимальный коэффициент пропускания составляет 0,81. Во сколько раз уменьшится интенсивность света после прохождения этой системы?
| Дано: a = 60˚ t = 0,81 | Решение При падении естественного света на идеальный поляроид через него проходит свет, интенсивность которого J p= ½· J ест. |
| J ест/ J –? | Но этот поляроид пропускает только долю, равную t от |
этой интенсивности, то есть J p = t×½· J ест. По закону Малюса интенсивность света, прошедшего второй поляроид
J 1 = J p cos 2 a = (t /2)×cos 2 a.
Но второй поляроид тоже не идеальный и пропускает часть, равную t от J 1:
J 1 = (t 2 /2) J ест ×cos 2 a.
Свет интенсивности J 1 падает на третий поляризатор, который тоже пропускает часть t от интенсивности идеального поляризатора
J 2 = t J 1 ×cos 2 a = J ест ×(t 3 / 2) ×cos 4 a.
Отклонение интенсивности J ест, входящей в систему, к интенсивности J 2, выходящей из системы, равно
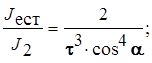
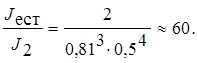
Ответ: в 60 раз.
Задача 13. На пути частично поляризованного света поместили поляризатор. При повороте поляризатора на угол a=60 ˚ из положения, соответствующего максимуму пропускания, интенсивность прошедшего света уменьшилась в h=3,0 раза. Найти степень поляризации падающего света.
| Дано: a=60˚ h=3 | Решение
Максимум пропускания соответствует случаю, когда плоскость, в которой преимущественно колеблется вектор 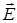 частично поляризованной волны, параллельна плоскости пропускания поляризатора. Поляризатор частично поляризованной волны, параллельна плоскости пропускания поляризатора. Поляризатор
|
| Р –? | полностью пропускает поляризованный свет и половину интенсивности естественного света |
J 1 = J n + ½· J е .
При повороте поляризатора из этого положения на 60 ˚, интенсивность пропущенного поляризованного света определится по закону Малюса, а интенсивность пропущенного естественного света будет равна, как и в первом случае, ½· J е, то есть
J 2 = J n ×cos 2 a + ½· J е.
По условию задачи J 1 / J 2 =h или J 1 = h J 2.
J n + ½· J е = 3 × (J n ×cos 2 a + ½· J е);
J n + ½· J е = 3 J n ×cos 2 60° + 3/2· J е;
¼· J n = J е, Þ J n = 4 J е.
Степень поляризации частично поляризованного света определяется формулой
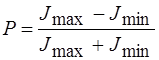
Максимальная интенсивность
J max = J 1 = J n + ½· J е =4 J е + ½· J е = 4,5 J е .
Минимальная интенсивность соответствует случаю, когда поляризатор не пропустит поляризованный свет; через него пройдет только половина поляризованного света J min = 0,5 J е .
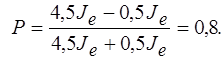
Ответ: P =0,8.
Задача 14. Плоско поляризованный монохроматический свет падает на идеальный поляризатор и полностью гасится им. Когда на пути пучка поместили кварцевую пластинку, интенсивность света стала равна половине интенсивности света, падающего на поляризатор. Определить толщину кварцевой пластинки, если постоянная вращения кварца 48,9˚град/мм.
| Дано: J 2= 1/2 J 1 a=48,9 град/мм | Решение Так как поляризованный свет гасится поляризатором, то это означает, что его плоскость пропускания перпендикулярна плоскости колебаний поляризованного света |
| d –? | (g = p / 2). |
Кварц – это оптически активное вещество, и при введении кварцевой пластинки происходит поворот плоскости колебаний на угол j = a × d, где d – толщина пластинки.
Это приводит к тому, что угол между плоскостью пропускания и новой плоскостью колебаний падающего на поляризатор поляризованного света станет равным b = p/2 – j.
По закону Малюса J 2 = J 1 ×cos 2 (p/2 – j) = ½· J 1 ;
sin 2 j = 1/2; sin 2 j = 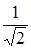 ; j = 45°.
; j = 45°.
d = j / a = 45/48,9 = 0,92 (мм).
Ответ: d = 0,92 (мм).
Date: 2015-05-18; view: 22514; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |