На пути к комплексным числам

В 1494 году учёный, францисканский монах (Италия) Лука Пачиоло (1445 – 1514) напечатал в Венеции труд “ Сумма, арифметика, геометрия и пропорциональности”, который закончил выводом: “ Решение кубических уравнений вида x3 + px = q, p > 0, q > 0, столь же невозможно при современном состоянии науки, как и решение квадратуры круга циркулем и линейкой”.

Несмотря на это предупреждение, за решение кубического уравнения взялись одновременно сразу два математика, Джеронимо Кардано (1501 – 1576) из Милана и Николо Тарталья (1506 – 1559) из Вероны. Причём первый из них получил аналитический результат, решая квадратное уравнение (слайд 3).

Он поставил задачу: нарезать участок земли прямоугольной формы с площадью 40 кв. ед. и периметром 2р = 20 лин. ед. Решая систему он пришёл к уравнению x2 - 10x + 40 = 0, корни которого не являются действительными числами. Он показал, что система уравнений не имеющая решений во множестве действительных чисел, имеет решения вида 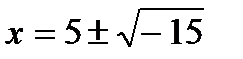, 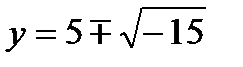. Кардано был удивлён таким результатом, назвав число софистическим, добавив, что “ для осуществления таких действий нужна была бы новая арифметика, которая была бы настолько же утончённой, насколько бесполезной”, нужно только условиться действовать над такими выражениями по правилам обычной алгебры и считать что . Итальянский алгебраист Дж. Кардано в 1545 г. предложил ввести числа новой природы.

В 1572 году замечательный учёный из Болоньи Рафаэли Бомбелли (1530 – 1572) в своём труде “ Алгебра” показывает, что при некоторых операциях над новыми числами результатом является действительное число, например: 1) 2)

3) (слайд 4)

Только в X V I I I веке величайший математик Леонард Эйлер (1707 – 1783) в работе “ Введение в математический анализ” (1746) вводит обозначение мнимой единицы: , взяв первую букву слова imaginеi res (от названия введённого Р. Декартом (1596 – 1650)) и записывает свои знаменитые формулы: exi = cosx + isinx, e-xi = cosx - isinx, из которых получает соответственно: (слайд 5)

Карл Гаусс (1777 – 1855), немецкий учёный, “ король математики”, впервые называет числа комплексными (от латинского c o m p l e k s – объединение), вводит обозначение а + b i и представляет их в виде точек плоскости. (слайд 6)

В XVI веке в связи с изучением кубических уравнений оказалось необходимым извлекать квадратные корни из отрицательных чисел. В формуле для решения кубических уравнений вида кубические и квадратные корни: .

Эта формула безотказно действует в случае, когда уравнение имеет один действительный корень ( x=1), а если оно имеет три действительных корня ( x₁=1 x_2,3 = ), то под знаком квадратного корня оказывалось отрицательное число. Получалось, что путь к этим корням ведет через невозможную операцию извлечения квадратного корня из отрицательного числа. Вслед за тем, как были решены уравнения 4-й степени, математики усиленно искали формулу для решения уравнения 5-й степени. Но Руффини (Италия) на рубеже XVIII и XIX веков доказал, что буквенное уравнение пятой степени нельзя решить алгебраически; точнее: нельзя выразить его корень через буквенные величины a, b, c, d, e с помощью шести алгебраических действий (сложение, вычитание, умножение, деление, возведение в степень, извлечение корня).

В 1830 году Галуа (Франция) доказал, что никакое общее уравнение, степень которого больше чем 4, нельзя решить алгебраически. Тем не менее, всякое уравнение n-й степени имеет (если рассматривать и комплексные числа) n корней (среди которых могут быть и равные). В этом математики были убеждены еще в XVII веке (основываясь на разборе многочисленных частных случаев), но лишь на рубеже XVIII и XIX веков упомянутая теорема была доказана Гауссом.

Date: 2015-12-11; view: 738; Нарушение авторских прав