Алгебраїчні фрактали

Це найбільша група фракталів. Отримують їх за допомогою нелінійних процесів в n -мірних просторах. Найбільше вивчені двомірні процеси. Інтерпретуючи нелінійний ітераційний процес, як дискретну динамічну систему, можна користуватися термінологією теорії цих систем: фазовий портрет, сталий процес, аттрактор і т.д.

Відомо, що нелінійні динамічні системи володіють декількома стійкими станами. Той стан, в якому опинилася динамічна система після деякого числа ітерацій, залежить від її початкового стану. Тому кожен стійкий стан (або як говорять – аттрактор) володіє деякою областю початкових станів, з яких система обов’язково потрапить в дані кінцеві стани. Таким чином, фазовий простір системи розбивається на області тяжіння аттракторів. Якщо фазовим є двомірний простір, то забарвлюючи області тяжіння різними кольорами, можна отримати колірний фазовий портрет цієї системи (ітераційного процесу). Міняючи алгоритм вибору кольору, можна отримати складні фрактальні картини з химерними багатоколірними узорами. Несподіванкою для математиків стала можливість за допомогою примітивних алгоритмів породжувати дуже складні нетривіальні структури.

Як приклад, розглянемо множину Мандельброта (pис. 13, 14). Алгоритм його побудови достатньо простий і заснований на простому ітеративному виразі:

Z [ i +1]= Z [ i ]* Z [ i ]+ C, (1)

де Z [ i ]і C – комплексні змінні. Ітерації виконуються для кожної стартової точки C прямокутної або квадратної області – підмножини комплексної площини. Ітераційний процес продовжується до тих пір, поки Z [ i ]не вийде за межі кола радіусу 2, центр якої лежить в точці (0,0) (це означає, що аттрактор динамічної системи знаходиться в нескінченності) або після достатньо великого числа ітерацій (наприклад, 200–500) Z [ i ]зійдеться до якої-небудь точки кола. Залежно від кількості ітерацій, в перебігу яких Z [ i ]залишалася усередині кола, можна встановити колір точки C (якщо Z [ i ]залишається усередині кола протягом достатньої великої кількості ітерацій, ітераційний процес припиняється і ця точка растру забарвлюється в чорний колір).

Рис. 13. Множина Мандельброта

Рис. 14. Ділянка межі множини Мандельброта, збільшена в 200 разів

Вищеописаний алгоритм дає наближення до так званої множини Мандельброта. Множині Мандельброта належать точки, які протягом нескінченного числа ітерацій не йдуть в нескінченність (точки мають чорний колір). Точки, що належать межі множини (саме там виникають складні структури) йдуть в нескінченність за кінцеве число ітерацій, а точки за межами множини, йдуть в нескінченність через декілька ітерацій (білий фон).

Розглянемо ще множину Жюліа, що утворюється за тією ж самою формулою (1), що й множина Мандельброта. Множину Жюліа було винайдено французьким математиком Гастоном Жюліа. Досить дивно, але існують різні типи цієї множин. При малюванні фрактала з використанням різних початкових точок (щоб почати процес ітерацій), генеруються різні зображення. Це може бути застосоване тільки до множини Жюліа.

Вигляд множини Жюліа залежить від значення параметра С. На рис. 15, а зображено множину Жюліа для С =0,27334+0,00742 і, а на рис. 15, б для С =-1,25.

Якщо 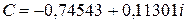, то множина Жюліа перетворюється в цікаву ламану лінію (рис. 15, в). Казковим килимом стає множина Жюліа для С = і (рис. 15, г).

а б

в г

Рис. 15. Множина Жюліа з різними параметрами С

Date: 2015-10-18; view: 1374; Нарушение авторских прав