
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Основные теоремы дифференциального исчисления
Методические указания к проведению лекционного занятия
Тема № 3.2. Основные теоремы дифференциального исчисления.
Правило Лопиталя
План:
1. Основные теоремы дифференциального исчисления
2. Правило Лопиталя
3. Раскрытие неопределённостей
Основные теоремы дифференциального исчисления
Теорема Ферма. Если дифференцируемая на промежутке Х функция 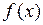 достигает наибольшего или наименьшего значения во внутренней точке
достигает наибольшего или наименьшего значения во внутренней точке 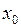 этого промежутка, то производная функции в этой точке равна нулю, т.е.
этого промежутка, то производная функции в этой точке равна нулю, т.е. 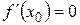 .
.
Теорема Ролля. Пусть функция 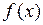 непрерывна на отрезке
непрерывна на отрезке 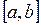 , дифференцируема на интервале
, дифференцируема на интервале 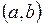 и
и 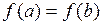 . Тогда существует точка
. Тогда существует точка 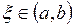 такая, что
такая, что 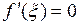 .
.
Геометрический смысл теоремы Ролля. Если выполняются все условия теоремы Ролля, то в точке 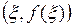 , где
, где 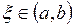 , касательная к кривой
, касательная к кривой 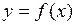 параллельна оси
параллельна оси 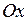 . На интервале
. На интервале 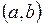 может быть несколько точек
может быть несколько точек 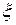 таких, что
таких, что 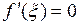 (рис. 1).
(рис. 1).
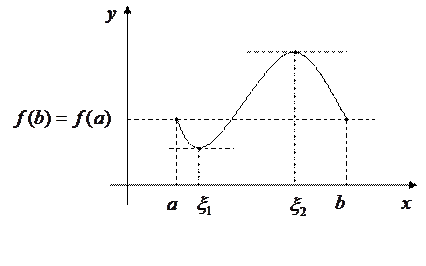 |
Рис. 1. Геометрический смысл теоремы Ролля
Пример. Проверить выполнение условий теоремы Ролля для функции 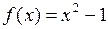 на отрезке
на отрезке 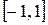 и найти соответствующие значения
и найти соответствующие значения 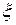 .
.
Решение. Очевидно, что, функция 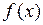 непрерывна на отрезке [-1, 1], дифференцируема на интервале (-1,1) (
непрерывна на отрезке [-1, 1], дифференцируема на интервале (-1,1) (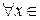 (-1,1) существует
(-1,1) существует 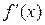 =2 x);
=2 x); 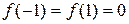 , т.е. все условия теоремы Ролля выполнены. Следовательно, найдется хотя бы одна точка
, т.е. все условия теоремы Ролля выполнены. Следовательно, найдется хотя бы одна точка 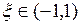 , для которой
, для которой 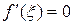 . Из уравнения
. Из уравнения 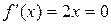 определим единственную точку
определим единственную точку 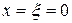 . В точке
. В точке 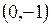 касательная к кривой
касательная к кривой 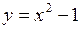 параллельна оси
параллельна оси 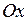 (рис. 2).
(рис. 2).
Следствие из теоремы Ролля. Если функция 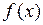 на отрезке
на отрезке 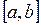 удовлетворяет условиям теоремы Ролля, причем
удовлетворяет условиям теоремы Ролля, причем 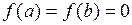 , то существует точка
, то существует точка 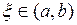 такая, что
такая, что 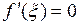 . Другими словами, между двумя нулями дифференцируемой функции лежит по крайней мере один нуль её производной.
. Другими словами, между двумя нулями дифференцируемой функции лежит по крайней мере один нуль её производной.
 |
Теорема Лагранжа. Пусть функция 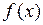 непрерывна на отрезке
непрерывна на отрезке 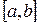 и дифференцируема на интервале
и дифференцируема на интервале 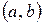 . Тогда существует точка
. Тогда существует точка 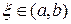 такая, что справедливо равенство
такая, что справедливо равенство
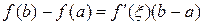 ,
, 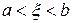 . (1)
. (1)
Доказательство. Рассмотрим вспомогательную функцию
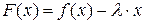 . (2)
. (2)
Определим 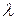 из условия
из условия 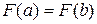 , или
, или 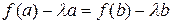 .
.
Отсюда
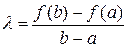 . (3)
. (3)
Функция 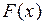 удовлетворяет всем условиям теоремы Ролля (проверьте самостоятельно), поэтому существует точка
удовлетворяет всем условиям теоремы Ролля (проверьте самостоятельно), поэтому существует точка 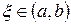 такая, что
такая, что 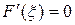 . Из формулы (2)
. Из формулы (2) 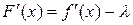 . Следовательно,
. Следовательно,  . Отсюда
. Отсюда 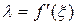 . Подставляя найденное значение
. Подставляя найденное значение 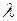 в (3), получим
в (3), получим
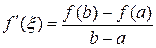 (4)
(4)
или 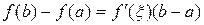 . Теорема доказана.
. Теорема доказана.
Формула (1) называется формулой Лагранжа или формулой конечных приращений.
Геометрический смысл теоремы Лагранжа. Правая часть равенства (4) есть тангенс угла наклона угла хорды 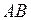 , стягивающей конечные точки графика функции
, стягивающей конечные точки графика функции 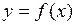 на отрезке
на отрезке 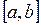 , к положительному
, к положительному 
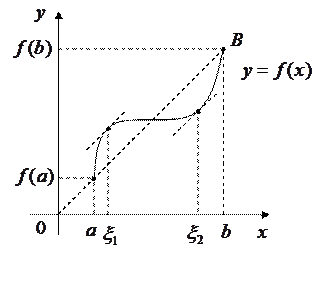 |
направлению оси абсцисс (рис. 3).
Левая часть этого равенства равна тангенсу угла наклона касательной к графику 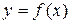 в некоторой промежуточной точке
в некоторой промежуточной точке 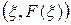 , где
, где 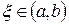 .
.
Таким образом, теорема Лагранжа утверждает, что, если функция 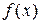 на отрезке
на отрезке 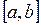 удовлетворяет условиям теоремы, то найдется хотя бы одна точка
удовлетворяет условиям теоремы, то найдется хотя бы одна точка 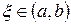 такая, что касательная к кривой в точке
такая, что касательная к кривой в точке 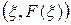 параллельна хорде, стягивающей концы кривой
параллельна хорде, стягивающей концы кривой 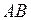 . Из рис. 3 видно, что в данном случае условиям теоремы удовлетворяют две точки:
. Из рис. 3 видно, что в данном случае условиям теоремы удовлетворяют две точки: 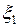 и
и 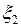 .
.
|
Замечание. Теорему Лагранжа называют также теоремой о среднем, так как она определяет значение функции в некоторой промежуточной (“средней”) точке ξ интервала 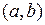 .
.
Пример. Проверить выполнение теоремы Лагранжа для функции 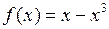 на отрезке
на отрезке 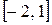 и найти соответствующие значения ξ.
и найти соответствующие значения ξ.
Решение. Очевидно, что функция 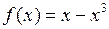 непрерывна на отрезке
непрерывна на отрезке 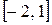 и дифференцируема на интервале (-2, 1), т. к. при любых
и дифференцируема на интервале (-2, 1), т. к. при любых 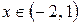 существует
существует 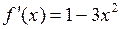 . Условия теоремы Лагранжа выполнены. Следовательно, на интервале
. Условия теоремы Лагранжа выполнены. Следовательно, на интервале 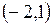 найдется хотя бы одна точка ξ, для которой справедливо равенство
найдется хотя бы одна точка ξ, для которой справедливо равенство 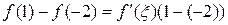 . Так как
. Так как 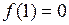 ,
, 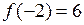 , то
, то 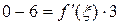 ,
, 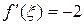 . Точку ξ найдем из уравнения
. Точку ξ найдем из уравнения 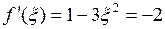 . Отсюда
. Отсюда 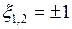 . Искомой является точка
. Искомой является точка 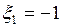 , так как только
, так как только 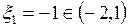 .
.
Следствие из теоремы Лагранжа. Если функция 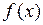 непрерывна на отрезке
непрерывна на отрезке 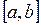 , дифференцируема на интервале
, дифференцируема на интервале 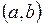 и
и 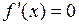 для любых
для любых 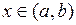 , то
, то 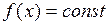 на отрезке
на отрезке 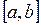 .
.
Этот вывод следует, например, из геометрического смысла производной. Так как касательная к графику функции 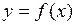 в каждой точке интервала
в каждой точке интервала 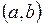 параллельна оси
параллельна оси 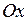
 , то
, то 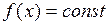 на
на 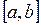 (рис. 4).
(рис. 4).
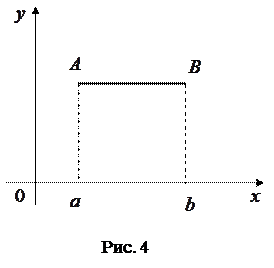 |
Теорема Коши. Пусть функции
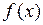 и
и 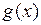 непрерывны на отрезке
непрерывны на отрезке 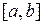 , дифференцируемы на интервале
, дифференцируемы на интервале 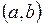 и
и 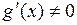 на
на 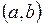 . Тогда существует точка
. Тогда существует точка 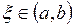 такая, что выполняется равенство
такая, что выполняется равенство
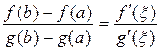 ,
,  . (5)
. (5)
Формулу (5) называют обобщённой формулой конечных приращений или формулой Коши.
Формула Лагранжа (1) является частным случаем формулы Коши при 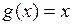 .
.
Пример. Проверить выполнение условий теоремы Коши для функций 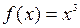 и
и 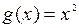 на отрезке
на отрезке 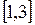 и найти соответствующие значения ξ.
и найти соответствующие значения ξ.
Решение. Очевидно, что функции 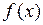 ,
, 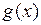 непрерывны на отрезке
непрерывны на отрезке 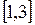 , дифференцируемы на интервале (1, 3), т. к. существуют
, дифференцируемы на интервале (1, 3), т. к. существуют 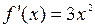 ,
, 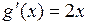 на (1,3). Кроме того,
на (1,3). Кроме того, 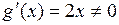 на отрезке (1,3). Таким образом, все условия теоремы Коши выполнены. Следовательно, на интервале (1,3) существует хотя бы одна точка ξ, для которой справедливо равенство
на отрезке (1,3). Таким образом, все условия теоремы Коши выполнены. Следовательно, на интервале (1,3) существует хотя бы одна точка ξ, для которой справедливо равенство 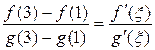 , или
, или 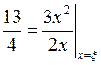 . Отсюда
. Отсюда 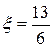 . Полученное значение является искомым, т. к.
. Полученное значение является искомым, т. к. 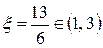 .
.
Date: 2015-09-20; view: 1354; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |