
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Правило Лопиталя. Раскрытие неопределённостей
Теорема 1 (Раскрытие неопределенностей вида 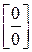 ). Пусть
). Пусть
1) функции f(x) и g(x) определены и дифференцируемы в некоторой окрестности точки a кроме, может быть, самой точки a;
2) 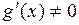 в окрестности точки a;
в окрестности точки a;
3) 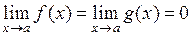 ;
;
4) существует конечный или бесконечный предел отношения производных 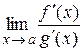 .
.
Тогда существует предел отношения функций 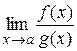 , причем
, причем

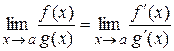 .
.
Пример. Найти 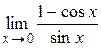 .
.
Решение. Так как 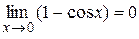 и
и 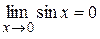 , то имеет место неопределенность вида
, то имеет место неопределенность вида 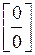 . Функции
. Функции 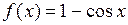 и
и 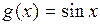 удовлетворяют условиям теоремы 1 в окрестности точки x= 0.
удовлетворяют условиям теоремы 1 в окрестности точки x= 0.
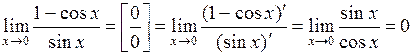 .
.
Замечание. Теорема 1 остаётся справедливой и в случае, когда 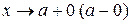 , или когда
, или когда 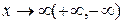 при выполнении условий теоремы в соответствующей полуокрестности точки x = a или в окрестности символа ∞ (+ ∞, - ∞).
при выполнении условий теоремы в соответствующей полуокрестности точки x = a или в окрестности символа ∞ (+ ∞, - ∞).
Пример. Найти  .
.
Решение. Имеем неопределенность вида 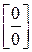 , так как
, так как 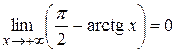 и
и 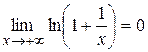 . Функции
. Функции 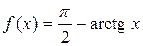 и
и 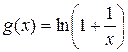 удовлетворяют условиям теоремы 1 в окрестности символа
удовлетворяют условиям теоремы 1 в окрестности символа 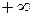 . Следовательно,
. Следовательно,
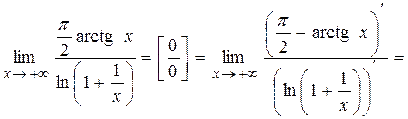
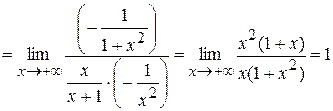 .
.
Теорема 2 (Раскрытие неопределённостей вида 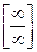 ). Пусть
). Пусть
1) функции f (x) и g (x) определены и дифференцируемы в некоторой окрестности точки a кроме, быть может, самой точки a;
2) 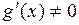 в окрестности точки a;
в окрестности точки a;
3) 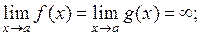
4) существует предел 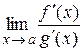 (конечный или бесконечный).
(конечный или бесконечный).
Тогда существует предел 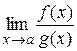 , и
, и 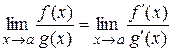 .
.
Замечание. Теорема 2 справедлива и в случае, когда 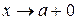
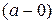 , или когда
, или когда 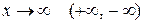 при выполнении условий теоремы в соответствующей полуокрестности точки
при выполнении условий теоремы в соответствующей полуокрестности точки 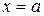 или в окрестности символа ∞ (+ ∞, - ∞).
или в окрестности символа ∞ (+ ∞, - ∞).
Пример. Найти 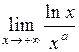 , где a >0.
, где a >0.
Решение. Имеем неопределенность вида 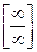 , т. к.
, т. к. 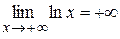 и
и 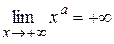 при a > 0. Функции
при a > 0. Функции 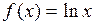 и
и 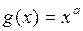 удовлетворяют условиям теоремы 2 в окрестности символа + ∞. Следовательно,
удовлетворяют условиям теоремы 2 в окрестности символа + ∞. Следовательно,
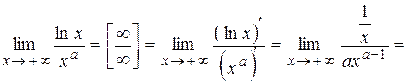
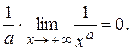
Полученный результат означает, что при 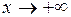 функция
функция 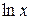 растет медленнее, чем любая степенная функция с положительным показателем.
растет медленнее, чем любая степенная функция с положительным показателем.
Замечания. 1).Правилом Лопиталя (де Гийом Франсуа Лопиталь (1661-1704) - французский математик)называют правило вычисления предела отношения функций по формуле
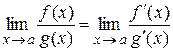 ,
,
если 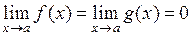 или
или 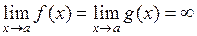 (+ ∞, - ∞) при выполнении всех условий теоремы 1 или теоремы 2 соответственно.
(+ ∞, - ∞) при выполнении всех условий теоремы 1 или теоремы 2 соответственно.
2). Правило Лопиталя можно применять и для нахождения одностороннего предела (при 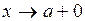 или
или 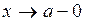 ). В этом случае достаточно потребовать, чтобы функции f (x) и g (x) удовлетворяли условиям теорем 1 и 2 соответственно в правой или левой полуокрестности точки x=a.
). В этом случае достаточно потребовать, чтобы функции f (x) и g (x) удовлетворяли условиям теорем 1 и 2 соответственно в правой или левой полуокрестности точки x=a.
Пример. Найти 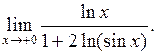
Решение. Имеем неопределенность вида 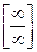 , т. к.
, т. к.  и
и 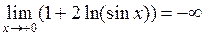 .
.
Функции 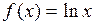 и
и 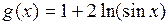 удовлетворяют условиям теоремы 2 в правой полуокрестности нуля.
удовлетворяют условиям теоремы 2 в правой полуокрестности нуля.
Учитывая, что 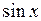 ~
~ 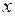 при
при 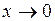 , находим
, находим
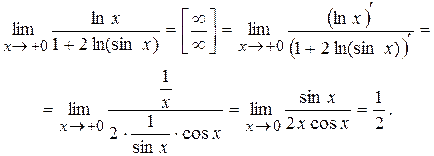
Замечание. Если при 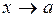 предел отношения производных
предел отношения производных 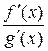 не существует, то правило Лопиталя неприменимо. При этом предел отношения функций
не существует, то правило Лопиталя неприменимо. При этом предел отношения функций 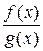 при
при 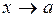 может существовать.
может существовать.
Пример. Найти 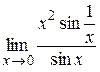 .
.
Решение. Имеем неопределенность вида 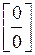 , т. к.
, т. к. 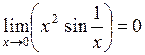 и
и 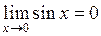 (при вычислении первого предела использована теорема о произведении бесконечно малой функции на ограниченную.)
(при вычислении первого предела использована теорема о произведении бесконечно малой функции на ограниченную.)
В данном случае правило Лопиталя неприменимо, так как предел отношения производных не существует. Действительно, производная числителя 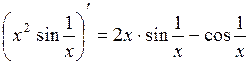 при
при 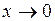 предела не имеет, т.к.
предела не имеет, т.к. 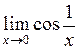 не существует. Однако предел может быть найден, если преобразовать функцию под знаком предела и использовать 1-й замечательный предел:
не существует. Однако предел может быть найден, если преобразовать функцию под знаком предела и использовать 1-й замечательный предел:
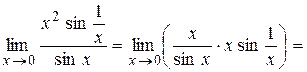
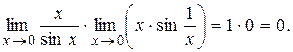
Замечание. Правило Лопиталя можно применять несколько раз, проверяя каждый раз условия теорем 1 или 2.
Пример. Вычислить 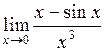 .
.
Решение. Имеем неопределенность вида 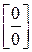 . Применяя правило Лопиталя дважды, получим
. Применяя правило Лопиталя дважды, получим
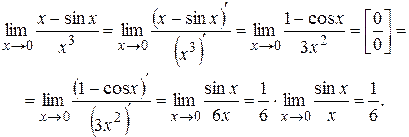
Пример. Вычислить 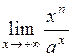 , если
, если 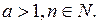
Решение. Имеем неопределенность вида 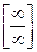 . Применяя правило Лопиталя n раз, найдем
. Применяя правило Лопиталя n раз, найдем
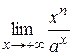 =
= 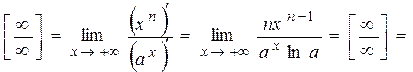
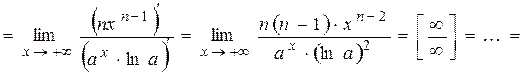
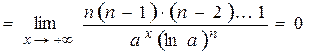 .
.
Получили, что при 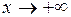 степенная функция с натуральным показателем растет медленнее, чем показательная функция, основание которой больше единицы.
степенная функция с натуральным показателем растет медленнее, чем показательная функция, основание которой больше единицы.
Раскрытие неопределённостей вида 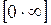 и
и 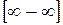
Указанные неопределённости можно свести к неопределённости вида 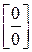 или
или 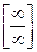 с помощью алгебраических преобразований функции под знаком предела. Действительно, пусть
с помощью алгебраических преобразований функции под знаком предела. Действительно, пусть 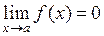 ,
, 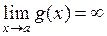 . Тогда
. Тогда
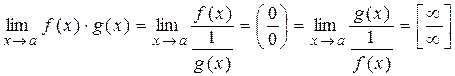 .
.
Если 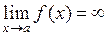 и
и 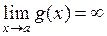 , то
, то 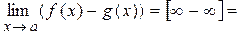
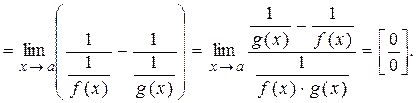
Пример. Вычислить 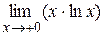 .
.
Решение. Имеем неопределённость вида 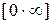 . Записывая произведение функций в виде частного и применяя правило Лопиталя, найдем
. Записывая произведение функций в виде частного и применяя правило Лопиталя, найдем
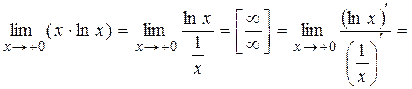
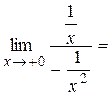
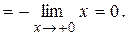
Пример. Вычислить 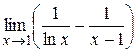 .
.
Решение. Так как 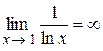 и
и 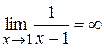 , то имеет место неопределённость вида
, то имеет место неопределённость вида 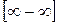 . Преобразовывая выражение под знаком предела и дважды применяя правило Лопиталя, получим
. Преобразовывая выражение под знаком предела и дважды применяя правило Лопиталя, получим
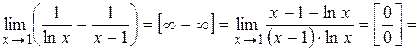
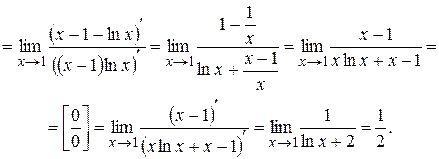
Раскрытие неопределённостей вида [1∞], [∞0], [00]
К данным неопределённостям сводится вычисление пределов показательно-степенной функции 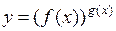 ,
, 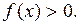 Действительно,
Действительно,
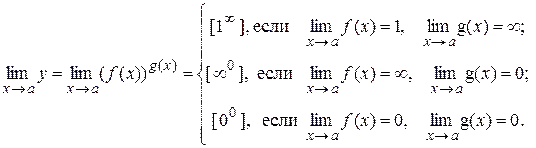
Указанные пределы вычисляются путем перехода к неопределённости вида [ 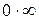 ].
].
Используя основное логарифмическое тождество (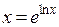
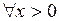 ) для записи функции под знаком предела и непрерывность показательной функции, получим (опуская аргумент у функций f и g),
) для записи функции под знаком предела и непрерывность показательной функции, получим (опуская аргумент у функций f и g),
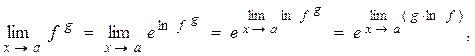 или
или
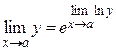 (y > 0). (6)
(y > 0). (6)
Отметим, что для всех рассматриваемых неопределённостей [1∞], [∞0], [00] предел 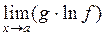 есть неопределённость вида
есть неопределённость вида 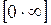 .
.
Пусть найден 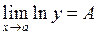 , тогда
, тогда
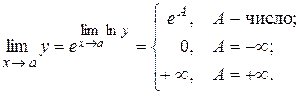
Пример. Найти 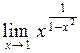 .
.
Решение. Имеем неопределённость вида [1∞],так как 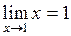 и
и 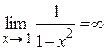 . Полагая
. Полагая 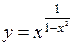 и учитывая формулу (4.6), запишем:
и учитывая формулу (4.6), запишем:
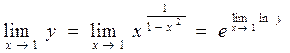 .
.
Вычислим 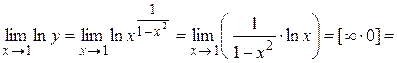
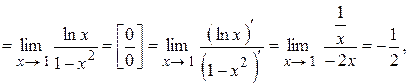 или
или 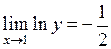 .
.
Следовательно, 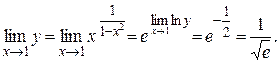
Замечание. Неопределённость вида [1∞] может быть раскрыта с помощью 2-го замечательного предела.
Так, предел 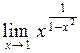 можно вычислить с помощью 2-го замечательного предела следующим образом.
можно вычислить с помощью 2-го замечательного предела следующим образом.
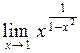 =
= 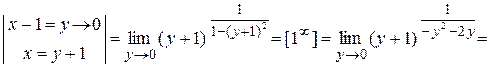
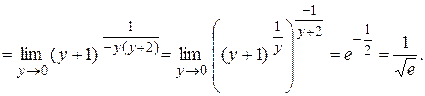
Пример. Найти 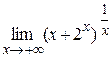 .
.
Решение. Имеем неопределённость вида [∞0], т. к. 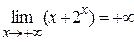 и
и 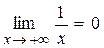 . По формуле (6) запишем:
. По формуле (6) запишем: 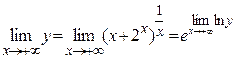 .
.
Вычислим 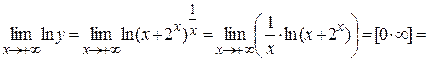
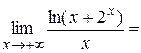
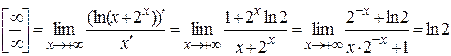 ,
,
учитывая, что 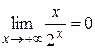 .
.
Следовательно, 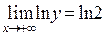 , откуда
, откуда
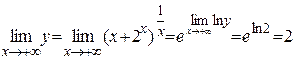 .
.
Контрольные вопросы:
1. Перечислите основные теоремы дифференциального исчисления. Раскройте смысл каждой из них.
2. Как раскрывается неопределенность вида 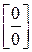 ?
?
3. Как раскрывается неопределенность вида 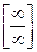 ?
?
4. Как раскрываются неопределенности вида 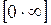 и
и 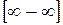 ?
?
5. Как раскрываются неопределенности вида [1∞], [∞0], [00]?
Литература:
1. Высшая математика для экономистов: Учебник для вузов / Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н.Фридман. Под ред. Н.Ш. Кремера. – М.: ЮНИТИ, 2005. – 471 с.
2. Общий курс высшей математики для экономистов: Учебник. / Под ред. В.И. Ермакова. –М.: ИНФРА-М, 2006. – 655 с.
3. Сборник задач по высшей математике для экономистов: Учебное пособие / Под ред.В.И. Ермакова. М.: ИНФРА-М, 2006. – 574 с.
4. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч. 1, 2. – М.: Оникс 21 век: Мир и образование, 2005. – 304 с. Ч. 1; – 416 с. Ч. 2.
5. Математика в экономике: Учебник: В 2-х ч. / А.С. Солодовников, В.А. Бабайцев, А.В. Браилов, И.Г. Шандара. – М.: Финансы и статистика, 2006.
6. Шипачев В.С. Высшая математика: Учебник для студ. вузов – М.: Высшая школа, 2007. – 479 с.
Date: 2015-09-20; view: 1050; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |