
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Пример выполнения задания
Дана схема механизма (рисунок 4).
Расчеты произвести при следующих данных:
m1 =4 кг; m2 =3 кг; m3 =2 кг; m4 =1 кг; 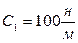 ;
; 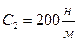 ;
; 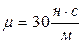 ;
;
Fо =100Н; p =4с-1; R2 =0,2м; R4 =0,1м; ℓ =0,5м; yо =0,2м;  .
.
Механическая система состоит из ведущего груза 1, движение которого передается круглому однородному диску 2, с которым жестко скреплен стержень длиной ℓ. К стержню в точке К присоединены две последовательно соединенные пружины, коэффициенты жесткости которых С1 и С2. Стержень 3 соединен с катком 4 с помощью невесомого стержня АВ. К центру масс катка присоединен невесомый шток демпфера.

Рисунок 4
2.3. Получение дифференциального уравнения движения системы с помощью теоремы о кинетической энергии
Составим расчетную схему задачи (рисунок 5).
Рассматриваемая механическая система имеет одну степень свободы, потому что ее положение однозначно можно определить с помощью координаты у. Начало отсчета координаты совместим с положением статического равновесия центра масс груза 1.
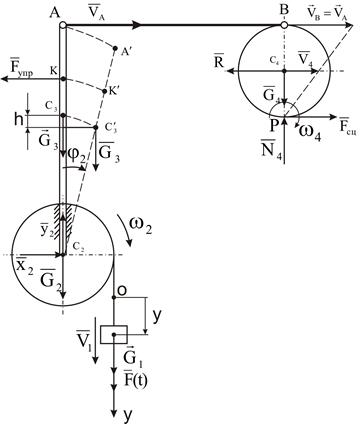
Рисунок 5
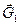 ,
, 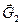 ,
, 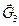 ,
, 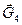 - силы тяжести;
- силы тяжести;
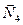 - нормальная реакция опорной плоскости;
- нормальная реакция опорной плоскости;
 - сила сцепления;
- сила сцепления;
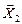 и
и 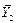 - реакции подшипника диска 2;
- реакции подшипника диска 2;
 - сила вязкого сопротивления;
- сила вязкого сопротивления;
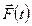 - возмущающая сила.
- возмущающая сила.
Для получения дифференциального уравнения движения системы используем теорему об изменении кинетической энергии системы в дифференциальной форме
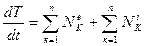 (2.1)
(2.1)
где Т - кинетическая энергия системы;
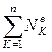 -сумма мощностей внешних сил, действующих на систему;
-сумма мощностей внешних сил, действующих на систему;
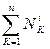 - сумма мощностей внутренних сил.
- сумма мощностей внутренних сил.
Так как тела системы недеформируемы, а шарниры на концах стержня идеальны (без трения), то данная механическая система является неизменяемой. Поэтому сумма мощностей всех внутренних сил системы равна нулю. Следовательно, для данной механической системы теорема (2.1) запишется в виде
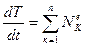 (2.2)
(2.2)
Вычислим кинетическую энергию системы как сумму кинетических энергий тел, входящих в систему
Т = Т1 + Т2 + Т3 + Т4 (2.3)
Кинетическая энергия груза 1, движущегося поступательно со скоростью V 1
 (2.4)
(2.4)
Кинетическая энергия блока 2, вращающегося вокруг неподвижной оси
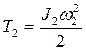 , (2.5)
, (2.5)
где  - момент инерции блока относительно оси, проходящей через его центр масс; ω2 – угловая скорость блока.
- момент инерции блока относительно оси, проходящей через его центр масс; ω2 – угловая скорость блока.
Кинетическая энергия стержня, вращающегося вокруг неподвижной оси
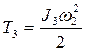 , (2.6)
, (2.6)
где 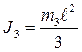 - момент инерции стержня относительно его нижнего торца.
- момент инерции стержня относительно его нижнего торца.
Кинетическая энергия катка, совершающего плоское движение
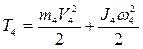 (2.7)
(2.7)
где V4 - скорость центра масс катка 4; ω4 - угловая скорость катка;
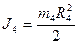 - момент инерции катка относительно его центра масс.
- момент инерции катка относительно его центра масс.
Суммируя кинетические энергии тел системы, получаем
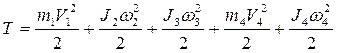 (2.8)
(2.8)
Все скорости входящие в выражение (2.8) можно выразить через скорость V1 ведущего тела. Для этого составим кинематические соотношения
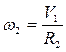 ;
;  ;
; 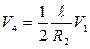 ;
;  (2.9)
(2.9)
Подставляя (2.9) и формулы для моментов инерции тел в (2.8), получаем
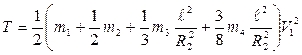 (2.10)
(2.10)
Последнее выражение кинетической энергии системы можно записать в компактной форме, напоминающей кинетическую энергию материальной точки
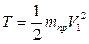 (2.11)
(2.11)
где 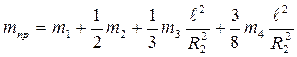 (2.12)
(2.12)
называется приведенной массой.
Поскольку 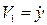 , то окончательное выражение кинетической энергии имеет вид
, то окончательное выражение кинетической энергии имеет вид 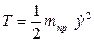 (2.13)
(2.13)
Дифференцируя (2.13) по времени, с учетом, что приведенная масса – величина постоянная, получаем
 (2.14)
(2.14)
Таким образом, левая часть теоремы (2.2) сформирована.
Вычислим теперь сумму мощностей всех внешних сил. Известно, что мощность силы равна 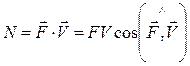 , а мощность момента силы
, а мощность момента силы  .
.
Из последних формул следует, что мощность силы будет равняться нулю, если сила приложена к неподвижной точке. Как видно из расчетной схемы таковыми являются силы  ,
,  ,
, 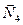 ,
, 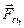 ,
, 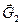 .
.
Мощность силы также равняется нулю, когда сила перпендикулярна вектору скорости. Это будет для силы 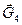 .
.
Вычисляем мощности остальных сил.
Мощность силы тяжести 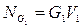
Мощность возмущающей силы 
Мощность силы тяжести G3 вычислим, как мощность момента этой силы относительно точки С2.

Мощность упругой силы Fупр
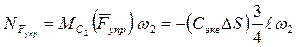
здесь Сэкв – коэффициент жесткости эквивалентной пружины;
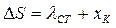 - удлинение эквивалентной пружины;
- удлинение эквивалентной пружины;
λСТ - статическая деформация эквивалентной пружины;
xк - перемещение точки крепления пружины.
Заметим, что если имеются две последовательно соединенные пружины с коэффициентами жесткости С1 и С2, то они заменяются одной эквивалентной пружиной с коэффициентом жесткости 
Если же пружины соединены параллельно, то коэффициент жесткости эквивалентной пружины Сэкв = С1+С2.
В нашем случае 
Мощность силы вязкого сопротивления
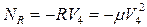
Суммируя приведенные выше мощности внешних сил, с учетом кинематических соотношений (2.9), получаем
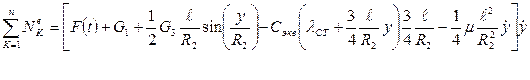
Полученное выражение для суммы мощностей внешних сил можно записать компактно в виде
 (2.15)
(2.15)
где
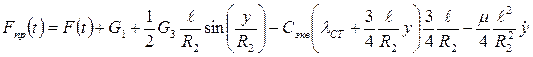 (2.16)
(2.16)
Величину Fпр (t) будем называть приведенной силой.
В этом выражении неизвестной величиной является статическая деформация пружин λСТ,. Имеется также нелинейное слагаемое содержащее множитель  .
.
Поскольку будем изучать линейные колебания системы, при которых переменная у считается величиной первого порядка малости, то приближенно можно положить 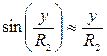
Статическую деформацию λСТ определяем из условия равновесия механической системы. Уравнение равновесия системы можно получить из выражения приведенной силы (2.16), приняв в последнем F(t)=0, y=0;  =0.
=0.
Выполняя эти условия, получаем уравнение равновесия системы
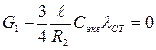 (2.17)
(2.17)
Отсюда, статическая деформация эквивалентной пружины
 (2.18)
(2.18)
Подставляя (2.18) в (2.16), получаем выражение для приведенной силы
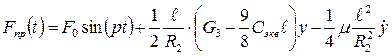 (2.19)
(2.19)
Подставляя в выражение теоремы (2.2) производную от кинетической энергии (2.14) и сумму мощностей (2.15), с учетом (2.19), получаем дифференциальное уравнение движения системы
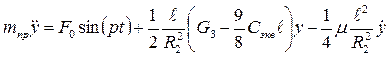 (2.20)
(2.20)
Запишем последнее дифференциальное уравнение в классической форме с общепринятыми коэффициентами, имеющими физический смысл
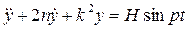 (2.21)
(2.21)
где 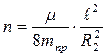 - коэффициент затухания колебаний (2.22)
- коэффициент затухания колебаний (2.22)
Круговая частота свободных колебаний определяется по формуле
 (2.23)
(2.23)
 - относительная амплитуда возмущающей силы (2.24)
- относительная амплитуда возмущающей силы (2.24)
Запишем начальные условия движения:
при t=0, 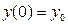 ,
, 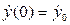 (2.25)
(2.25)
Таким образом, полученное дифференциальное уравнение движения (2.21) совместно с начальными условиями (2.25) представляют собой математическую модель движения рассматриваемой механической системы. По виду дифференциального уравнения (2.21) можно сделать вывод, что механическая система под действием внешних сил совершает линейные вынужденные колебания с учетом сопротивления, возникающего от гашения колебаний демпфером.
2.4. Получение дифференциального уравнения движения системы с помощью принципа Даламбера-Лагранжа
Общее уравнение динамики системы есть математическое выражение принципа Даламбера-Лагранжа.
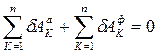 (2.26)
(2.26)
Здесь,
 - сумма элементарных работ всех активных сил на возможном перемещении системы;
- сумма элементарных работ всех активных сил на возможном перемещении системы;
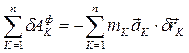 - сумма элементарных работ всех сил инерции на возможном перемещении системы.
- сумма элементарных работ всех сил инерции на возможном перемещении системы.
Изобразим расчетную схему задачи, на которой укажем активные силы и силы инерции (рисунок 6).
Реакции идеальных связей 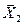 ,
, 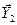 ,
, 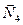 на расчетной схеме не изображаем, потому что сумма элементарных работ всех реакций идеальных связей на любом возможном перемещении системы равна нулю.
на расчетной схеме не изображаем, потому что сумма элементарных работ всех реакций идеальных связей на любом возможном перемещении системы равна нулю.
Укажем на расчетной схеме ускорения, с которыми движутся тела системы и изобразим в соответствии с принципом Даламбера главные векторы и главные моменты сил инерции.
Главные векторы сил инерции и главные моменты сил инерции вычисляются по формулам
Ф1=m1a1; 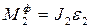 ;
; 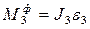 ;
; 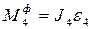 ; Ф4 = m4a4 (2.27)
; Ф4 = m4a4 (2.27)
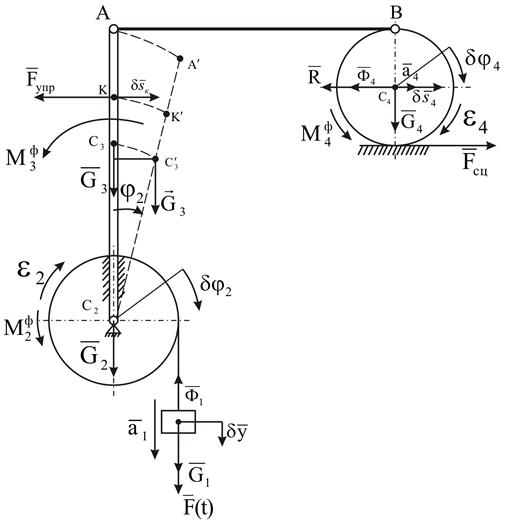
Рисунок 6
Сообщим системе возможное перемещение, допускаемое наложенными на систему связями. Возможную работу активных сил вычисляем как сумму следующих элементарных работ
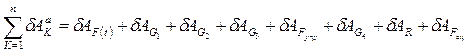 (2.28)
(2.28)
Возможные работы сил тяжести G2 и силы сцепления равны нулю, так как точки приложения сил остаются неподвижными  ;
;  .
.
Возможная работа силы тяжести G4 также равна нулю, так как сила и возможное перемещение ее точки приложения взаимно перпендикулярны
 .
.
Для других активных сил имеем следующие выражения для возможных работ

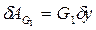
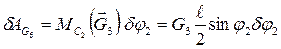 (2.29)
(2.29)
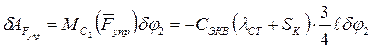

Используя кинематические соотношения (2.9) составим аналогичные соотношения между возможными перемещениями
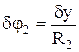 ;
;  ;
;  . (2.30)
. (2.30)
С учетом (2.30) возможную работу активных сил можно записать в виде
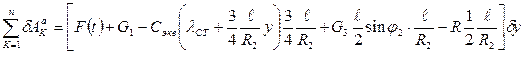
или 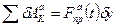 (2.31)
(2.31)
Следовательно, выражение для активной приведенной силы имеет вид
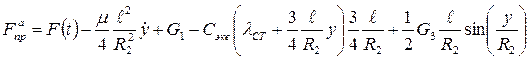 (2.32)
(2.32)
или с учетом малости изучаемых колебаний, полагаем

статическую деформацию λСТ, как и в предыдущем параграфе определяем из условия статического равновесия системы 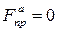 . Полагая в (2.32) F(t)=0,
. Полагая в (2.32) F(t)=0, 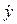 =0; у=0, находим
=0; у=0, находим
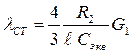 (2.33)
(2.33)
Подставляя λСТ в (2.32) и с учетом малости колебаний, получаем окончательное выражение активной приведенной силы
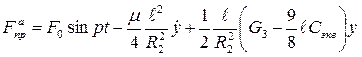 , (2.34)
, (2.34)
которое совпадает с выражением приведенной силы, полученной в предыдущем параграфе (2.19).
Найдем теперь возможную работу сил инерции
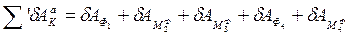 (2.35)
(2.35)
Здесь


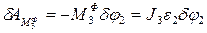 (2.36)
(2.36)
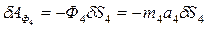

Используя кинематические соотношения для скоростей (2.9), получим аналогичные соотношения для ускорений
 ;
; 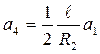 ;
; 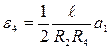 (2.37)
(2.37)
Суммируя возможные работы сил инерции с учетом (2.30) и (2.37), получаем
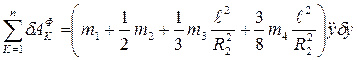 (2.38)
(2.38)
или 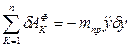 (2.39)
(2.39)
где приведенная масса
 (2.40)
(2.40)
Аналогичное выражение приведенной массы было получено ранее в предыдущем параграфе (2.12)
Подставляя выражение (2.31) и (2.39) в общее уравнение динамики (2.26), получаем
 (2.41)
(2.41)
Поделив в (2.41) на δу≠ 0, получаем
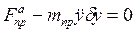 (2.42)
(2.42)
Подставляя в (2.42) выражение приведенной активной силы (2.34) и выполняя преобразования, получаем дифференциальное уравнение движения системы
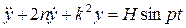 (2.43)
(2.43)
где 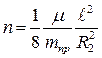
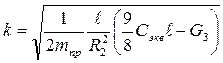
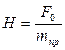 .
.
Дифференциальное уравнение вынужденных колебаний системы (2.43) полностью совпадает с полученным ранее уравнением (2.21).
2.5. Получение дифференциального уравнения движения системы с помощью уравнения Лагранжа II рода
Рассматриваемая механическая система при принятых условиях расчета имеет одну степень свободы. Примем за обобщенную координату системы вертикальное отклонение у груза 1 от положения покоя (рисунок 7), соответствующего статической деформации пружин.
Для механической системы с одной степенью свободы дифференциальное уравнение движения системы в обобщенных координатах имеет вид
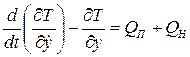 , (2.44)
, (2.44)
где Т - кинетическая энергия системы;
QП - обобщенная потенциальная сила;
QН - обобщенная непотенциальная сила;
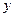 – обобщенная координата;
– обобщенная координата;
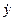 – обобщенная скорость.
– обобщенная скорость.
Выражение для кинетической энергии системы было найдено ранее (2.13).
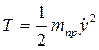
где 
Производные от кинетической энергии
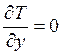 ;
; 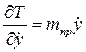 ;
; 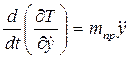 (2.45)
(2.45)
Все внешние силы, действующие на тела системы можно разделить на потенциальные и непотенциальные. К потенциальным силам относятся сила тяжести и упругая сила, к непотенциальным силам относятся возмущающая сила и сила вязкого сопротивления.
Чтобы вычислить потенциальную обобщенную силу Qп надо найти потенциальную энергию системы
 (2.46)
(2.46)
Вычислим потенциальные энергии указанных сил
 ;
;
 ;
;
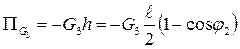 ; (2.47)
; (2.47)
 ;
;

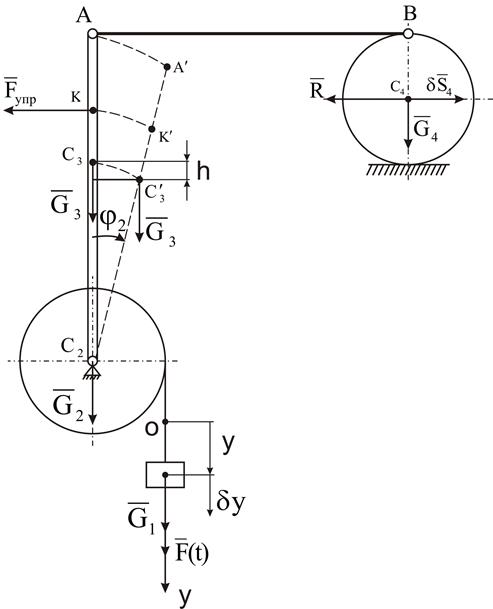
Рисунок 7
Функцию cosφ2 разложим в ряд и удержим в этом ряду первые два слагаемые
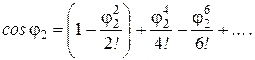
Суммируя потенциальные энергии (2.47) и учитывая, что
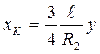 ;
; 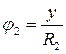 получим
получим
 (2.48)
(2.48)
Статическую деформацию пружины находим из условия равновесия системы
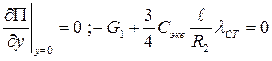
Отсюда 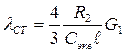 (2.49)
(2.49)
Подставляя статическую деформацию (2.49) в выражение потенциальной энергии (2.48) окончательно получаем
 (2.50)
(2.50)
Тогда обобщенная потенциальная сила
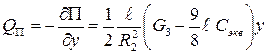 (2.51)
(2.51)
Чтобы определить обобщенную силу непотенциальных сил, вычислим элементарную работу этих сил на возможном перемещении
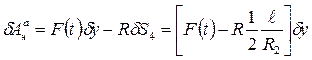 (2.52)
(2.52)
Известно, что возможную работу непотенциальных сил можно записать в виде 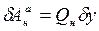 (2.53)
(2.53)
Сравнивая (2.52) и (2.53), получаем выражение непотенциальной обобщенной силы
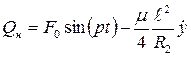 (2.54)
(2.54)
Подставляя (2.45), (2.51), (2.54) в уравнение Лагранжа (2.44), приходим к дифференциальному уравнению движения
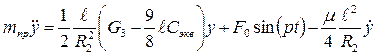
или 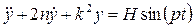 (2.55)
(2.55)
где 
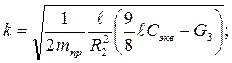
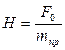
Полученное дифференциальное уравнение (2.55) полностью совпадает с уравнениями движения (2.21) и (2.43), полученными другими способами.
Date: 2015-08-15; view: 480; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |