Глава 3. Специальная версия аналитической формы Теоремы Хана - Банаха

Здесь мы рассматриваем случаи, когда минорируемый линейный функционал может принимать бесконечные значения.

Пусть – векторное пространство над полем вещественных чисел . Далее 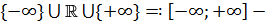расширенная вещественная прямая с естественным отношением порядка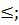 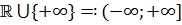и 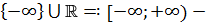полурасширения соответственно вправо и влево.

Для множеств 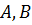через обозначим множество всех отображений 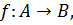или функционалов, если это или одно из расширений , или функций, если 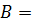. Для 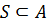сужение 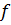на 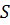обозначим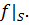

Через 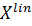обозначим пространство линейных функционалов 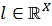на , т.е. 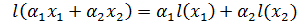для любых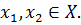

Пусть 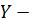векторное подпространство в . Функционал допускает двойственное представление (сверху) на векторе 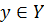относительно 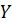, если

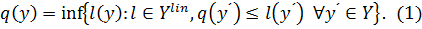
Если (1) выполнено для любог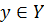о , то 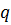допускает двойственное линейное представление на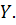

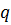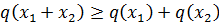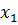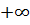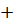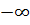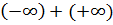Функционал супераддитивный на , если для всех , . Поскольку суммы () () и в [ 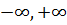] не определены, данное здесь опре­деление супераддитивности корректно только в двух случаях: когда образ

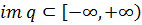или

Функционал 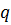положительно однородный, если 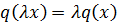для всех 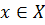и 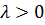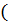при этом 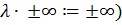. В частности, если 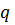- положительно однородный функционал и 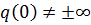, то .

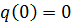Функционал 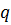вогнутый, если неравенство

выполнено для всех и 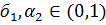, 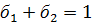. Из тех же соображений, что и при определении супераддитивности, определение вогнутости функционала корректно только в двух случаях (2). Символами 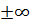обозначаем также и функционалы

,

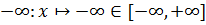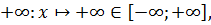
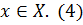
Для пустого подмножества полагаем

При этом справедливо элементарное

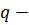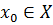Предложение 3.1. Пусть супераддитивный или вогнутый функционал на и существует вектор , для которого . Тогда 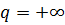в обозначениях (4) и допускает двойственное линейное представление (сверху) на .

Доказательство. Для произвольного вектора 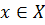при супераддитивности 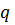имеем

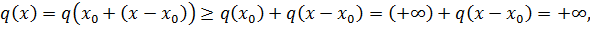
а при вогнутости 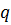получаем

.

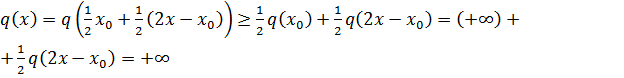В силу (5) для функционала 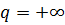при 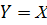получаем, что выполнено

(1)

(а из этого следует, что функционал 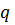допускает двойственное линейное представление (сверху) на векторе 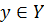относительно 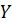(векторного подпространства в 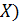) и двойственное линейное представление на .

Теперь в определение вогнутости неравенство (3) можно распространить и на случай 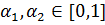, если в 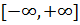полагать

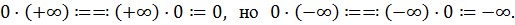
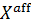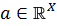Через обозначаем векторное пространство над аффинных функционалов на 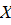, т.е.

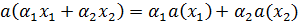
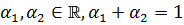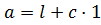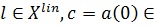
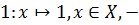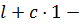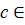
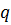для любых , . Каждый такой функционал однозначно представляется в виде , где и функция, равная тождественно 1, и наоборот, каждый функционал вида аффинный. Отметим также, что для любого функционал вогнутый, если и только если 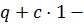вогнутый функционал.

Функционал допускает двойственное аффинное представление (сверху) на векторе 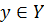относительно подпространства 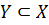, если

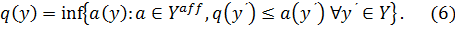
Если (6) выполнено для любог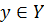о , то 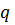допускает двойственное аффинное представление на .

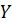Пусть 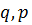- функционалы, определенные на некотором множестве 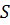, со значениями в 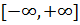. Пишем 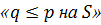, если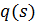 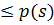для всех 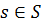. Другими словами, 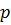мажоририет 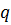на S, или 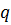миноририет на S.

Date: 2015-07-02; view: 346; Нарушение авторских прав