Глава 1.Основные сведения, понятия и определения

Определение 1.1. Линейным (векторным) пространством называется множество 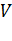произвольных элементов, называемых векторами, в котором определены операции сложения векторов и умножения вектора на число, т.е. любым двум векторам 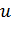и 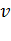поставлен в соответствие вектор 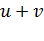, называемый суммой векторов 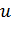и 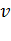, любому вектору 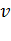и любому числу 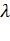из поля действительных чисел поставлен в соответствие вектор 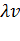, называемый произведением вектора 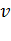на число 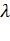и при этом выполняются следующие аксиомы линейного пространства:

1. 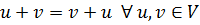(коммутативность сложения);

2. 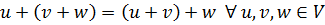(ассоциативность сложения);

3. Существует такой элемент 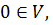называемый нулевым вектором, что ;

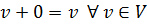4. Для каждого вектора 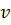существует такой вектор 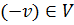, называемый противоположным вектору 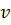, что ;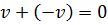

5. ;

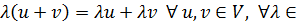
6. ;

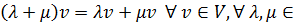
7.

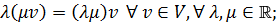
8. .

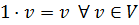Условия 1-8 называются аксиомами линейного пространства. Знак равенства, поставленный между векторами, означает, что в левой и правой частях равенства представлен один и тот же элемент множества 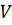. Такие векторы называются равными.

В определении линейного пространства операция умножения вектора на число введена для действительных чисел. Такое пространство называют линейным пространством над полем действительных (вещественных) чисел, или, короче, вещественным линейным пространством. Если в определении вместо поля действительных чисел взять поле комплексных чисел , то получим линейное пространство над полем комплексных чисел, или, короче, комплексное линейное пространство. В качестве числового поля можно выбрать и поле рациональных чисел, при этом получим линейное пространство над полем рациональных чисел.

Определение 1.2.Непустое подмножество 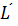линейного пространства 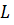называется подпространством, если оно само образует линейное пространство по отношению к определенным в 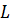операциям сложения и умножения на число.

Иначе говоря, есть подпространство, если из следует, что 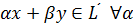и .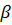

Во всяком линейном пространстве 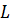имеется подпространство, состоящее из одного нуля – нулевое подпространство. С другой стороны, все 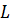можно рассматривать как свое подпространство. Подпространство, отличное от 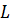и содержащее хотя бы один ненулевой элемент называется собственным.

Определение 1.3.Линейные функционалы. Числовую функцию 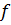, определенную на некотором векторном пространстве 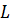,будем называть функционалом. Функционал 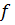называется аддитивным, если

он называется однородным, если

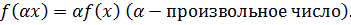
Функционал 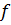, определенный в комплексном линейном пространстве называется сопряженно-однородным, если 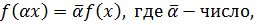комплексно сопряженное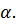

Аддитивный однородный функционал называется линейным функционалом. Аддитивный сопряжено-однородный функционал называется сопряжено линейным, а иногда полулинейным.

Пусть - линейное множество. Отображение 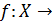называется линейным функционалом, если

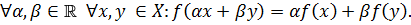
Определение 1.4.Линейное пространство называется нормированным, если любому элементу 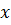поставлено в соответствие число, называемое нормой, и обозначаемое 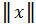и при этом выполнены следующие условия:

1.

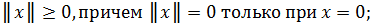
2.

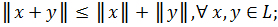
3.

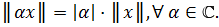
Определение 1.5.Пусть линейное пространство. Линейный функционал 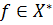непрерывен в точке 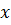, если .

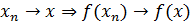Определение 1.6.Пусть 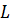– некоторое линейное действительное пространство и 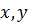– две его точки. Назовем замкнутым отрезком в 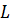, соединяющим точки 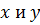, совокупность всех элементов вида

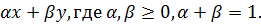
Отрезок без концевых точек 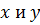называется открытым отрезком.

Множество 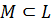называется выпуклым, если оно вместе с любыми двумя точками 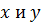содержит и соединяющий их отрезок.

Определение 1.7.Пусть 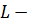действительное линейное пространство. Определенный на 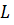функционал 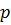называется выпуклым если

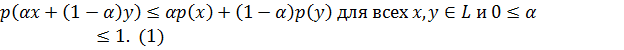
Функционал 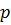называется положительно-однородным если

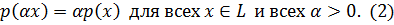
Для выпуклого положительно-однородного функционала выполнено неравенство:

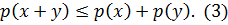
Действительно

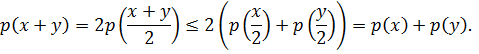
Условие (2) и условие (3) обеспечивают выпуклость функционала 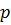. Положительно-однородный выпуклый функционал называют еще однородно-выпуклым.

Всякий линейный функционал является однородно-выпуклым.

Некоторые свойства однородно – выпуклых функционалов:

1. Полагая в равенстве (2), получаем

2. Из (3) и (4) следует, что

3. При любом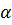

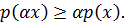
Определение 1.7.Функция 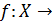называется сублинейным функционалом, если

1. ;

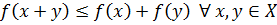2. .

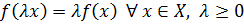Date: 2015-07-02; view: 379; Нарушение авторских прав