Теорема Шеннона для канала без помех

Рассмотрим две фундаментальные теоремы идеального кодирования, носящие имя Шеннона. Первая из них рассматривает случай отсутствия помех в канале, вторая учитывает наличие помех, приводящих к ошибкам.

Рассмотрим проблему согласования источника сообщений и канала при передаче последовательности сообщений. Пусть источник сообщений выдает сообщения с некоторой скоростью 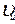(сообщений/ед. времени), называемой технической производительностью источника. Пусть по каналу можно передавать без искажений сообщения со скоростью, не превышающей некоторую величину 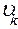(сообщений/ед. времени), называемую технической пропускной способностью канала. Очевидно, что если выполняется условие 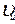< 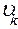, то канал успевает передать все сообщения, поступающие на его вход от источника, и передача будет вестись без искажений. Что произойдет, если 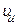> 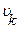? Можно ли в этом случае обеспечить передачу без искажений? Если исходить только из технических характеристик, то, очевидно, нельзя. А если учесть информационные характеристики? Ведь нам известно, что если последовательность обладает информационной избыточностью, то её можно сжать, применив методы экономного кодирования. Рассмотрим подробнее такую возможность.

Пусть V_u - (информационная) производительность источника, т.е. количество информации, производимое источником в единицу времени; C_k – (информационная) пропускная способность канала, т.е. максимальное количество информации, которое способен передать канал без искажений за единицу времени. Первая теорема Шеннона утверждает, что безошибочная передача сообщений определяется соотношением V_u и C_k.

Первая теорема Шеннона: если пропускная способность канала без помех превышает производительность источника сообщений, т.е. удовлетворяется условие C_k >V_u,

то существует способ кодирования и декодирования сообщений источника, обеспечивающий сколь угодно высокую надежность передачи сообщений. В противном случае, т.е. если C_k <V_u

Такого способа нет.

Таким образом, идеальное кодирование по Шеннону по существу представляет собой экономное кодирование последовательности сообщений при безграничном укрупнении сообщений. Такой способ кодирования характеризуется задержкой сообщений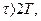

поскольку кодирование очередной типичной последовательности может начаться только после получения последовательности источника длительностью T, а декодирование – только когда принята последовательность из канала той же длительности T. Поскольку требуется 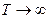, то идеальное кодирование требует бесконечной задержки передачи информации. В этом причина технической нереализуемости идеального кодирования по Шеннону. Тем не менее, значение этого результата, устанавливающего предельные соотношения информационных характеристик источника и канала для безошибочной передачи сообщений, весьма велико. Исторически именно теорема Шеннона инициировала и определила развитие практических методов экономного кодирования.

1. Теорема Шеннона для канала с помехами

При отсутствии помех ошибки при передаче могут возникать только за счет неоднозначного кодирования сообщений. Рассмотрим теперь ситуацию, когда в канале действуют помехи, вызывающие искажения передаваемых символов. Возникающие при этом ошибки носят случайный характер, они действуют при любой скорости передачи сообщений через канал, в том числе, когда V_u<V_k.

Возникает вопрос, возможен ли такой способ кодирования, при котором сообщения передаются через канал без ошибок с некоторой ненулевой скоростью V_{k. 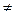0} (действие ошибок полностью устраняется при кодировании)? В первой главе рассматривались методы помехоустойчивости кодирования, основанные на введении избыточности. Однако для полного устранения ошибок их применение потребовало бы введения бесконечной избыточности, что привело бы к снижению скорости передачи сообщений до нуля.

Тем не менее вторая теорема Шеннона утверждает, что такой способ возможен. Тогда возникает следующий вопрос: чем определяется максимальная скорость передачи сообщений по каналу с помехами? Оказывается, что, как и для канала без помех, она определяется соотношением информационных характеристик источника и канала.

Вторая теорема Шеннона: для канала с помехами существует такой способ кодирования, при котором обеспечивается безошибочная передача всех сообщений источника, если только пропускная способность канала превышает производительность источника, т.е. C_k>V_u.

Возникающая ситуация поясняется на рис. 19. На вход канала поступают типичные последовательности источника А_Т. Они кодируются последовательностями канала 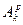, причем для этой цели используется только часть возможных последовательностей канала А_к. Под действием помех входные последовательности изменяются и переходят в выходные последовательности канала В_к, вообще говоря, не совпадающие с переданными.

Получив одну из последовательностей В_к на выходе канала, мы должны принять решение относительно переданной последовательности. Как это сделать? Разобьем множество В_к на непересекающиеся подмножества S_k так, чтобы каждой переданной последовательности соответствовало своё подмножество S_k.. При этом выберем подмножества так, чтобы для каждой вход-

		ной последовательности вероятность попадания в своё подмножество была больше, чем в остальные. Принимая последовательность на выходе, смотрим, к какому подмножеству она относится, и в соответствии с этим принимаем решение о переданной типичной последовательности. Очевидно, что при этом велика вероятность правильно определить переданную последовательность, однако, возможны и ошибки. Ошибка возникает, если входная последовательность перейдет в несоответствующее ей множество Sk (на рис. 19 показан этот случай). Передача будет всегда безошибочной, если удастся так выбрать входные последовательности канала

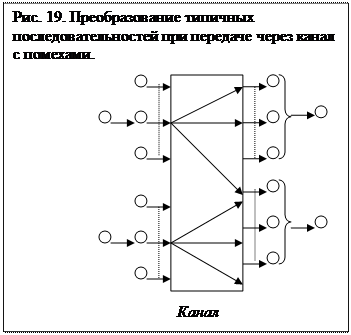и разбиение S_k, что переходы в несоответствующие подмножества будут невозможны или, по крайней мере, будут иметь сколь угодно малую вероятность для больших Т. Возможна ли такая ситуация? Оказывается возможна.

Теорема Шеннона для канала с помехами не указывает конкретного способа кодирования, обеспечивающего достоверную передачу информации со скоростью сколь угодно близкой к пропускной способности канала, а лишь указывает на принципиальное существование такого способа. Кроме того, как и в первой теореме, кодирование будет сопровождаться задержкой сообщений не менее 2Т, где 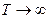. Поэтому идеальное кодирование технически нереализуемо. Однако из формулы для вероятности ошибки вытекает крайне важный практический вывод: достоверность передачи сообщений тем выше, чем больше длительность кодируемой последовательности и чем менее эффективно используется пропускная способность канала, т.е. чем больше запас Ck-Vu.

Теорема Шеннона для канала с помехами оказала огромное влияние на становление правильных взглядов на возможности передачи сообщений и на разработку технически реализуемых методов помехоустойчивого кодирования. Шеннон показал, что для безошибочной передачи сообщений вовсе не обязательно вводить бесконечную избыточность и уменьшать скорость передачи информации до нуля. Достаточно ввести в сообщения источника такую избыточность, которая равна потерям количества информации в канале из-за действия помех.

Date: 2015-07-02; view: 5045; Нарушение авторских прав