
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Теоретические сведения. Цель работы: изучение явлений, наблюдаемых при внешнем возбуждении колебаний с частотами, близкими к резонансной частоте; исследование зависимости тока в
Лабораторная работа № 5
ИССЛЕДОВАНИЕ ВЫНУЖДЕННЫХ КОЛЕБАНИЙ
В 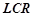 - КОНТУРЕ
- КОНТУРЕ
Цель работы: изучение явлений, наблюдаемых при внешнем возбуждении колебаний с частотами, близкими к резонансной частоте; исследование зависимости тока в контуре, напряжения на конденсаторе и напряжения на катушке индуктивности от частоты вынужденных колебаний в цепях переменного тока; определение добротности контура и индуктивности катушки резонансным методом.
Приборы и принадлежности: генератор напряжений специальной формы (ГСФ), катушка индуктивности Lx, конденсатор емкостью 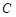 , резистор сопротивлением
, резистор сопротивлением 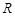 , мультиметр портативный, цифровые вольтметры.
, мультиметр портативный, цифровые вольтметры.
Теоретические сведения
Рассмотрим замкнутую электрическую цепь (контур), состоящую из последовательно соединённых конденсатора ёмкостью 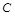 , катушки с индуктивностью
, катушки с индуктивностью 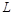 , резистора с активным сопротивлением
, резистора с активным сопротивлением 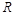 и генератора переменной ЭДС
и генератора переменной ЭДС 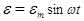 (или напряжения
(или напряжения 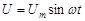 ), где
), где 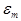 и
и 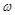 – амплитуда и частота ЭДС (напряжения), вырабатываемого генератором (рис. 5.1).
– амплитуда и частота ЭДС (напряжения), вырабатываемого генератором (рис. 5.1).
 Рис. 5.1. Цепь переменного тока
Рис. 5.1. Цепь переменного тока
| Колебания, возникающие под действием внешней периодически изменяющейся ЭДС, называются вынужденными электромагнитными колебаниями. Электромагнитные возмущения распространяются |
в пространстве и различных устройствах со скоростью света 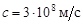 . Расстояние
. Расстояние 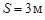 электромагнитное возмущение пробегает за время
электромагнитное возмущение пробегает за время 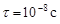 . Поэтому мгновенные значения силы тока во всех точках однородного участка цепи практически одинаковы. Такие токи называют квазистационарными. Мгновенные значения квазистационарных токов подчиняются закону Ома и правилам Кирхгофа. Одно из правил Кирхгофа утверждает, что алгебраическая сумма падений напряжения в замкнутой электрической цепи (контуре) равна алгебраической сумме ЭДС, действующей в цепи.
. Поэтому мгновенные значения силы тока во всех точках однородного участка цепи практически одинаковы. Такие токи называют квазистационарными. Мгновенные значения квазистационарных токов подчиняются закону Ома и правилам Кирхгофа. Одно из правил Кирхгофа утверждает, что алгебраическая сумма падений напряжения в замкнутой электрической цепи (контуре) равна алгебраической сумме ЭДС, действующей в цепи.
Для рассматриваемого контура согласно второму правилу Кирхгофа справедливо уравнение
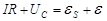 , (5.1)
, (5.1)
где 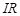 – падение напряжения на резисторе;
– падение напряжения на резисторе; 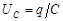 – напряжение на конденсаторе;
– напряжение на конденсаторе; 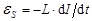 – ЭДС самоиндукции в катушке. Дифференцируя это уравнение по времени и используя соотношение
– ЭДС самоиндукции в катушке. Дифференцируя это уравнение по времени и используя соотношение 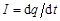 , получим дифференциальное уравнение вынужденных колебаний тока в цепи
, получим дифференциальное уравнение вынужденных колебаний тока в цепи
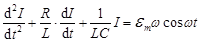 . (5.2)
. (5.2)
Из теории вынужденных колебаний известно, что такое уравнение в случае установившихся колебаний имеет решение
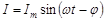 , (5.3)
, (5.3)
где 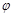 – сдвиг фаз между ЭДС генератора и током.
– сдвиг фаз между ЭДС генератора и током.
Напряжение на резисторе 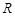 равно
равно
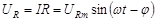 , (5.4)
, (5.4)
где 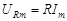 – амплитуда напряжения на резисторе.
– амплитуда напряжения на резисторе.
Сравнение выражений (5.3) и (5.4) приводит к выводу, что сдвиг фаз между 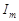 и
и 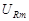 равен нулю.
равен нулю.
Напряжение на конденсаторе определяется формулой
 , (5.5)
, (5.5)
где 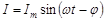 .
.
После подстановки выражения (5.3) в формулу (5.5) и интегрирования 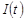 по
по 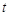 получим
получим
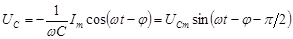 , (5.6)
, (5.6)
где 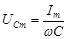 – амплитудное значение напряжения на конденсаторе
– амплитудное значение напряжения на конденсаторе 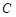 .
.
Из выражений (5.3) и (5.6) видно, что напряжение на конденсаторе отстаёт по фазе от тока на 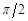 .
.
Напряжение на катушке индуктивности можно найти, применяя закон Ома для участка цепи:
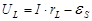 , (5.7)
, (5.7)
где 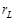 – активное сопротивление катушки, которое в данном случае считается равным нулю, а
– активное сопротивление катушки, которое в данном случае считается равным нулю, а 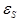 – ЭДС самоиндукции в катушке, которая определяется по формуле
– ЭДС самоиндукции в катушке, которая определяется по формуле
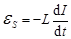 (5.8)
(5.8)
Подставляя выражения (5.3) и (5.8) в уравнение (5.7), получаем
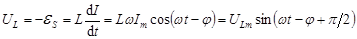 , (5.9)
, (5.9)
где 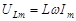 – амплитудное значение напряжения. Из выражений (5.3) и (5.9) видно, что напряжение на катушке опережает по фазе ток на
– амплитудное значение напряжения. Из выражений (5.3) и (5.9) видно, что напряжение на катушке опережает по фазе ток на 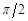 .
.
Соотношения между токами и напряжениями удобно изображать на векторной диаграмме (рис. 5.2). Для этого примем произвольное направление за ось токов. Амплитуду напряжения на резисторе 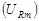 изобразим вектором, направленным вдоль оси токов. Амплитуду напряжения на катушке
изобразим вектором, направленным вдоль оси токов. Амплитуду напряжения на катушке 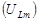 изобразим вектором, повернутым относительно оси тока на угол
изобразим вектором, повернутым относительно оси тока на угол 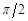 . Аналогично амплитуду напряжения на конденсаторе
. Аналогично амплитуду напряжения на конденсаторе 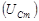 изобразим вектором, повернутым относительно оси токов на угол
изобразим вектором, повернутым относительно оси токов на угол 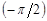 .
.
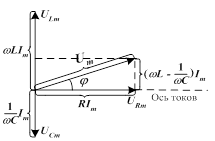 Рис. 5.2. Векторная диаграмма амплитуд напряжений
на резисторе
Рис. 5.2. Векторная диаграмма амплитуд напряжений
на резисторе 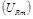 , катушке , катушке 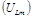 и конденсаторе
и конденсаторе 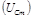
| Падения напряжений 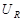 , , 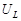 и и 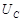 в сумме должны быть равны приложенному к цепи напряжению в сумме должны быть равны приложенному к цепи напряжению 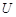 . Сложив векторы, изображающие . Сложив векторы, изображающие 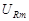 , , 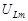 и и 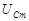 , мы получим вектор, изображающий напряжение , мы получим вектор, изображающий напряжение 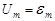 . Этот вектор образует с осью токов угол . Этот вектор образует с осью токов угол 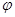 , дающий разность фаз между напряжением , дающий разность фаз между напряжением 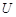 (или ЭДС генератора) и силой тока (или ЭДС генератора) и силой тока 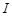 . .
|
По векторной диаграмме находим
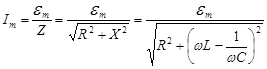 , (5.10)
, (5.10)
Формулу (5.10) называют законом Ома для переменного тока. Величины 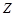 ,
, 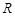 и
и 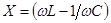 называются соответственно полным,активным и реактивным сопротивлениями цепи для переменного тока, где
называются соответственно полным,активным и реактивным сопротивлениями цепи для переменного тока, где 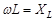 – реактивное индуктивное сопротивление;
– реактивное индуктивное сопротивление; 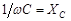 – реактивное емкостное сопротивление;
– реактивное емкостное сопротивление; 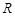 – омическое сопротивление (активное), обуславливающее выделение количества теплоты в цепи в соответствии с законом Джоуля - Ленца. Все эти величины измеряются в Ом.
– омическое сопротивление (активное), обуславливающее выделение количества теплоты в цепи в соответствии с законом Джоуля - Ленца. Все эти величины измеряются в Ом.
Сдвиг фаз 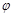 между внешней ЭДС и током определяется соотношением
между внешней ЭДС и током определяется соотношением
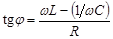 . (5.11)
. (5.11)
Как следует из формул (5.10) и (5.11), обе эти величины – амплитуда тока и фазовый сдвиг – зависят от частоты колебаний 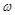 . Если
. Если 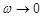 , то
, то 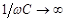 . Тогда сопротивление
. Тогда сопротивление 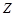 обращается в бесконечность, а амплитуда тока
обращается в бесконечность, а амплитуда тока 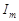 становится равной нулю. При увеличении
становится равной нулю. При увеличении 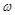 реактивное
реактивное 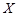 и полное
и полное 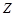 сопротивления сначала уменьшаются, а амплитуда тока
сопротивления сначала уменьшаются, а амплитуда тока 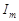 увеличивается. При частоте
увеличивается. При частоте 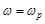 , называемой резонансной и определяемой условием
, называемой резонансной и определяемой условием
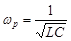 , (5.12)
, (5.12)
реактивное сопротивление 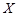 обращается в нуль, полное сопротивление цепи становится наименьшим:
обращается в нуль, полное сопротивление цепи становится наименьшим: 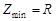 , а амплитуда тока – максимальной:
, а амплитуда тока – максимальной:
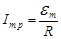 . (5.13)
. (5.13)
Таким образом, при достижении генератором ЭДС частоты 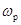 амплитуда тока достигает максимального значения
амплитуда тока достигает максимального значения 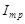 , а сдвиг фаз между током и напряжением равен нулю. Этот важный случай вынужденных колебаний называется резонансом.
, а сдвиг фаз между током и напряжением равен нулю. Этот важный случай вынужденных колебаний называется резонансом.
При значениях 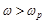 реактивное сопротивление
реактивное сопротивление 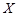 вновь отлично от нуля и с возрастанием
вновь отлично от нуля и с возрастанием 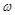 увеличивается. В соответствии с этим полное сопротивление
увеличивается. В соответствии с этим полное сопротивление 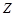 цепи увеличивается, а амплитуда тока
цепи увеличивается, а амплитуда тока 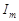 уменьшается, асимптотически приближаясь к нулю.
уменьшается, асимптотически приближаясь к нулю.
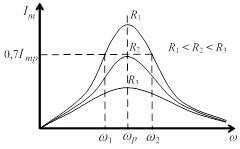 Рис. 5.3. Резонансные кривые
Рис. 5.3. Резонансные кривые
| Графики зависимости амплитуды тока 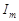 от от 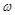 для различных активных сопротивлений контура для различных активных сопротивлений контура 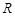 приведены на рис. 5.3. Чем меньше приведены на рис. 5.3. Чем меньше 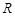 , тем больше при прочих равных условиях амплитуда тока и тем острее максимумы резонансных кривых. , тем больше при прочих равных условиях амплитуда тока и тем острее максимумы резонансных кривых.
|
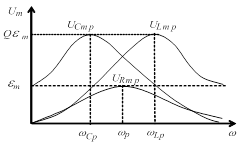 Рис. 5.4. Графики зависимости амплитуды
напряжения на конденсаторе, резисторе и
на катушке индуктивности от частоты
Рис. 5.4. Графики зависимости амплитуды
напряжения на конденсаторе, резисторе и
на катушке индуктивности от частоты
| Резонансная кривая для амплитуды напряжения на резисторе отличается от резонансной кривой для амплитуды тока в нём лишь множителем R (см. формулу (5.4)), то есть максимальное значение 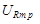 достигается при частоте достигается при частоте 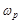 (рис. 5.4).
С изменением частоты (рис. 5.4).
С изменением частоты
|
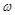 внешней ЭДС изменяется напряжение на конденсаторе
внешней ЭДС изменяется напряжение на конденсаторе 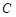 и на катушке индуктивности
и на катушке индуктивности 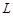 . Графики зависимости
. Графики зависимости 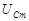 и
и 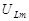 от частоты приведены рис. 5.4. Максимальное значение амплитуды напряжения
от частоты приведены рис. 5.4. Максимальное значение амплитуды напряжения 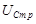 на конденсаторе достигается при частоте
на конденсаторе достигается при частоте
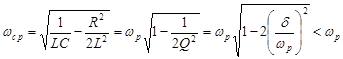 , (5.14)
, (5.14)
где 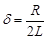 – коэффициент затухания.
– коэффициент затухания.
Максимальное значение амплитуды напряжения 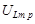 на катушке индуктивности достигается при частоте
на катушке индуктивности достигается при частоте
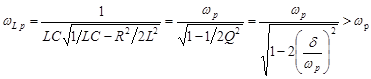 . (5.15)
. (5.15)
Из формул (5.6), (5.9) и (5.13) получаем резонансные значения 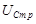 и
и 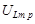 :
:
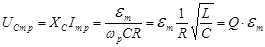 ; (5.16)
; (5.16)
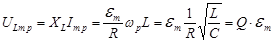 . (5.17)
. (5.17)
Величину
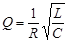 (5.18)
(5.18)
называют добротностью контура. Её значение всегда больше единицы, следовательно, амплитуды этих напряжений превышают амплитудное значение внешней ЭДС 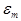 в
в 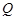 раз (рис. 5.4). Поэтому явление резонанса в последовательном контуре называют резонансом напряжений.
раз (рис. 5.4). Поэтому явление резонанса в последовательном контуре называют резонансом напряжений.
Таким образом, при резонансе амплитудные значения напряжения на конденсаторе 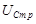 и катушке индуктивности
и катушке индуктивности 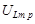 должны быть равны. Как следует из вышеизложенного, сдвиг фаз между этими напряжениями равен
должны быть равны. Как следует из вышеизложенного, сдвиг фаз между этими напряжениями равен 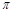 , значит, их сумма равна нулю и в контуре остаются только колебания напряжения на резисторе с амплитудой
, значит, их сумма равна нулю и в контуре остаются только колебания напряжения на резисторе с амплитудой 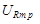 .
.
Важнейшая характеристика резонансных свойств системы – добротность контура 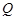 – характеризует остроту резонансных кривых. Чтобы убедиться в этом, вычислим так называемую ширину резонансной кривой для силы тока по половине мощности. Под этой величиной понимают разность частот
– характеризует остроту резонансных кривых. Чтобы убедиться в этом, вычислим так называемую ширину резонансной кривой для силы тока по половине мощности. Под этой величиной понимают разность частот 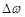 (или
(или 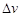 ), для которой
), для которой 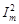 составляет 0,5 от
составляет 0,5 от 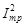 . На рис. 5.3
. На рис. 5.3 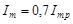 .
.
При резонансе  ,
, 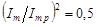 при
при 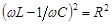 .
.
Это уравнение имеет два корня 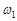 и
и 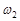 (см. рис. 5.3.). Проведя необходимые выкладки, можно убедиться, что при больших добротностях
(см. рис. 5.3.). Проведя необходимые выкладки, можно убедиться, что при больших добротностях
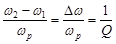 . (5.19)
. (5.19)
Соотношение (5.19) дает возможность экспериментального определения добротности 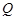 по резонансной кривой силы тока в контуре.
по резонансной кривой силы тока в контуре.
Date: 2015-07-01; view: 404; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |