Метод моментов для точечной оценки параметров распределения

Можно доказать, что начальные и центральные эмпирические моменты являются состоятельными оценками соответственно начальных и центральных теоретических параметров того же порядка. На этом основан метод моментов, предложенный К.Пирсоном. Достоинство метода – сравнительная его простота. Метод моментов точечной оценки неизвестных параметров заданного распределения состоит в приравнивании теоретических моментов рассматриваемого распределения соответствующим эмпирическим моментам того же порядка.

А. Оценка одного параметра. Пусть задан вид плотности распределения f(x, 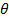), определяемый одним неизвестным параметром 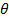. Требуется найти точечную оценку параметра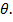

Для оценки одного параметра достаточно иметь одно уравнение относительно этого параметра. Следуя методу моментов, приравняем, например, начальный теоретический момент первого порядка начальному эмпирическому моменту первого порядка: .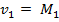

Учитывая, что = 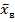, получим

, (*)

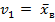Математическое ожидание М(Х), как видно из соотношения

М(Х) = = ,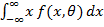

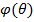есть функция от 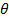, поэтому (*) можно рассматривать как уравнение с одним неизвестным 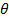. Решив это уравнение относительно параметра 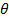, тем самым найдем его точечную оценку 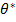, которая является функцией от выборочной средней, следовательно, и от вариант выборки:

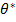= ψ (, , …, .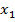

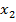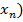Б. Оценка двух параметров. Пусть задан вид плотности распределения 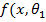, 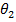), определяемый неизвестными параметрам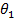и и 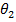. Для отыскания двух параметров необходимы два уравнения относительно этих параметров. Следуя методу моментов, приравняем, например, начальный теоретический момент первого порядка начальному эмпирическому моменту первого порядка и центральный теоретический момент второго порядка центральному эмпирическому моменту второго порядка:

, = .

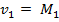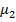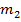Учитывая, что = 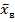, 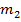= 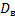, 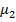= 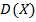, получим

,

= .

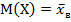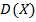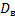Математическое ожидание и дисперсия есть функция от 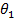и 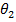, поэтому (**) можно рассматривать как систему двух уравнений с двумя неизвестным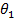и и 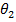. Решив эту систему относительно неизвестных параметров, тем самым получим их точечные оценк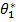и и 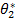. Эти оценки являются функциями от вариант выборки:

= (, , …, ,

= (, , …, .

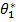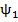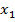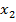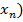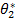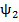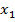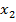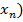Date: 2015-07-17; view: 1073; Нарушение авторских прав