
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Модель Шумана
Модель Шуманаоснована на следующих допущениях:
· общее число команд в программе на машинном языке постоянно;
· в начале компоновочных испытаний число ошибок равно некоторой постоянной величине, и по мере исправления ошибок их становится меньше. В ходе испытаний программы новые ошибки не вносятся;
· ошибки изначально различимы, по суммарному числу исправленных ошибок можно судить об оставшихся;
· интенсивность отказов программы пропорциональна числу остаточных ошибок.
Предполагается, что до начала тестирования (т.е. в момент t=0) имеется M ошибок. В течение времени тестирования τ обнаруживается ε1(t) ошибок в расчете на одну команду в машинном языке.
Тогда удельное число ошибок на одну машинную команду, оставшихся в системе после времени тестирования τ, равно:
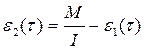 (20)
(20)
где I - общее число машинных команд, которое предполагается постоянным в рамках этапа тестирования.
Предполагается, что значение функции количества ошибок Z(t) пропорционально числу ошибок, оставшихся в программе после израсходованного на тестирование времени τ.
Z (t) = C * ε2 (τ), (21)
где С - некоторая постоянная, t - время работы программы без отказов.
Тогда, если время работы программы без отказа t отсчитывается от точки t = 0, а τ остается фиксированным, функция надежности, или вероятность безотказной работы на интервале от 0 до t, равна
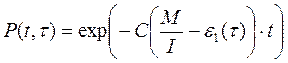 (22)
(22)
 (23)
(23)
Нам необходимо найти начальное значение ошибок M и коэффициент пропорциональности С. Эти неизвестные оцениваются путем пропуска функционального теста в двух точках переменной оси отладки ta и tв, выбранных так, что ε1(ta)<ε1(td).
В процессе тестирования собирается информация о времени и количестве ошибок на каждом прогоне, т.е. общее время тестирования τ складывается из времени каждого прогона:
τ = τ1 + τ2 + τ3 + … + τn.
Предполагая, что интенсивность появления ошибок постоянна и равна λ, можно вычислить ее как число ошибок в единицу времени,
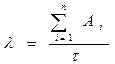 (24)
(24)
где Ai - количество ошибок на i - ом прогоне.
Тогда 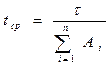 . (25)
. (25)
Имея данные для двух различных моментов тестирования ta и tв, можно сопоставить уравнения (23) при τa и τb:
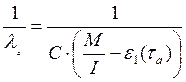 (26)
(26)
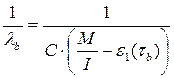 (27)
(27)
Из соотношений (26) и (27) найдем неизвестные параметры С и М:
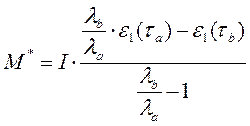 (28)
(28)
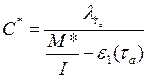 (29)
(29)
Получив неизвестные M* и C*, можно рассчитать надежность программы по формуле (22).
Пример 6.
Программа содержит 2 000 командных строк, из них, до начала эксплуатации (после периода отладки), 15 командных строк содержат ошибки. После 20 дней работы обнаружена 1 ошибка. Найти среднее время безошибочной работы программы и интенсивность отказов программы при коэффициенте пропорциональности, равном 0,7.
| I=2000 | |
| M=15 | |
| t=20 | |
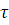 =1 =1
| |
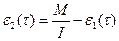 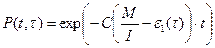 C=0,7 C=0,7
| |
e1=1/2000=0,0005;
e2=(15/2000)-0,0005=0,007;
P(t)=exp(-0,7*(15/2000-0,0005)*20))=0,90661 - функция надежност;
tср=1/0,7*(15/2000-0,0005)=204,0816;
 =0,0049 – интенсивность появления ошибок.
=0,0049 – интенсивность появления ошибок.
Пример 7.
На условиях примера 3 определить вероятность безошибочной работы программы в течение 90 суток.
P(t)=exp(-0,7*(15/2000-0,0005)*90))=0,643393.
2.5. Марковские и пуассоновские модели надежности
Марковский процесс характеризуется дискретным временем и конечным множеством состояний. Временной параметр пробегает неотрицательные числовые значения, а процесс (цепочка) определяется набором вероятностей перехода 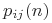 , т.е. вероятностью перейти на
, т.е. вероятностью перейти на 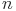 -шаге из состояния
-шаге из состояния 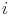 в состояние
в состояние 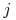 . Процесс называется однородным, если он не зависит от
. Процесс называется однородным, если он не зависит от 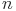 . В моделях, базирующихся на процессе Маркова, предполагается, что количество дефектов, обнаруженных в ПС, в любой момент времени зависит от поведения системы и представляется в виде стационарной цепи Маркова. При этом количество дефектов конечное, но является неизвестной величиной, которая задается для модели в виде константы. Интенсивность отказов в ПС или скорость прохода по цепи зависит лишь от количества дефектов, которые остались в ПС. К этой группе моделей относятся: Джелински- Моранды, Шика-Вулвертона, Шантикумера и др.
. В моделях, базирующихся на процессе Маркова, предполагается, что количество дефектов, обнаруженных в ПС, в любой момент времени зависит от поведения системы и представляется в виде стационарной цепи Маркова. При этом количество дефектов конечное, но является неизвестной величиной, которая задается для модели в виде константы. Интенсивность отказов в ПС или скорость прохода по цепи зависит лишь от количества дефектов, которые остались в ПС. К этой группе моделей относятся: Джелински- Моранды, Шика-Вулвертона, Шантикумера и др.
Ниже рассматриваются некоторые модели надежности, которые обеспечивают рост надежности ПО, находят широкое применение на этапе тестирования и описывают процесс обнаружения отказов при следующих предположениях:
- все ошибки в ПС не зависят друг от друга с точки зрения локализации отказов;
- интенсивность отказов пропорциональна текущему числу ошибок в ПС (убывает при тестировании программного обеспечения);
- вероятность локализации отказов остается постоянной;
- локализованные ошибки устраняются до того, как тестирование будет продолжено;
- при устранении ошибок новые ошибки не вносятся.
Приведем основные обозначения величин при описании моделей роста надежности:
-
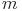 - число обнаруженных отказов ПО за время тестирования;
- число обнаруженных отказов ПО за время тестирования; -
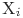 - интервалы времени между отказами
- интервалы времени между отказами 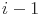 и
и 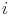 , при
, при 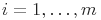 ;
; -
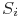 - моменты времени отказов (длительность тестирования до
- моменты времени отказов (длительность тестирования до 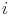 -отказа),
-отказа), 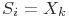 при
при 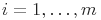 ;
; -
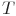 - продолжительность тестирования ПО (время, для которого определяется надежность);
- продолжительность тестирования ПО (время, для которого определяется надежность); -
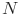 - оценка числа ошибок в ПО в начале тестирования;
- оценка числа ошибок в ПО в начале тестирования; -
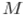 - оценка числа прогнозированных ошибок;
- оценка числа прогнозированных ошибок; -
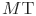 - оценка среднего времени до следующего отказа;
- оценка среднего времени до следующего отказа; -
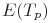 - оценка среднего времени до завершения тестирования;
- оценка среднего времени до завершения тестирования; -
 - оценка дисперсии;
- оценка дисперсии; -
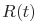 - функция надежности ПО;
- функция надежности ПО; -
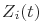 - функция риска в момент времени
- функция риска в момент времени  между
между 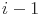 и
и 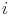 -отказами;
-отказами; -
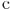 - коэффициент пропорциональности;
- коэффициент пропорциональности; -
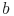 - частота обнаружения ошибок.
- частота обнаружения ошибок.
Далее рассматриваются несколько моделей роста надежности, основанные на этих предположениях и использовании результатов тестирования программ в части отказов, времени между ними и др.
Модель Джелинского-Моранды.
В этой модели используются исходные данные, приведенные выше, а также:
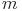 - число обнаруженных отказов за время тестирования;
- число обнаруженных отказов за время тестирования;
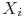 - интервалы времени между отказами;
- интервалы времени между отказами;
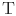 - продолжительность тестирования.
- продолжительность тестирования.
Функция риска 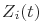 в момент времени
в момент времени  расположена между
расположена между 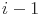 и
и 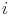 имеет вид:
имеет вид:
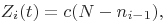 (30)
(30)
где 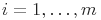 ;
; 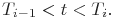
Эта функция считается ступенчатой кусочнопостоянной функцией с постоянным коэффициентом пропорциональности и величиной ступени - 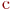 . Оценка параметров
. Оценка параметров 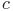 и
и 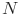 производится с помощью системы уравнений:
производится с помощью системы уравнений:
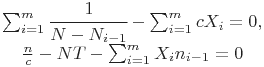 (31)
(31)
При этом суммарное время тестирования вычисляется так: 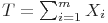
Выходные показатели для оценки надежности относительно указанного времени 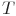 включают:
включают:
- число оставшихся ошибок
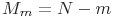 ;
; - среднее время до текущего отказа
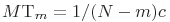 ;
; - среднее время до завершения тестирования и его дисперсию
Функция надежности вычисляется по формуле:
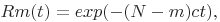 (32)
(32)
при 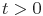 и числе ошибок, найденных и исправленных на каждом интервале тестирования, равным единице.
и числе ошибок, найденных и исправленных на каждом интервале тестирования, равным единице.
Модель Шика-Вулвертона.
Модель используется тогда, когда интенсивность отказов пропорциональна не только текущему числу ошибок, но и времени, прошедшему с момента последнего отказа. Исходные данные для этой модели аналогичны выше рассмотренной модели Джелински-Моранды:
-
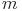 - число обнаруженных отказов за время тестирования,
- число обнаруженных отказов за время тестирования, -
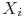 - интервалы времени между отказами,
- интервалы времени между отказами, -
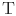 - продолжительность тестирования.
- продолжительность тестирования.
Функции риска 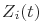 в момент времени между
в момент времени между 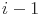 и
и 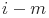 отказами определяются следующим образом:
отказами определяются следующим образом:
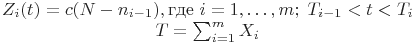 (33)
(33)
Эта функция является линейной внутри каждого интервала времени между отказами, возрастает с меньшим углом наклона. Оценка c и N вычисляется из системы уравнений:
К выходным показателям надежности относительно продолжительности 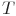 относятся:
относятся:
- число оставшихся ошибок
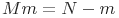 ;
; - среднее время до следующего отказа MTт = (р / (2 (N - m) c))1/2;
- среднее время до завершения тестирования и его дисперсия
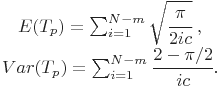 (34)
(34)
Функция надежности вычисляется по формуле:
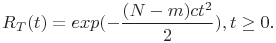 (35)
(35)
Модели пуассоновского типа базируются на выявлении отказов и моделируются неоднородным процессом, который задает 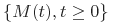 - неоднородный пуассоновский процесс с функцией интенсивности
- неоднородный пуассоновский процесс с функцией интенсивности 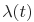 , что соответствует общему количеству отказов ПС за время его использования
, что соответствует общему количеству отказов ПС за время его использования  .
.
Модель Гоело-Окумото.
В основе этой модели лежит описание процесса обнаружения ошибок с помощью неоднородного пуассоновского процесса, ее можно рассматривать как модель экспоненциального роста. В этой модели интенсивность отказов также зависит от времени. Кроме того, в ней количество выявленных ошибок трактуется как случайная величина, значение которой зависит от теста и других условных факторов.
Исходные данные этой модели:
-
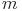 - число обнаруженных отказов за время тестирования;
- число обнаруженных отказов за время тестирования; -
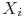 - интервалы времени между отказами;
- интервалы времени между отказами; -
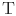 - продолжительность тестирования.
- продолжительность тестирования.
Функция среднего числа отказов, обнаруженных к моменту  , имеет вид
, имеет вид
 (36)
(36)
где 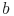 - интенсивность обнаружения отказов и показатель роста надежности
- интенсивность обнаружения отказов и показатель роста надежности 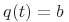 .
.
Функция интенсивности 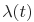 в зависимости от времени работы до отказа равна
в зависимости от времени работы до отказа равна
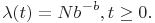 (37)
(37)
Оценка 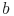 и
и 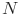 получаются из решения уравнений:
получаются из решения уравнений:
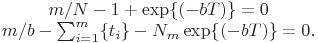 (38)
(38)
Выходные показатели надежности относительно времени 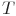 определяют:
определяют:
1. среднее число ошибок, которые были обнаружены в интервале  , по формуле
, по формуле 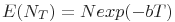 ,
,
2. функцию надежности
 ()
()
В этой модели обнаружение ошибки трактуется как случайная величина, значение которой зависит от теста и операционной среды.
В других моделях количество обнаруженных ошибок рассматривается как константа. В моделях роста надежности исходной информацией для расчета надежности являются интервалы времени между отказами тестируемой программы, число отказов и время, для которого определяется надежность программы при отказе. На основании этой информации по моделям определяются показатели надежности вида:
- вероятность безотказной работы;
- среднее время до следующего отказа;
- число необнаруженных отказов (ошибок);
- среднее время дополнительного тестирования программы.
Модель анализа результатов прогона тестов использует в своих расчетах общее число экспериментов тестирования и число отказов. Эта модель определяет только вероятность безотказной работы программы и выбрана для случаев, когда предыдущие модели нельзя использовать (мало данных, некорректность вычислений). Формула определения вероятности безотказной работы по числу проведенных экспериментов имеет вид
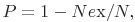
где 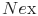 - число ошибочных экспериментов,
- число ошибочных экспериментов, 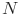 - число проведенных экспериментов для проверки работы ПС.
- число проведенных экспериментов для проверки работы ПС.
Таким образом, можно сделать вывод о том, что модели надежности ПС основаны на времени функционирования и/или количестве отказов (ошибок), полученных в программах в процессе их тестирования или эксплуатации. Модели надежности учитывают случайный марковский и пуассоновский характер соответственно процессов обнаружения ошибок в программах, а также характер и интенсивность отказов.
Заключение
В результате проделанной работы можно сделать вывод, что:
1. качество программного обеспечения – это совокупность характеристик ПО, относящихся к его способности удовлетворять установленные и предполагаемые потребности;
2. существует большое количество метрик и моделей для определения качества программного обеспечения. Каждая имеет свои уникальные характеристики и определенное назначение;
3. тщательно проведенный метрический анализ качества в соответствии с целями разработки создает основу для корректного планирования и контроля затрат на качество для достижения требуемых показателей и эффективности использования ресурсов.
Для того чтобы поддерживать конкурентоспособность своей организации разработчики ПО должны применять все более эффективные, рентабельные методы, технологии, инструментальные средства, способствующие постоянному повышению качества и более совершенному удовлетворению потребителей ПО.
Литература
1. http://met-rix.narod.ru/page1.htm (17.10.2011, 19:45);
2. http://www.pmprofy.ru/content/rus/67/675-article.asp (21.10.2011, 20:15);
3. http://www.intuit.ru/department/se/swebok/10/3.html (10.11.2011, 21:05);
4. http://www.internet-law.ru/gosts/gost/18984/ (15.11. 2011, 18:10);
5. http://turboreferat.ru/information/modeli-nadezhnosti-programmnogo-obespecheniya/14510-78630-page2.html (15.11.2011, 18:15);
6. http://www.viva64.com/ru/a/0045/ (13.12.2011, 22:30);
7. http://www.cmcons.com/articles/CC_CQ/dev_metrics/mertics_part_1/ (12.12.2011, 21:30);
8. http://www.ibm.com/developerworks/ru/edu/0108novich/section2.html (12.12.2011, 21:45);
9. http://gdznet.com/userhelps/metriki-koda-i-ix-prakticheskaya-realizaciya-v- subversion-i-clearcase-chast-1-metriki.html (13.12.2011, 22:00);
10. http://ru.wikipedia.org/wiki/ (22.11.2011, 20:20);
11. http://abc.vvsu.ru/Books/ebooks_iskt/ (10.12.2011, 15:20).
Date: 2015-07-17; view: 9560; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |