Законы распределений времени до отказа

2.1. Что такое критерий и показатель надежности

Критерием называется признак (мерило), по которому оценивается надежность. Например, вероятность безотказной работы Р(t), интенсивность отказов λ(t), средняя наработка на отказ Т.

Основными характеристиками критериев являются:

- научность;

- полнота оценки надежности технического объекта;

- вычисляемость;

- наглядность;

- непротиворечивость иным критериям качества объекта;

- возможность применения для оценки других, более общих показателей технического объекта (например, эффективность, безопасность, живучесть, риск).

Показателем надежности называется численное значение критерия. Например, вероятность безотказной работы в течение 1000 часов равна 0,95, т. е. Р(1000) = 0,95, или средняя наработка на отказ равна 687 часов, Т = 687 час.

Показатели задаются в технических требованиях на изделие, рассчитываются в процессе проектирования, оцениваются в процессе испытания и эксплуатации технического объекта.

Разработка критериев, методов анализа техники по критериям надежности, методов испытания и обработки их результатов — это задачи глубоко научные. Расчеты показателей надежности, способы их обеспечения в процессе проектирования и создания, сбор данных об отказах техники в процессе испытания и эксплуатации - это инженерное дело.

Надежность является сложным физическим свойством, поэтому не существует одного обобщенного критерия и показателя, который бы достаточно полно характеризовал надежность техники. Только семейство критериев позволяет оценить надежность сложной технической системы. Выбор критериев зависит от типа технического объекта, его назначения и требуемой полноты оценки надежности.

Между показателями надежности существуют однозначные математические зависимости в виде формул. Поэтому при разработке семейства показателей надежности нельзя их задавать в виде равенств. Например, нельзя формулировать требования на надежность в таком виде: вероятность безотказной работы в течение 150 часов должна быть равна 0,97, а среднее время безотказной работы Т = 650 час. Такие требования могут оказаться противоречивыми.

Рассмотрим критерии надежности невосстанавливаемых и восстанавливаемых систем.

2.2. Критерии надежности невосстанавливаемых систем

Отказ элемента является событием случайным, а время ξдо его возникновения - случайной величиной. Основной характеристикой надежности элемента является функция распределения продолжительности его безотказной работы F(t)=P(ξ < t), определенная при t≥0. На ее основе могут быть получены следующие показатели надежности невосстанавливаемого элемента:

- Р(t) — вероятность его безотказной работы в течение времени t;

- Q(t) = 1 - Р(t) — вероятность отказа в течение времени t;

- T₁ — среднее время безотказной работы (средняя наработка до отказа);

f(t) — плотность распределения времени безотказной работы;

- λ(t) — интенсивность отказа в момент времени t;

- Λ(t) — функция ресурса;

- t_γ - γ-процентный ресурс - наработка, в течение которой элемент не достигает состояния отказа с вероятностью γ/100.

Рассмотрим эти показатели более подробно. Дадим вероятностные и статистические определения, укажем на их свойства, достоинства и недостатки.

2.2.1. Вероятность безотказной работы

Вероятностью безотказной работы называется вероятность того, что технический объект не откажет в течение времени t или что время ξ, работы до отказа технического объекта больше времени его функционирования t:

Р(t) = Р( ξ >t). (2.1)

Вероятность безотказной работы является убывающей функцией времени, имеющей следующие свойства:

0≤Р(t)≤1, Р(0)=1, Р(+∞) = 0.

По статистическим данным об отказах, полученным из опыта или эксплуатации, Р(t) определяется следующей статистической-оценкой:

(2.2)

где N₀ — общее число образцов, находящихся на испытании, N(t) — число исправно работающих образцов в момент времени t, n(t) – число отказавших образцов в течение времени t. Здесь и далее звездочкой обозначаются величины, полученные по статистическим данным.

Вероятность безотказной работы имеет следующие достоинства:

- характеризует надежность во времени, являясь интервальной оценкой;

- определяет многие важные показатели техники, например эффективность, безопасность, живучесть, риск;

- сравнительно просто вычисляется и определяется по статистическим данным об отказах техники;

- достаточно полно характеризует надежность невосстанавливаемой техники.

Основной недостаток этого критерия - ограниченность применения. Вероятность безотказной работы характеризует надежность невосстанавливаемой техники или восстанавливаемой до первого ее отказа.

2.2.2. Плотность распределения времени безотказной работы (частота отказов)

Плотность распределения времени безотказной работы f(t) - это плотность распределения случайной величины ξ. Она наиболее полно характеризует надежность техники в данный момент (точечная характеристика). По ней можно определить любой показатель надежности невосстанавливаемой системы. В этом основное достоинство плотности распределения времени безотказной работы.

Статистически f(t) определяется отношением числа отказавших образцов техники в единицу времени к числу испытуемых образцов при условии, что отказавшие образцы не восполняются исправными:

(2.3)

n(t,t+Δt) - число отказавших образцов за промежуток времени [ t,t+Δt ], N₀ — число образцов, первоначально поставленных на испытания.

Действительно, т. к. f(t) = Q '(t) = -P'(t), то для малых значений Δt имеем

Пусть N(t) — число исправно работающих образцов к моменту времени t, N(t,+Δt) - число образцов, исправно работающих к моменту (t,+Δt). Поскольку

то

что совпадает с выражением (2.3), т. к. N(t) - N(t + Δt) = n(t, t + Δt).

2.2.3. Интенсивность отказов

Интенсивностью отказов называется отношение плотности распределения к вероятности безотказной работы объекта:

(2.4)

Статистически интенсивность отказов есть отношение числа отказавших образцов техники в единицу времени к среднему числу образцов, исправно работающих на интервале [ t,t+Δt ]:

(2.5)

где -среднее число исправно работающих образцов на интервале [ t,t+Δt ]. Соотношение (2.5) для малых Δt следует непосредственно из (2.2) и (2.3).

На основе определения интенсивности отказов (2.4) имеет место равенство

(2.6)

Интегрируя (2.6), получим

или

Интенсивность отказов λ(t) является основным показателем надежности элементов сложных систем. Это объясняется следующими обстоятельствами:

- надежность многих элементов можно оценить одним числом, т. к. интенсивность отказа элементов - величина постоянная;

- по известной интенсивности λ(t) наиболее просто оценить остальные показатели надежности как элементов, так и сложных систем;

- λ(t) обладает хорошей наглядностью;

- интенсивность отказов нетрудно получить экспериментально.

Опыт эксплуатации сложных систем показывает, что изменение интенсивности отказов λ(t) большого количества объектов описывается U-образной кривой (рис. 2.1). Время можно условно разделить на три характерных участка:

1. Период приработки.

2. Период нормальной эксплуатации.

3. Период старения объекта.

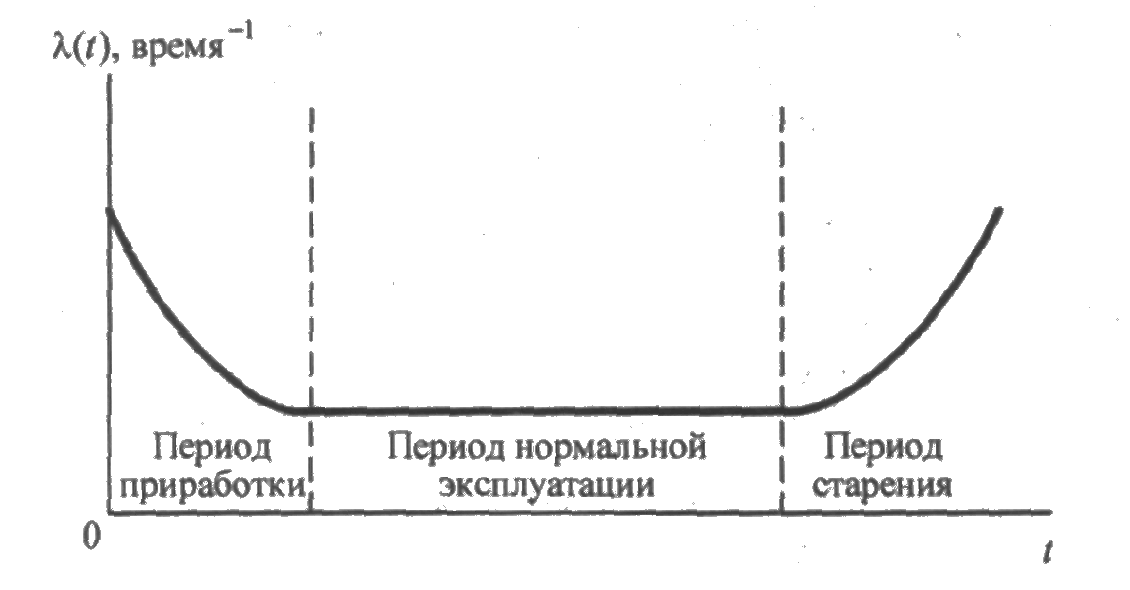
Рис. 2.1. U - образный вид кривой интенсивности отказов

Период приработки объекта имеет повышенную интенсивность отказов, вызванную приработочными отказами, обусловленными дефектами производства, монтажа и наладки. Иногда с окончанием этого периода связывают гарантийное обслуживание объекта, когда устранение отказов производится изготовителем. В период нормальной эксплуатации интенсивность отказов практически остается постоянной, при этом отказы носят случайный характер и появляются внезапно, прежде всего из-за случайных изменений нагрузки несоблюдения условий эксплуатации, неблагоприятных внешних факторов и т.п. Именно этот период соответствует основному времени эксплуатации объекта. Возрастание интенсивности отказов относится к периоду старения объекта и вызвано увеличением числа отказов из-за износа, старения и других причин, связанных с длительной эксплуатацией.

2.2.4. Среднее время безотказной работы

Средним временем безотказной работы Т₁ называется математическое ожидание времени безотказной работы технического объекта:

T₁=M(ξ). (2.7)

По статистическим данным об отказах T₁ определяется следующей зависимостью:

(2.8)

где N₀ — число испытуемых образцов техники, t_i — время безотказной работы i -го образца.

Как математическое ожидание случайной величины с плотностью f(t), среднее время безотказной работы вычисляется по формуле:

Интегрируя (2.9) по частям, получим

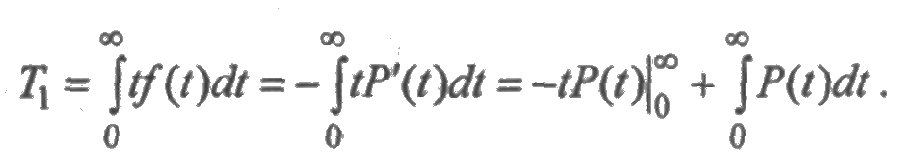
Первое слагаемое равно нулю, т. к. Р(0)=1, Р(+∞) = 0, и тогда выражение для Т₁ будет иметь вид:

Среднее время безотказной работы является интегральным показателем надежности. Его основное достоинство - высокая наглядность. Недостаток этого показателя в том, что он, будучи интегральным, характеризует надеж­ность техники длительного времени работы.

Итак, между показателями надежности существуют следующие зависимости:

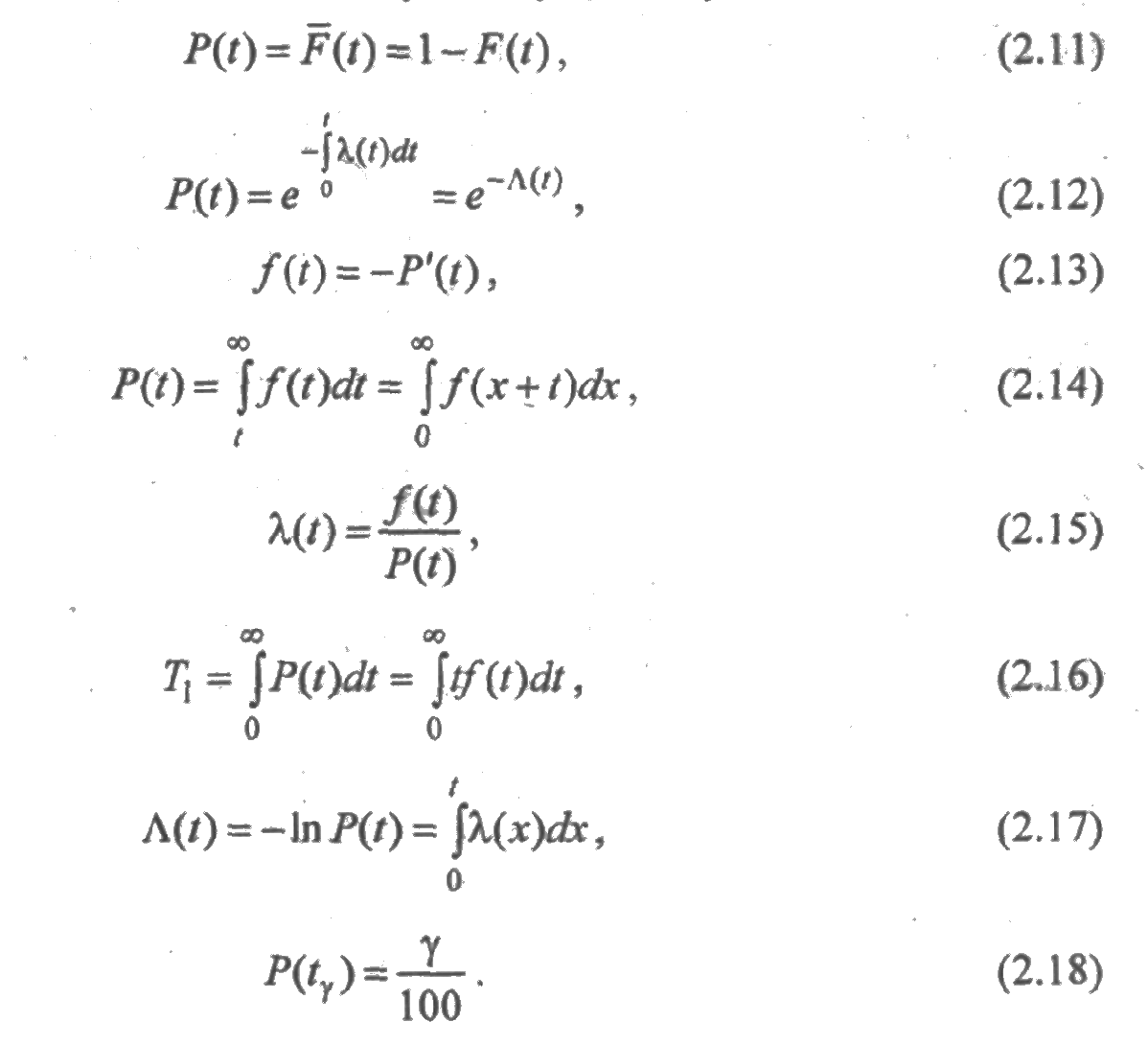
ПРИМЕР 2.1. На испытании находилось N₀=100 образцов техники. Данные об их отказах приведены в первых трех строках табл. 2.1.

Необходимо вычислить показатели надежности: P(t), f(t), λ(t), T ₁.

Решение.

Вычислим P(t). Будем иметь в виду, что нам достоверно неизвестен момент отказа на промежутке длины Δt. Поэтому будем предполагать, что отказы происходят в середине этого промежутка, т. е. в моменты времени: t = 50,150,250 и т. д. На первом интервале произошел один отказ. Тогда согласно (2.2) вероятность безотказной работы будет:

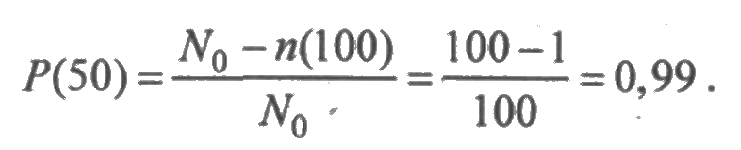
На втором участке произошло 2 отказа, а вcего за два периода длины Δt — 3 отказа. Тогда

Результаты расчетов приведены в четвертой строке табл. 2.1

Вычисления значений f(t) выполним по формуле (2.3):

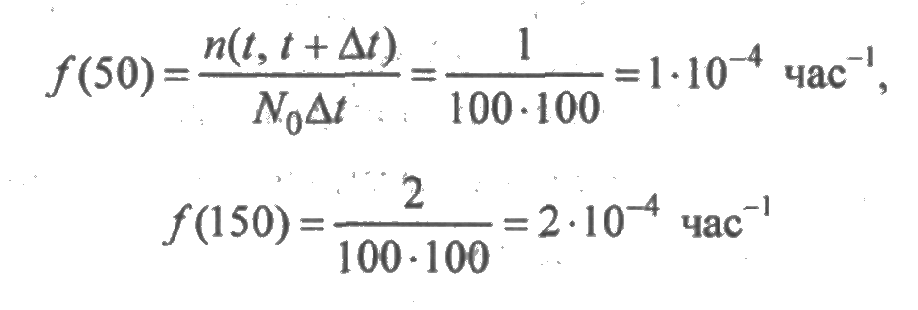
и т. д. В данном случае число отказов на промежутке длины Δt не суммируется с числом отказов на предыдущих участках, т. к. функция f(t) является точечной. Результаты расчетов приведены в пятой строке табл. 2.1.

Вычислим значения λ(t), воспользовавшись выражением (2.5). На первом участке произошел один отказ, при этом в начале участка число исправных образцов N₀ (0) = N₀ = 100, а в конце участка N₀ (0) = N₀-1 = 99. Тогда

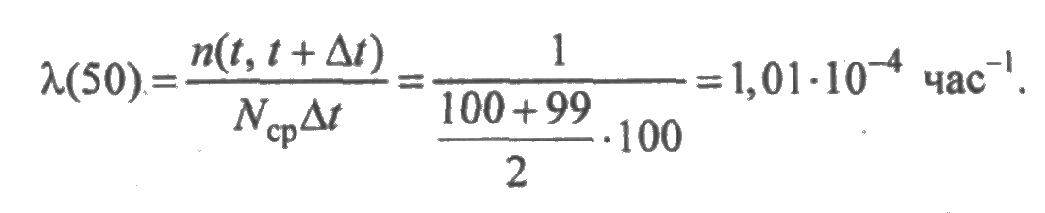
Аналогично на втором участке

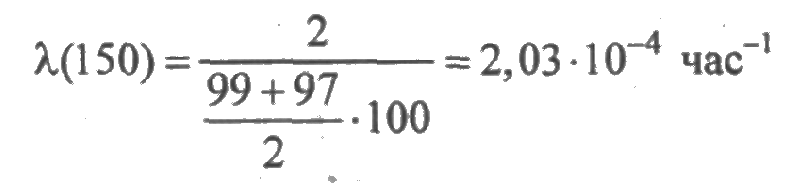
и т. д. Значения λ(t) приведены в последней строке табл. 2.1.

Вычислим среднее время безотказной работы по формуле (2.8):

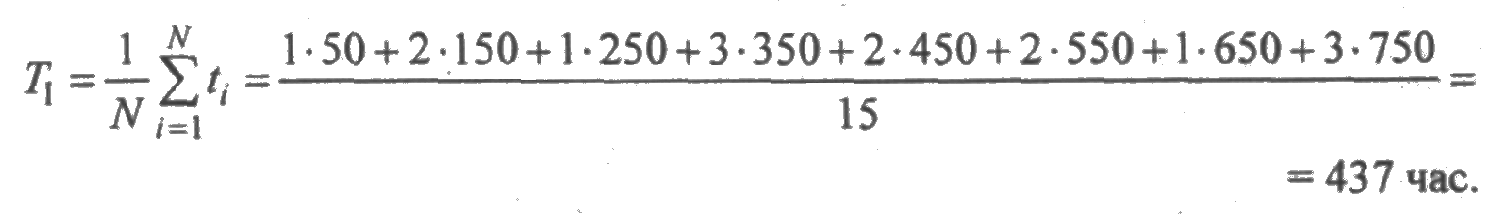
В данном случае испытания закончены при отказе 15 из 100 образцов.

Очевидно, что полученный результат существенно ниже действительного значения среднего времени безотказной работы как математического ожидания случайной величины.

2.3. Критерии надежности восстанавливаемых систем

Показателями надежности восстанавливаемых элементов и систем могут быть также показатели надежности невосстанавливаемых элементов. Это имеет место в тех случаях, когда система, в состав которой входит элемент, является неремонтируемой по условиям ее работы (необитаемый космический аппарат, аппаратура, работающая в агрессивных средах, самолет в процессе полета, отсутствие запчастей для ремонта и т. п.). Надежность восстанавливаемых объектов оценивают следующими показателями:

- Т — среднее время работы между отказами (средняя наработка на отказ);

- T _в — среднее время восстановления;

- ω(t) — параметр потока отказов;

- К_г(t) — функция готовности — вероятность того, что система исправна в момент t;

- К_п(t) — функция простоя— вероятность того, что в момент t система неисправна и восстанавливается;

- К_г — коэффициент готовности— вероятность того, что система будет исправной при длительной эксплуатации (стационарный режим);

- К_п — коэффициент простоя — вероятность того, что система будет неисправной при длительной эксплуатации.

Рассмотрим эти показатели несколько подробнее.

2.3.1. Среднее время работы между отказами и среднее время восстановления

Среднее время между отказами Т определяется отношением средней суммарной наработки к среднему числу отказов при длительной работе объекта. Среднее время восстановления Т _в определяется отношением среднего суммарного времени восстановления к среднему числу восстановлений при дли­тельной работе объекта. Данные определения обсуждаются далее в разд. 2.6.

По статистическим данным среднее время между отказами вычисляется по формуле:

(2.19)

где t_i — время между отказами i -го образца, полученное при условии, что испытания ведутся с восстановлением отказавших образцов техники или их заменой. В этом случае число испытуемых образцов техники N₀ остается постоянным.

4.1.1. Параметр потока отказов

Параметром потока отказов ω(t) называется производная (скорость изменения) среднего числа отказов объекта в момент t.

Статистически параметр потока отказов определяется как отношение числа отказавших образцов техники в единицу времени к числу образцов, поставленных на испытание при условии, что отказавшие образцы заменяются исправными или отремонтированными:

где п(t, t + Δt) — число отказавших образцов за промежуток времени [ t, t + Δt ], N₀ — число образцов, первоначально поставленных на испытания.

Параметр потока отказов обладает следующими свойствами:

- в случае экспоненциального закона времени работы объекта (см. разд. 2.4) с параметром λ, и мгновенного восстановления ω(t) ≡ λ;

- при мгновенном восстановлении предел, к которому стремится параметр потока отказов при t→∞, равен величине, обратной среднему времени безотказной работы, т. е.

- при мгновенном восстановлении параметр потока отказов и плотность распределения времени до отказа связаны следующим интегральным уравнением Вольтерра второго рода:

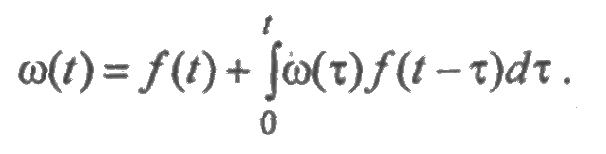
Это уравнение устанавливает зависимость между показателями надежности восстанавливаемой и невосстанавливаемой техники. Оно позволяет определить по статистическим данным об отказах восстанавливаемой техники в процессе ее эксплуатации показатели надежности невосстанавли­ваемой техники (см. гл. 11).

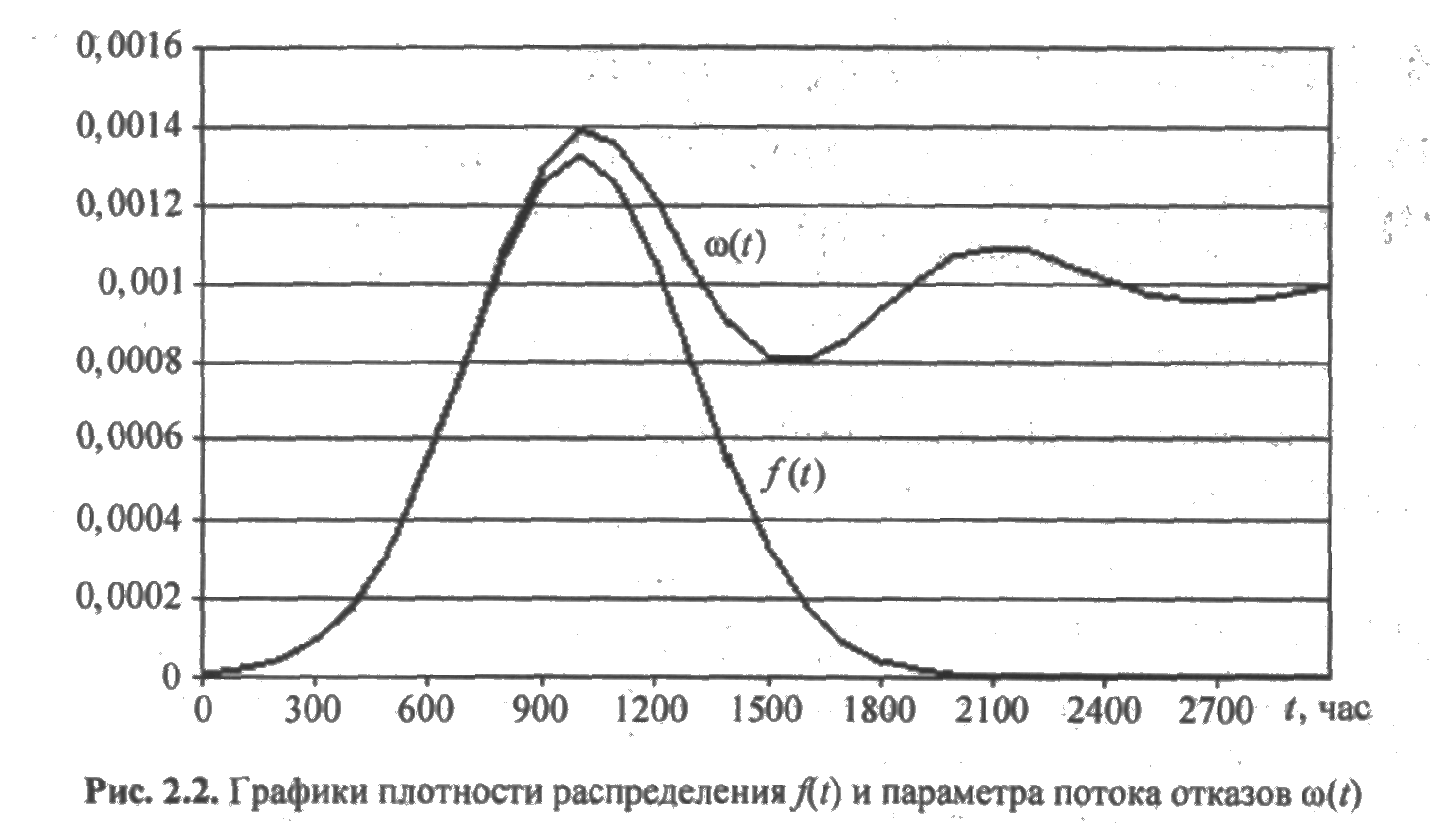
ПРИМЕР 2.2. Время до отказа объекта имеет нормальное распределение с математическим ожиданием Т = 1000 час и средним квадратическим отклонением s = 300 час ???. Привести графическую иллюстрацию плотности распределения f(t) и параметра потока отказов ω(t).

Решение. Графики функций изображены на рис. 2.2. Параметр потока отказов ω(t) получен путем численного решения уравнения Вольтерра.

Для относительно небольшого времени функционирования объекта параметр потока отказов близок к плотности распределения, но при длительной работе плотность распределения стремится к нулю, тогда как параметр потока отказов приближается к своему стационарному значению, равному 1/ T = 0,001 час^-1.

2.3.3. Функция готовности и функция простоя

Функцией готовности К_г(t) называется вероятность того, что восстанавливаемая система исправна в момент времени t.

Функцией простоя К_п(t) называется вероятность того, что в момент времени t система находится в отказовом состоянии (в ремонте).

Приведем основные зависимости между введенными показателями:

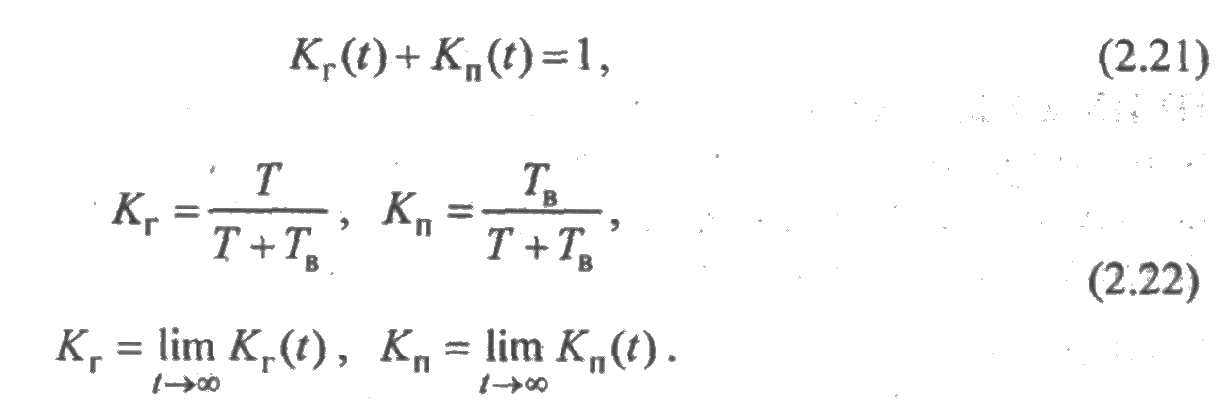
Данные показатели являются наиболее важными для восстанавливаемых элементов и систем. Другие, более специфические показатели, их определения и расчетные соотношения будут приведены в разд. 2.6.

2.4. Законы распределения времени до отказа, наиболее часто используемые в теории надежности

Приведем наиболее часто используемые в теории надежности параметрические семейства распределений случайной величины ξ, т.е. распределений, зависящих от одного или нескольких параметров, Функция

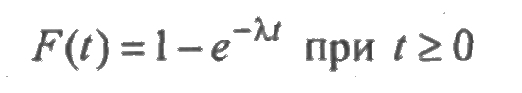
задает экспоненциальное (или показательное) распределение. Экспоненциальным законом распределения можно аппроксимировать время безотказной работы большого числа элементов. В первую очередь это относится к элементам радиоэлектронной аппаратуры, а также к машинам, эксплуатируемым в период после окончания приработки и до существенного проявления посте­пенных отказов. Экспоненциальное распределение применяется в областях, связанных с "временем жизни": в медицине - продолжительность жизни больных; в надежности - продолжительность безотказной работы устройства; в психологии - время, затраченное на выполнение тестовых задач. Оно используется в задачах массового обслуживания, в которых речь идет об интервалах времени между телефонными звонками, или между моментами поступления техники в ремонтную мастерскую, или между моментами обращения клиентов.

Это распределение имеет один параметр λ=1/ T₁, где T₁ — средняя наработка элемента до отказа. Таким образом, параметр λ характеризует число отказов элемента в единицу времени и называется интенсивностью отказов, он имеет размерность (время)^-1, например, час^-1 или лет^-1.

Плотность экспоненциального распределения задается как:

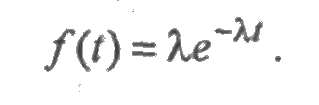
Функция надежности

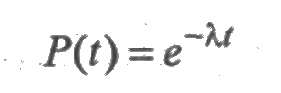
определяет вероятность безотказной работы за время t (рис. 2.3). В данном случае интенсивность отказов есть величина постоянная λ (t) = λ.

Функция ресурса для экспоненциального распределения является линейной Λ(t) = λt.

Величина γ-процентного ресурса определяется по формуле

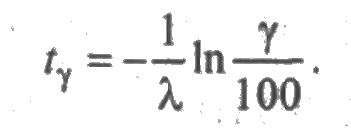
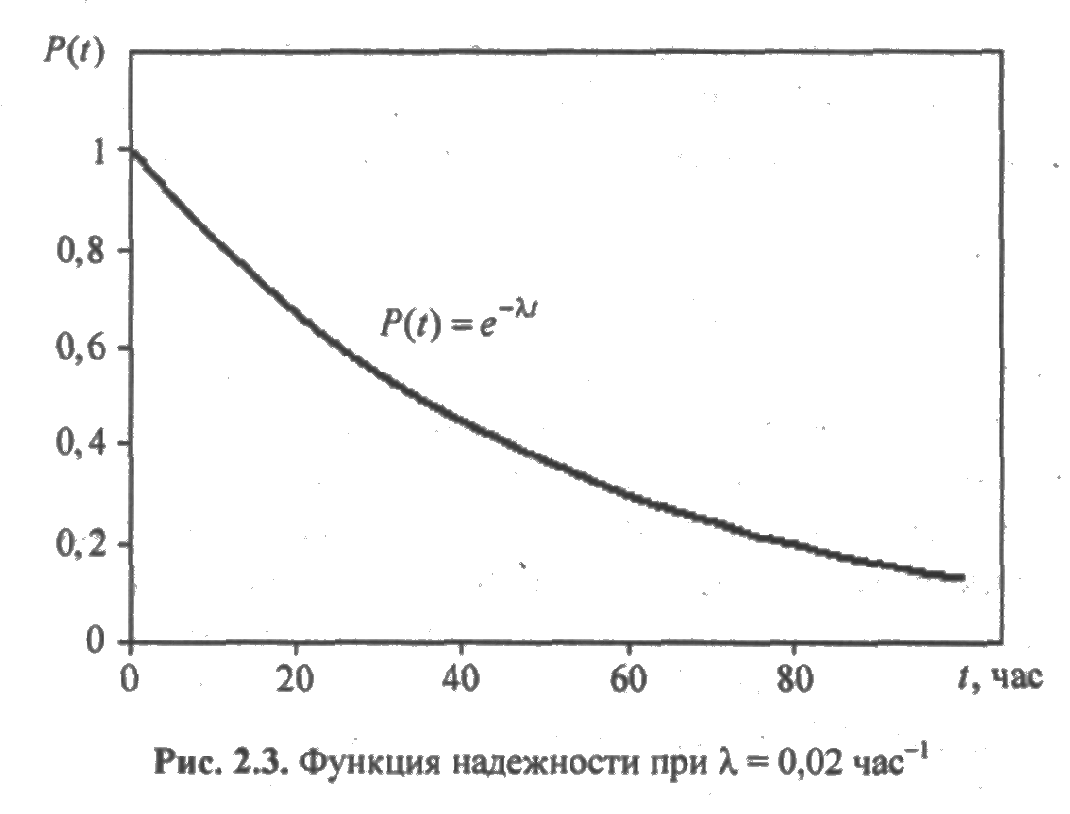
ПРИМЕР 2.3. Время безотказной работы элемента подчинено экспоненциальному распределению с параметром λ = 0,02 час^-1. Найти вероятность того что элемент проработает безотказно в течение 10 часов и в течение 50 часов.

Решение. Используя функцию надежности Р(t)=е^-λt, получим

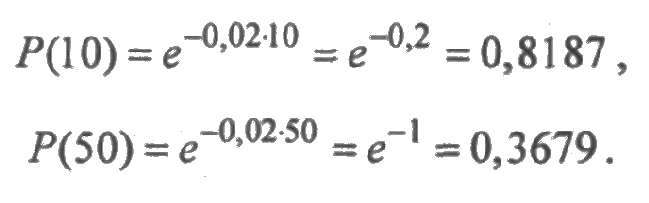
Экспоненциальное распределение выделяется среди других распределение свойством "отсутствия памяти". Пусть X — время службы некоторого изделия с экспоненциальным законом распределения. "Отсутствие памяти" означает, что изделие, проработавшее время t, имеет такое же распределение, что и новое, только что начавшее работу. Математически это свойство выра­жается в виде следующего равенства:

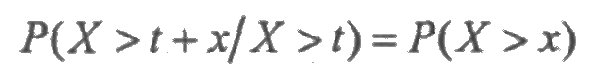
для любых t, х ≥0. Данное свойство как бы исключает износ и старение изделия.

Числовые характеристики экспоненциального распределения выражаются через его параметр: математическое ожидание М(Х)=1/λ, дисперсия D(X)=1/λ², среднее квадратическое отклонение s(X)=1/λ ????????.

Итак, при экспоненциальном законе отказов, на основании формул (2.11)— (2.18), между показателями надежности невосстанавливаемых систем существуют следующие зависимости:

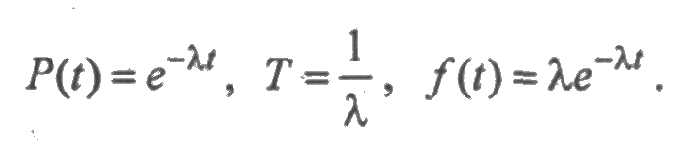
Для характеристики постепенных отказов обычно используют другие законы распределения.

Нормальное распределение (распределение Гаусса) определяется плотностью

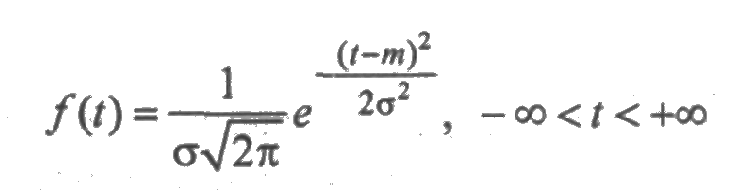
и зависит от двух параметров т и s, которые являются соответственно математическим ожиданием и средним квадратическим отклонением времени безотказной работы элемента. График плотности нормального распределения (кривая Гаусса) изображена на рис. 2.4.

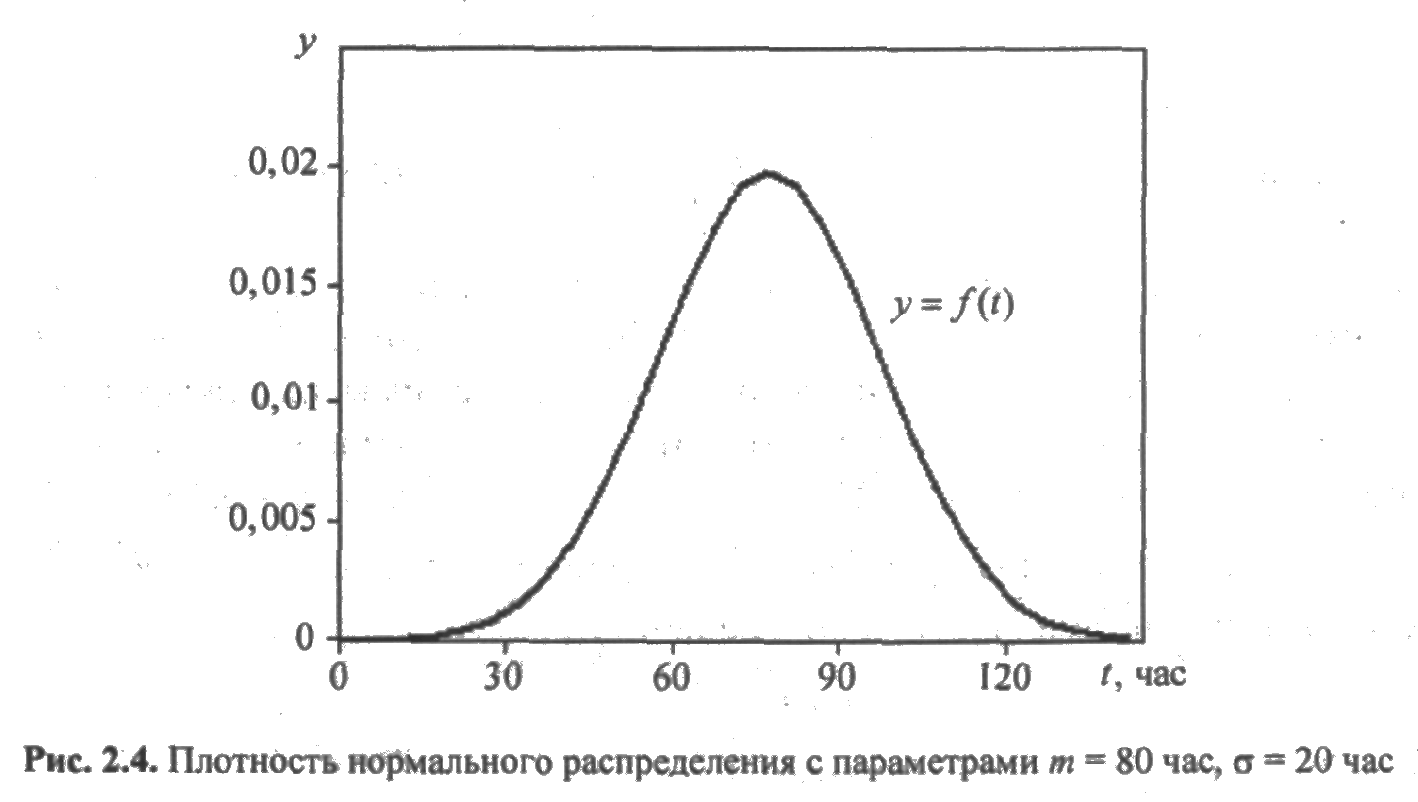
Согласно закону больших чисел, распределение всегда подчиняется нормальному закону, если на изменение случайной величины оказывают влияние многие примерно равнозначные факторы. Нормальному распределению подчиняются ошибки измерения деталей, дальность полета снарядов и т. п. При большом времени работы элемента и наличии восстановления среднее число отказов имеет асимптотически нормальное распределение.

Для нормального распределения функция надежности вычисляется по формуле:

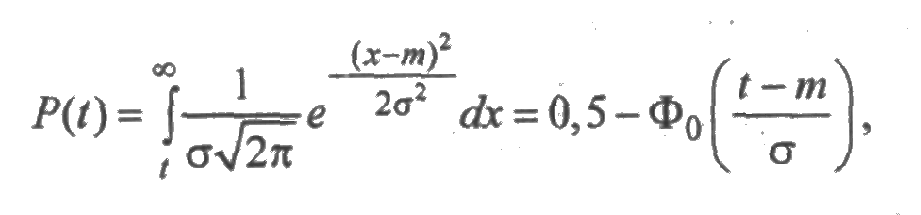
где 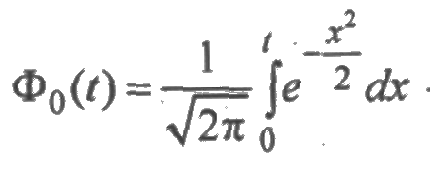— функция Лапласа, значения которой сведены в таблицы.

ПРИМЕР 2.4. Время безотказной работы элемента подчинено нормальному распределению с параметрами m =80 час и s=20 час. Найти вероятность того, что элемент проработает безотказно в течение 60 часов.

Решение. Так как для нормального распределения функция надежности равна

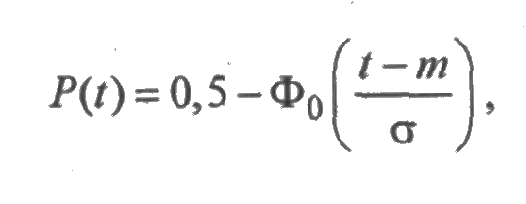
то

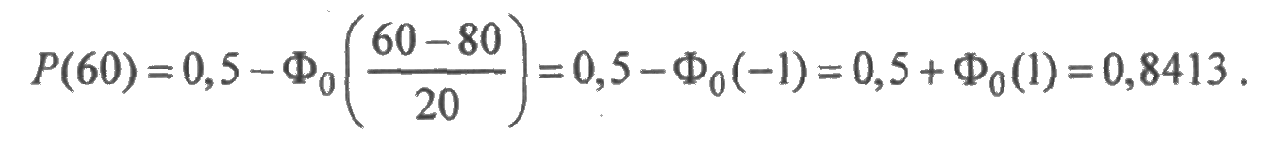
Отметим важное свойство нормального распределения: сумма независимых случайных величин, имеющих нормальное распределение, также распределена по нормальному закону. При этом параметры суммы выражаются через параметры слагаемых, а именно: математическое ожидание суммы равна сумме математических ожиданий, дисперсия суммы равна сумме дисперсий.

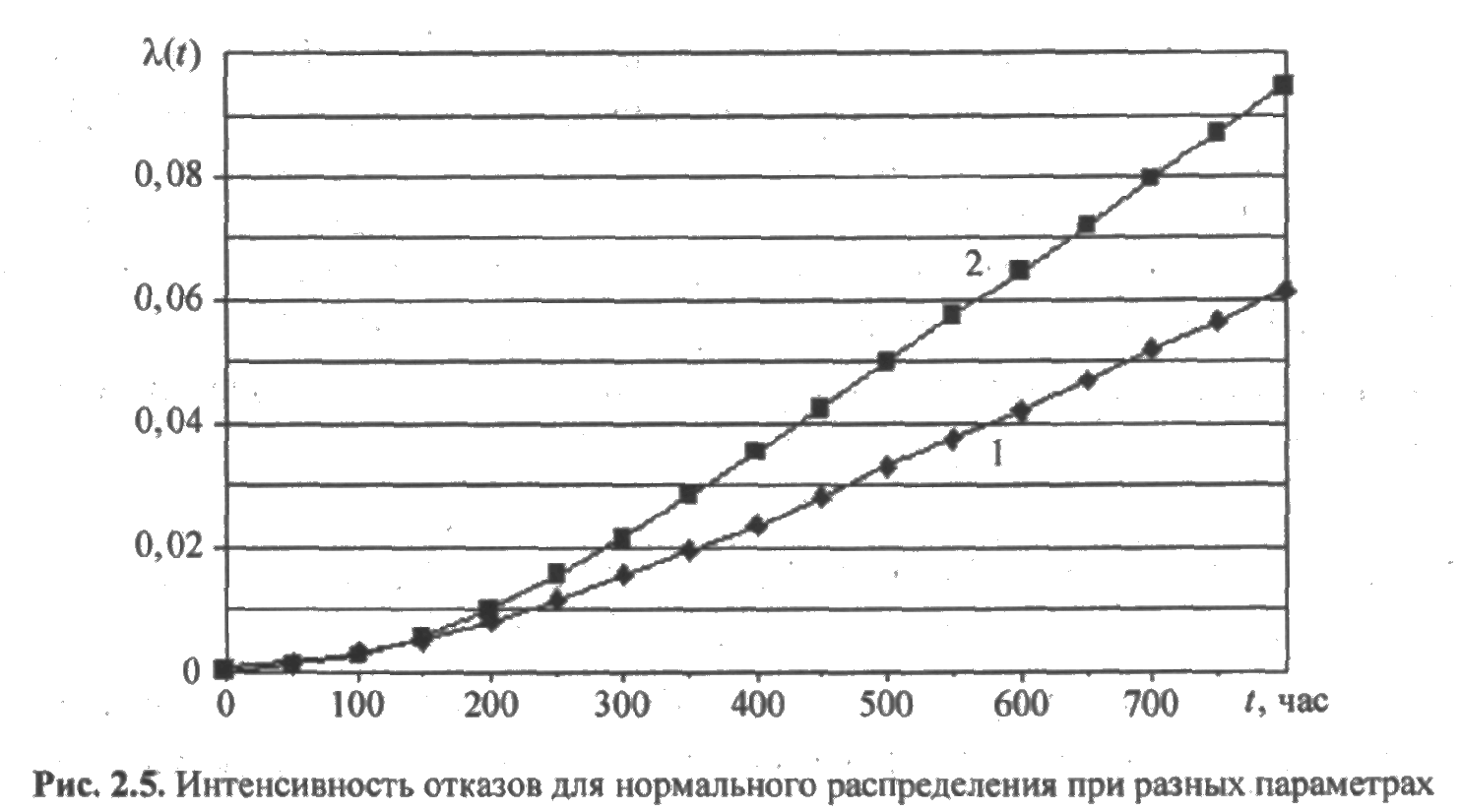
На рис. 2.5 представлены графики интенсивности отказов λ (t) для следующих параметров нормального распределения:

- т = 200 час и s = 100 час (кривая 1);

- т = 200 час и s = 80 час (кривая 2).

Усеченное нормальное распределение получается из нормального при огра­ничении интервала изменения случайной величины на промежуток [0,+∞). Плотность распределения записывается так же, как для нормального распределения, но с коэффициентом пропорциональности с:

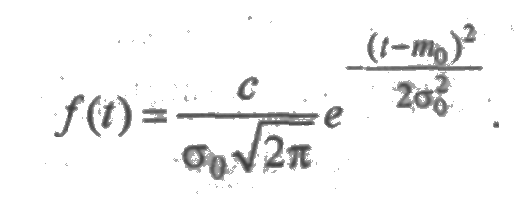
Усеченное нормальное распределение зависит от двух параметров m₀ и s₀, где m₀ — значение случайной величины, соответствующее максимальному значению f(t) и называемое модой. Коэффициент с определяется из усло­вия нормировки:

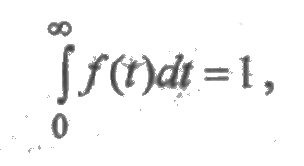
откуда

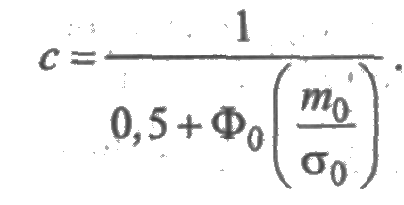
Математическое ожидание и среднее квадратическое отклонение усеченного нормального распределения определяются через параметры m₀ и s₀ по формулам:

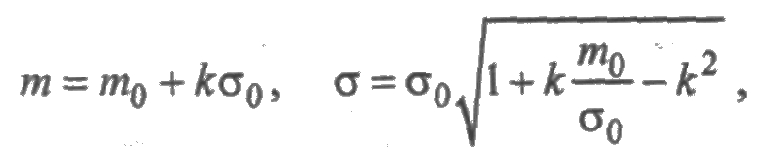
где

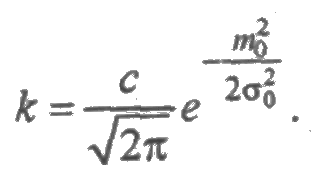
В логарифмически нормальном распределении логарифм случайной величины подчиняется нормальному закону с плотностью:

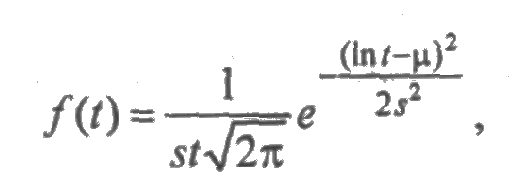
где μ и s — параметры распределения. Математическое ожидание и среднее квадратическое отклонение определяются в соответствии с формулами:

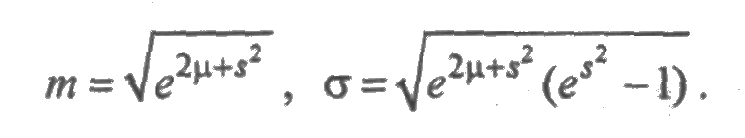
Логарифмически нормальное распределение применяют, например, для описания наработки подшипников качения. Вообще, оно удобно для описания случайных величин, представляющих собой произведение достаточно большого числа случайных величин, подобно тому, как нормальное распределение описывает сумму большого числа случайных величин.

Распределение Вейбулла является достаточно универсальным, благодаря возможности варьирования двух его параметров. Оно характеризуется плотностью распределения вероятностей:

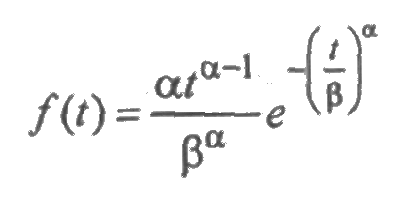
с параметром формы α и параметром масштаба β. Математическое ожидание и среднее квадратическое отклонение выражаются через эти параметры следующим образом:

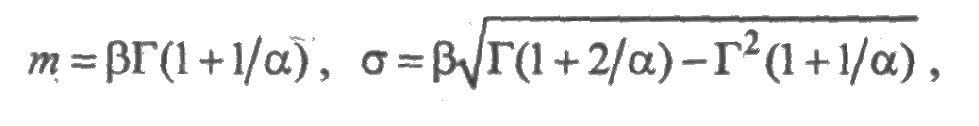
где

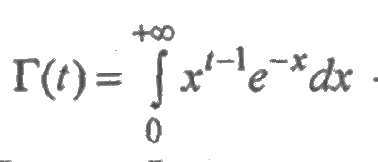
— гамма-функция. Универсальность распределения Вейбулла объясняется следующим: при α =1 распределение превращается в экспоненциальное; при α <1 функции плотности и интенсивности отказов убывающие; при α >1 интенсивность отказов возрастающая; при α =2 функция λ(t) линейная и распределение Вейбулла превращается в распределение Рэлея с плотностью:

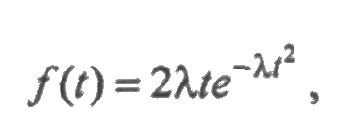
при α =3,3 распределение Вейбулла близко к нормальному. Наряду с логарифмически нормальным распределением, оно хорошо описывает наработку деталей по усталостным разрушениям, наработку до отказа подшипников, а также используется для оценки надежности деталей и узлов машин, в частности автомобилей, подъемно-транспортных и других машин.

Зависимости между показателями надежности в случае распределения Вейбулла имеют вид:

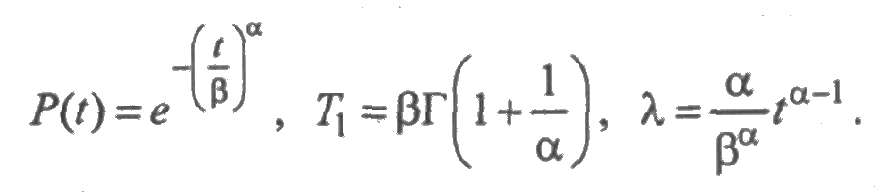
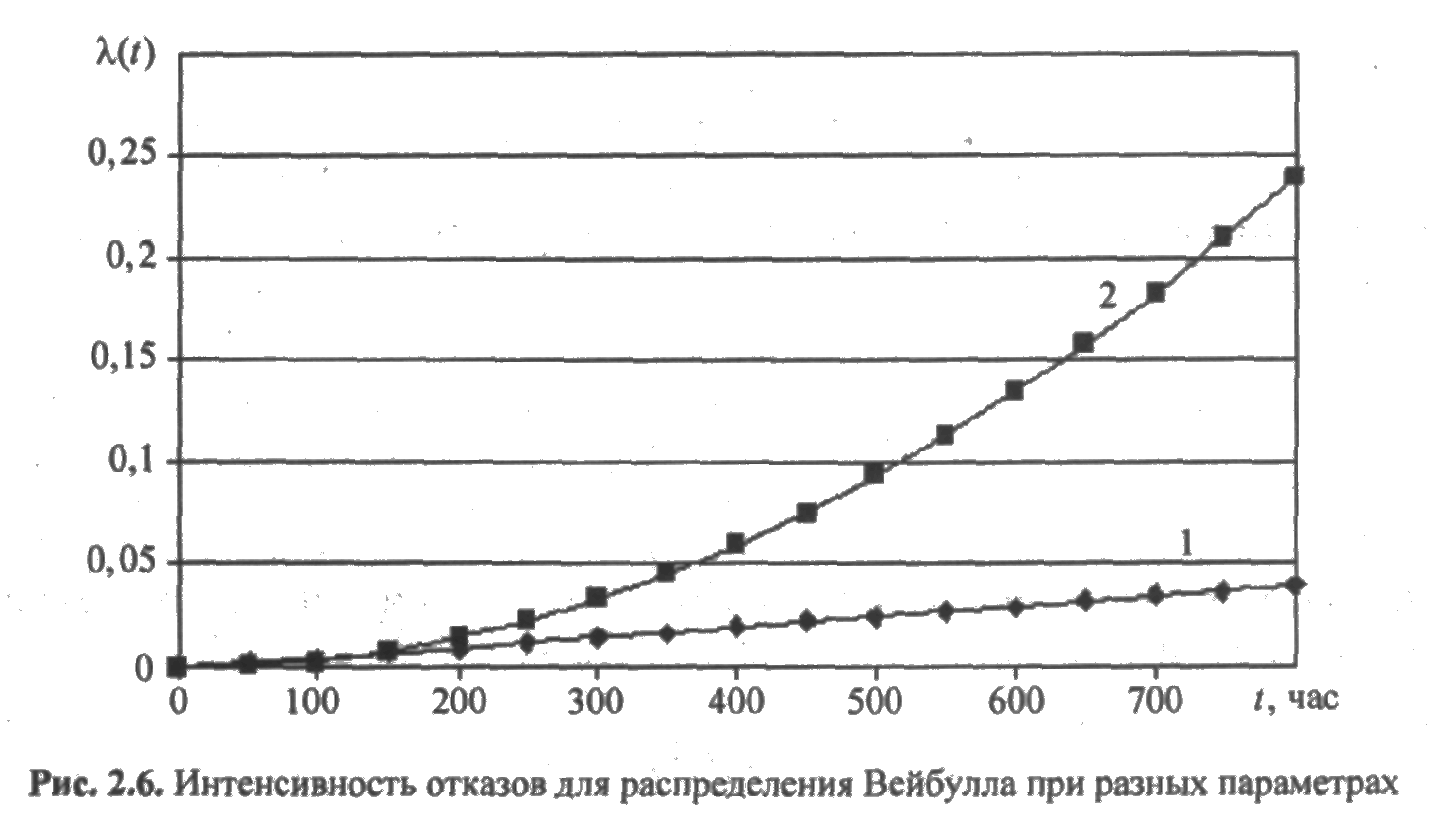
На рис. 2.6 представлены графики интенсивности отказов λ(t) для следующих параметров распределения Вейбулла:

- α = 2 и β = 200 час (кривая 1);

- α = 3 и β =200 час (кривая 2).

Гамма-распределение имеет плотность:

с параметрами α и β. Математическое ожидание и среднее квадратическое отклонение связаны с этими параметрами соотношениями:

Вероятность безотказной работы элемента, имеющего гамма-распределение, выражается через интеграл

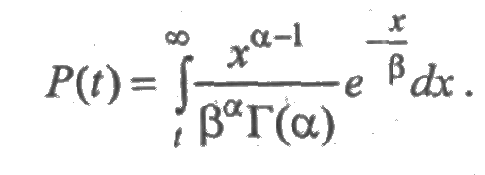
Параметр α, характеризующий асимметрию гамма-распределения, определяет вид характеристик надежности. При α > 1 интенсивность отказа возрастает, при α < 1 убывает, а при α = 1 становится постоянной, т. е. гамма-распределение превращается в экспоненциальное.

При целом α гамма-распределение называется распределением Эрланга порядка α. Сумма α случайных величин, имеющих экспоненциальное распределение с параметром λ, имеет распределение Эрланга с параметрами α и β=1/λ. Вероятность безотказной работы элемента, имеющего распределение Эрланга, равна

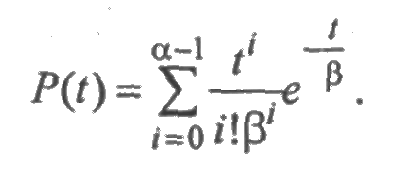
Зависимости между показателями надежности в случае гамма-распределения имеют вид:

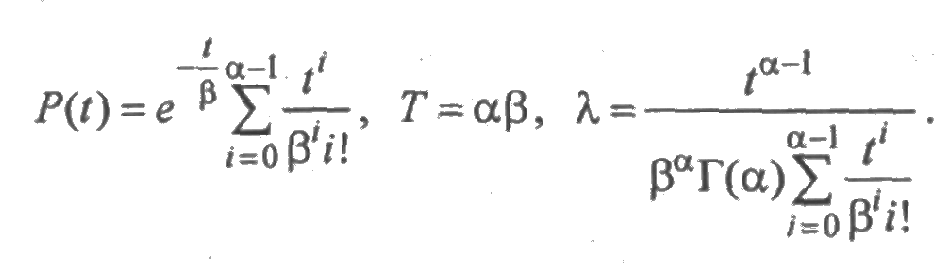
Смесь распределений определяется как линейная комбинация других распределений, например распределение с плотностью

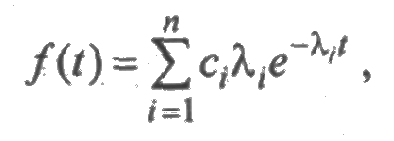
где образует смесь п экспоненциальных распределений. Такое распределение называется гиперэкспоненциальным.

Смесь гамма-распределений

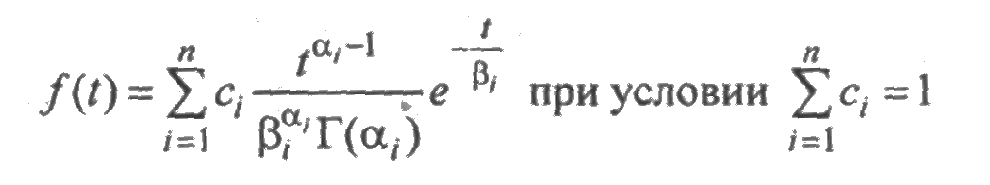
образует плотность обобщенного гамма-распределения и т. п.

Перечень полезных параметрических распределений можно продолжить. Например, если параметр λ экспоненциального распределения является случайной величиной, имеющей гамма-распределение с параметрами α и β, то в результате получается семейство распределений Парето с плотностью:

(?????????????)

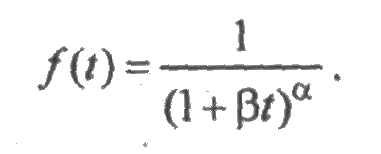При расчете надежности ряда изделий (рессор, подшипников и т. п.) применяют семейства распределений с дополнительным параметром сдвига или смещения. Так обобщением распределения Вейбулла является трехпараметрическое семейство распределений с плотностью:

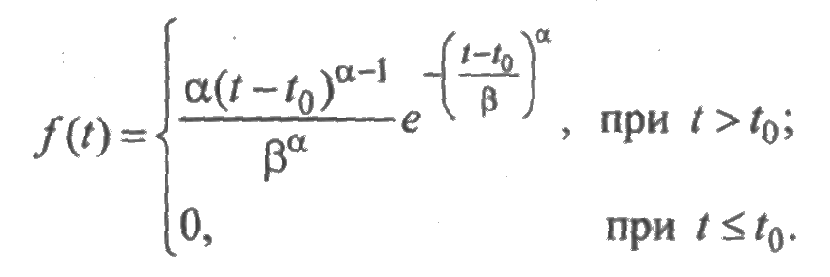
Параметр сдвига t₀ интерпретируется как гарантированное время безотказной работы.

Если элемент имеет перерывы в работе, то закон распределения времени до его отказа изменяется. Пусть — вероятность безотказной работы элемента, если бы он работал непрерывно. Предположим далее, что на непересекающихся интервалах [а_к;b_к], k = 1,2,...,п элемент простаивает, причем время простоя не влияет на его надежность. Тогда вероятность безотказной работы элемента при наличии интервалов простоя характеризуется параметрами смещения и выражается равенством:

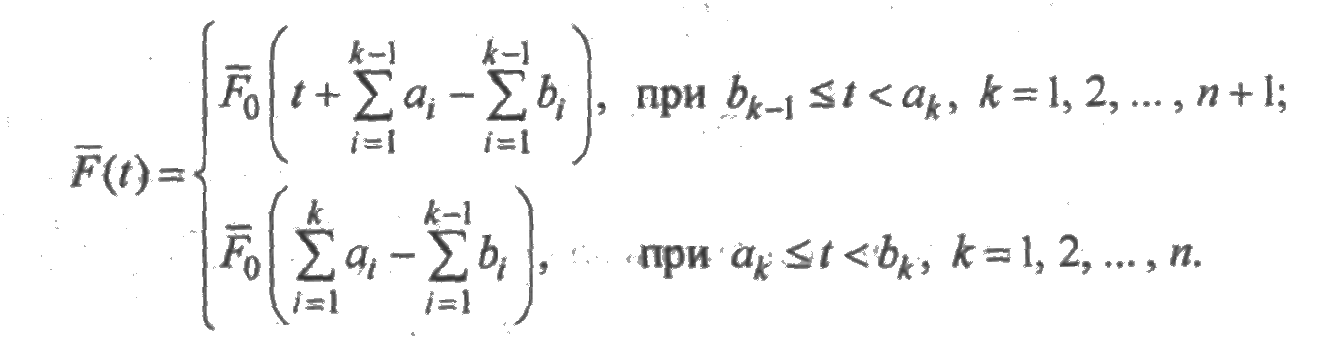
Здесь принято, что b₀ =0, а_n+1 = ∞.

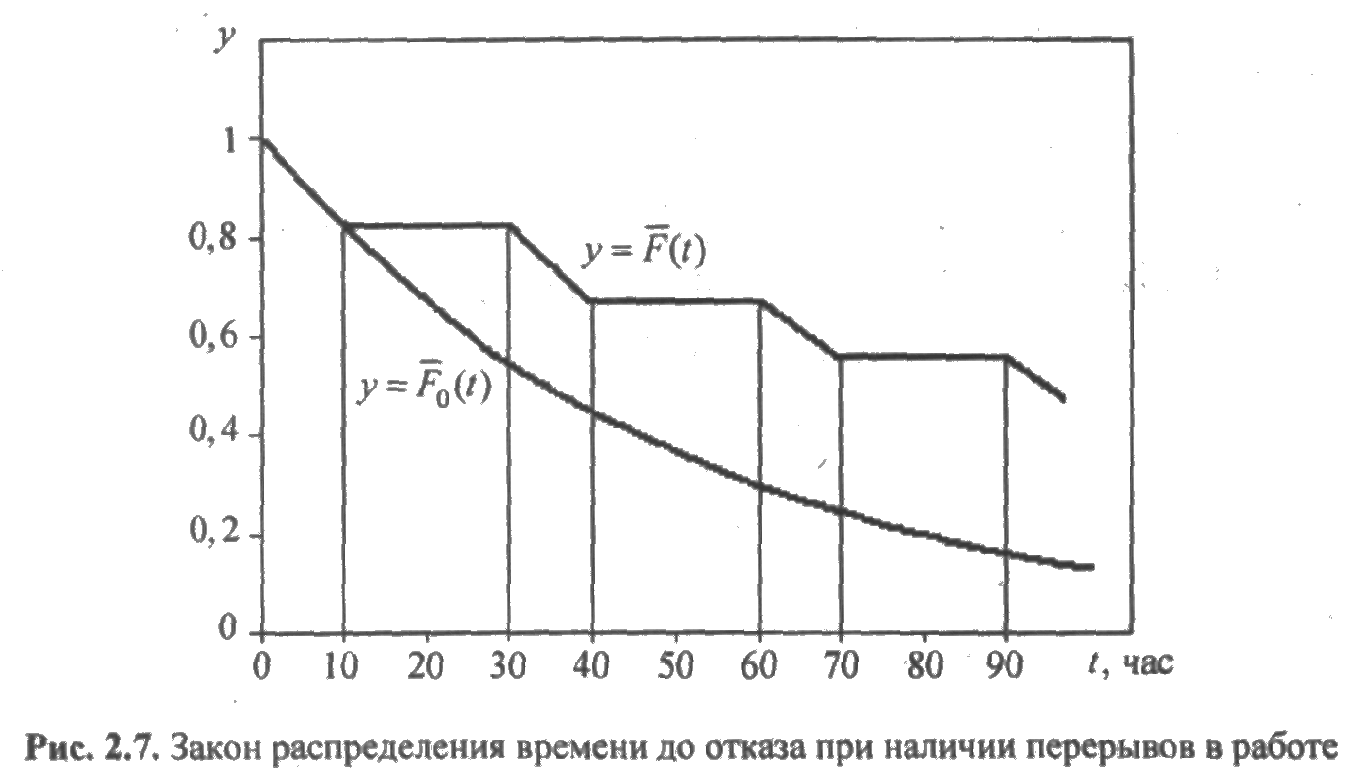
ПРИМЕР 2.5. Предположим, что график вероятности безотказной работы элемента у = имеет вид, изображенный на рис. 2.4. Пусть этот элемент работает только на временных интервалах [0; 10], [30; 40], (60; 70],..., а на остальных интервалах элемент простаивает. Требуется определить вероятность безотказной работы элемента у = с учетом простоя.

Решение. График искомой функции у = изображен на рис. 2.7. На интервалах простоя вероятность безотказной работы не уменьшается (функция постоянна), а на интервалах простоя график у = смещается вправо на величину, равную суммарному времени простоя элемента.

Заметим, что интервалы простоя могут быть как детерминированными, так и случайными. В последнем случае необходима информация о законах распределения а_к и b_к. Учет перерывов в работе элементов может существенно повлиять на надежность системы, образованной этими элементами.

2.5. Преобразование Лапласа

Многие числовые показатели надежности элементов и систем выражаются через функции типа свертки или бесконечными рядами, члены которых являются свертками функций. Для исследования таких показателей большую помощь может оказать преобразование Лапласа. Оно удобно также при расчетах предельных значений функций, лежит в основе операционного метода решения дифференциальных уравнений и систем. Преобразование Лапласа позволяет преобразовать любую систему обыкновенных дифференциальных уравнений в систему линейных алгебраических уравнений.

Пусть функция f(t) кусочно-непрерывна при t ≥0 и имеет ограниченный рост, т. е.

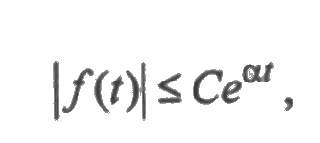
где С и α — некоторые постоянные. Тогда она называется оригиналом, а функция

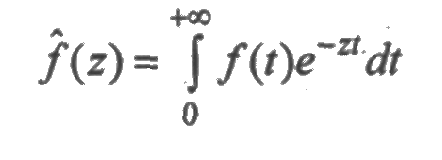
— ее изображением. Переход от оригинала к изображению называется преобразованием Лапласа, а переход от изображения к соответствующему оригиналу — обратным преобразованием Лапласа. В дальнейшем вместо будем иногда писать f(s).

Перечислим некоторые полезные свойства преобразования Лапласа.

1. Изображение линейной комбинации функций равно линейной комбинации изображений: если

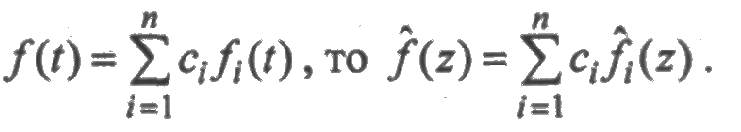
2. Изображением производной f '(t) является функция

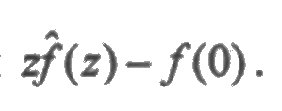
3. Изображение свертки функций равно произведению изображений сомножителей: если

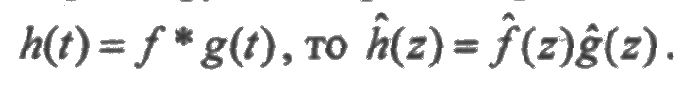
4. При вычислении предельных значений функций можно использовать равенство

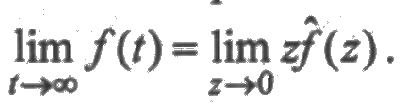
Заметим, что данное свойство не всегда верно. Так, например, если f(t) представляет собой сумму δ-функций, т. е.

то предел вообще не существует. Однако:

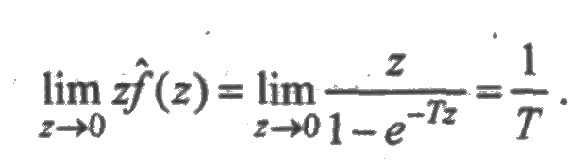
5. Если f(t) — плотность распределения вероятностей неотрицательной случайной величины X, то ее изображение удовлетворяет соотношениям:

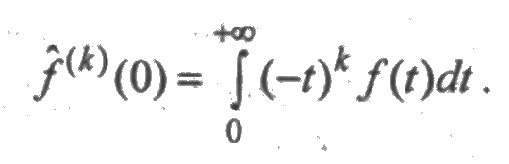
В частности,

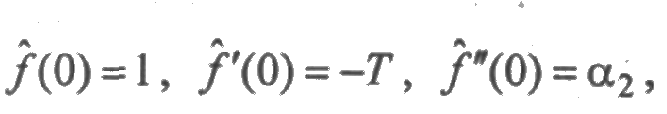
где Т — математичес ожидание, а α₂ — второй начальный момент случайной величины X.

Решение системы алгебраических уравнений, полученной по системе линейных дифференциальных уравнений, образуют дробно-рациональные функцию вида

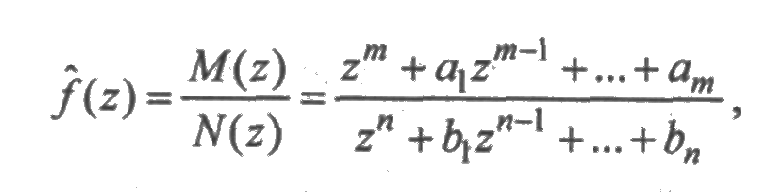
причем т<п. Если знаменатель дроби N(z) имеет только простые корни z ₁, z₂,..., z_n, то оригинал определяется равенством

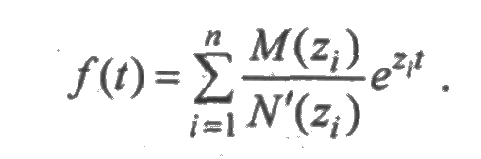
Если знаменатель дроби N(z) имеет кратные корни: z₁ кратности r₁, z₂ кратности z₂,..., z_k кратности r_k (r₁ + r₂ +...+ r_k = n), то оригинал определяется равенством

где коэффициенты А_ij находятся по формулам:

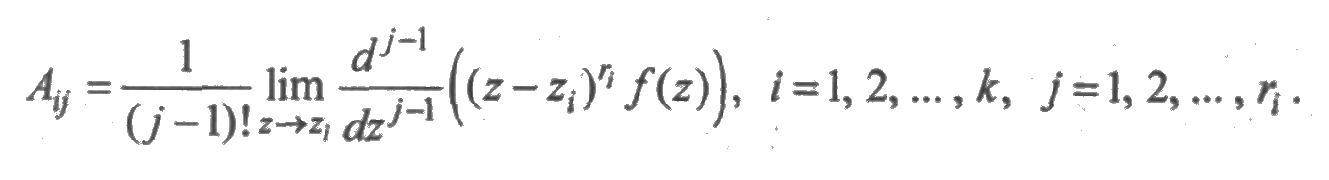
2.6. Специальные показатели надежности элементов и систем

2.6.1. Показатели надежности элемента

Работу восстанавливаемого элемента с двумя состояниями можно представить в виде последовательности интервалов исправной работы ξ_k и интервалов восстановления η_k, чередующихся друг за другом, как показано к рис. 2.8.

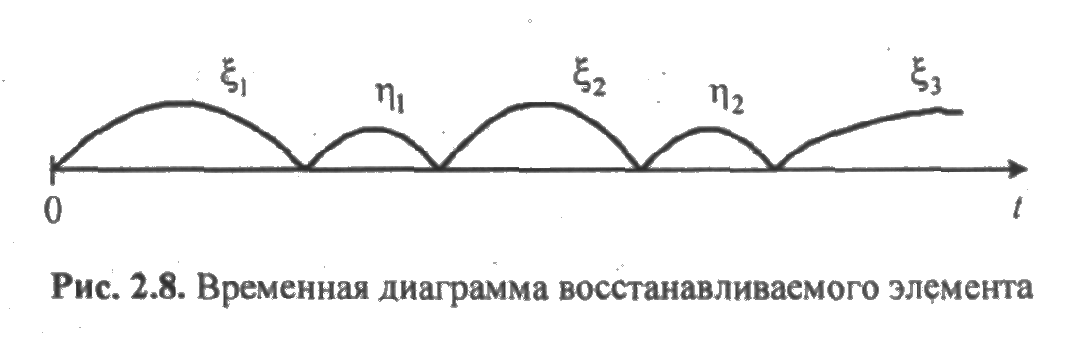
Предположим, что случайные величины ξ_k и η_k независимы и имеют плотности f_k(t) и g_k(t) соответственно. Обозначим через F_k(t) и G_k(t) функции распределения сумм соответственно, а через F_k,l(t) — функцию распределения суммы случайных величин Предположим также, что F₀(t) и G₀(t) = 1.

Рассмотрим следующие случайные процессы ζ(t) и ζ_B(t), равные соответственно числу отказов и числу восстановлений элемента за время [ 0; t ]. Это дискретные случайные процессы с непрерывным временем. Обозначим через М(t) = М(ζ(t)) и М_B(t)=M(ζ_B(t)) их математические ожидания (в предположении, что они существуют). Функции М(t) и М_B(t) характеризуют среднее число отказов и среднее число восстановлений элемента за время [0; t ]. Если в момент времени t =0 элемент был исправен, то очевидно, что М(t) ≥ М_B(t) для любого t.

Определим скорости изменения среднего числа отказов ω(t) = М'(t) и среднего числа восстановлений ω_в(t) = М'_B(t). Функции ω(t) и ω_в(t) называются параметрами потоков отказов и восстановлений соответственно. Принимая во внимание, что М(0) = М_B()) = 0, получим

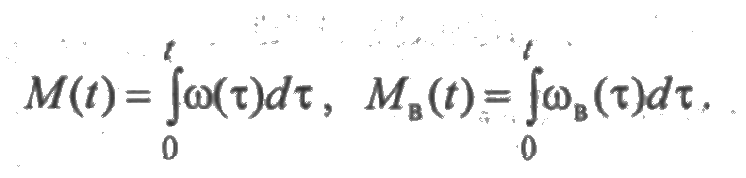
Рассмотрим случайный процесс χ(t), как суммарное время работы (наработка) элемента, и случайный процесс χ _в (t), как суммарное время восстановления элемента за время [0; t ]. Это есть непрерывные случайные процессы с непрерывным временем (на самом деле функции распределения в одной точке терпят разрыв). Обозначим через m(t) = М (χ(t)) и m _в (t) = М (χ _в (t)) - математические ожидания этих случайных процессов. Функции т(t) и т _в (t) показывают среднюю наработку и среднее суммарное время восстановлена элемента в течение времени [0;t]. Функция готовности К_г(t) и функция простоя К_П(t) элемента определяются как вероятности того, что в момент t элемент находится в состоянии работоспособности и в состоянии восстановления. Далее в этом разделе будет показано, что К_г(t) = т'(t), К_П(t)= т _в (t).

Разделив среднюю наработку на среднее число отказов элемента за время [ 0;t ], получим среднее время работы элемента между отказами, или наработку на отказ. Тогда среднее время работы элемента между отказами в течение времени [0; t ] определится отношением:

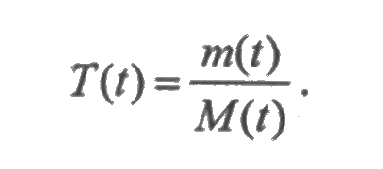
Аналогично определяется среднее время восстановления элемента в течение времени [0; t ], как отношение среднего суммарного времени восстановления элемента на среднее число восстановлений:

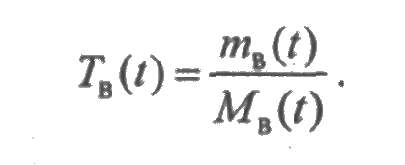
Интенсивности потоков отказов и восстановлений в момент t определим равенствами

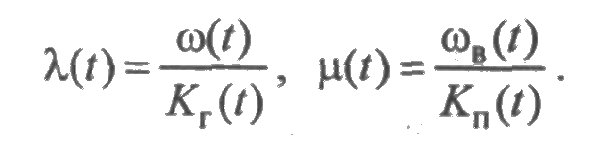
Получим представление введенных характеристик через плотности и функции распределения случайных величин ξ_k и η_k.

Любое сечение случайного процесса ζ(t) есть случайная величина дискретного типа с возможными значениями k =0,1,2,... и вероятностями р_k(t), Поскольку р_k(t) - вероятность того, что за время [0; t ] произошло ровно k отказов, то

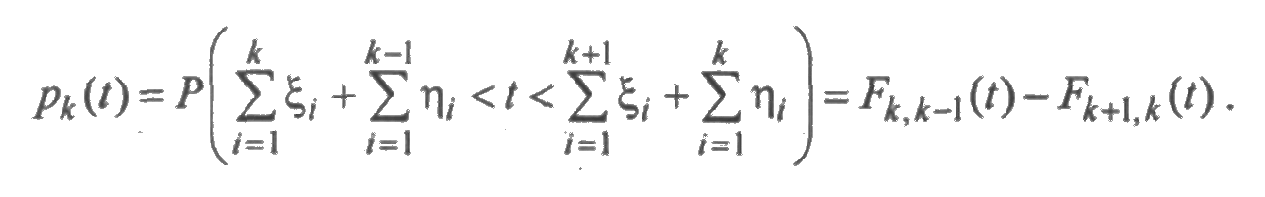
Поэтому математическое ожидание случайной величины ζ(t) равно

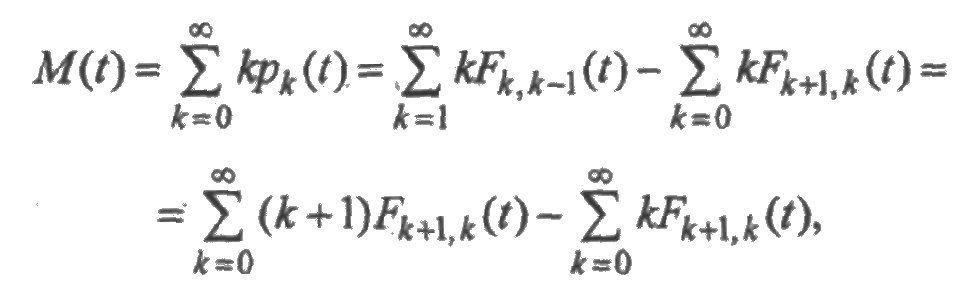
откуда

Аналогично для случайного процесса ζ_В(t) математическое ожидание равно

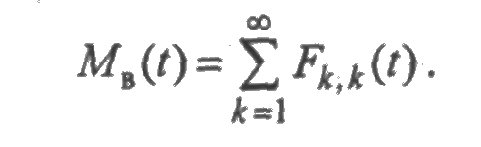
Параметры потоков ω (t) и ω_B (t) были определены как производные от математических ожиданий числа отказов и числа восстановлений элемента за промежуток времени [0; t ]. Дадим теперь иное, локальное в некотором смысле, но эквивалентное первоначальному, определение этих параметров. Пусть р(t,t + Δt) — вероятность отказа элемента за время [ t, t+Δt ], а р_B (t,t + Δt) — вероятность того, что за промежуток времени [ t,t + Δt ] элемент будет восстановлен. Тогда

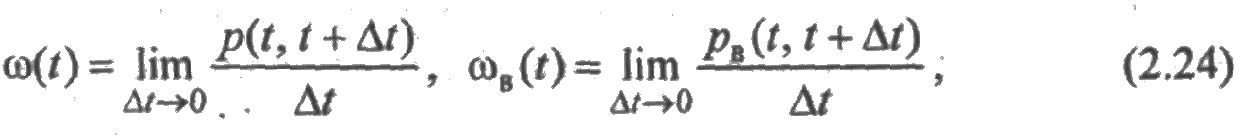
т. е. параметры потоков отказов и восстановлений равны соответственно вероятностям отказа и восстановления за малый промежуток времени, отнесенным к длине этого промежутка. Эквивалентность определений видна из следующих соотношений:

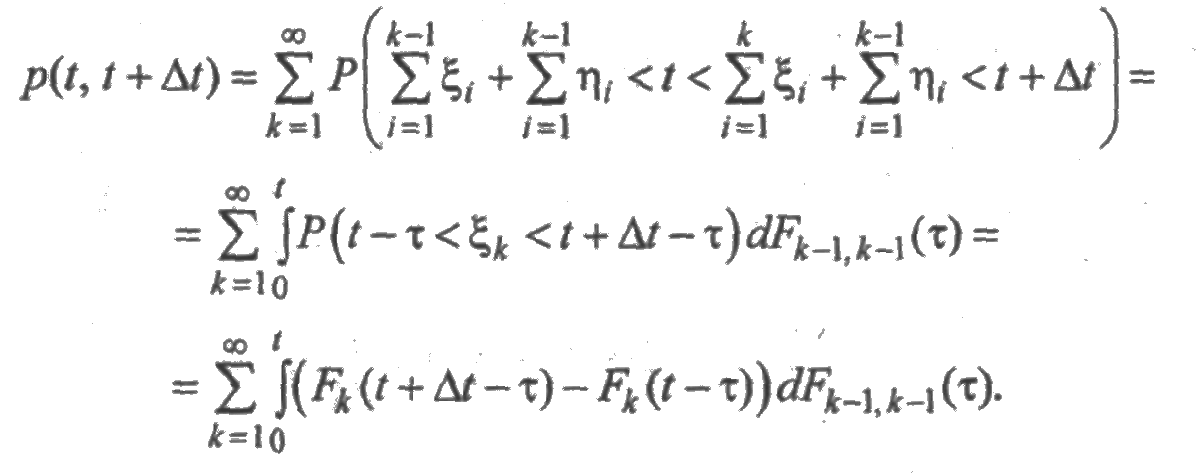
Используя (2.12), получим:

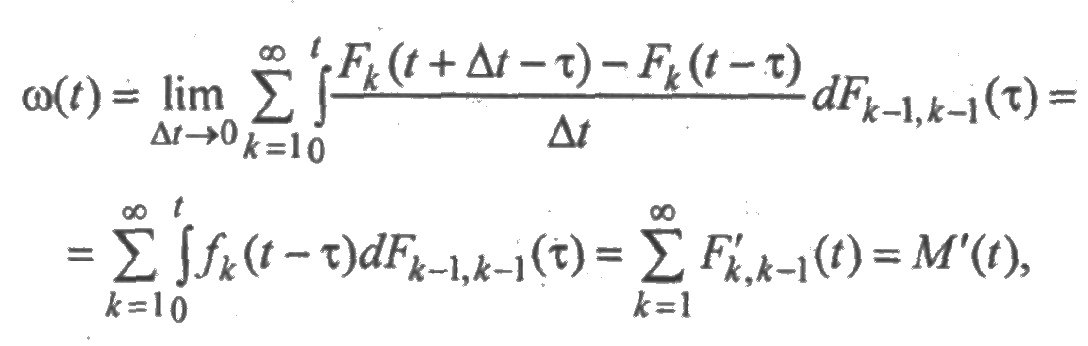
что и доказывает равносильность двух определений функции ω (t). Подобные рассуждения справедливы и для функции ω_B (t).

Из определения интенсивностей потоков отказов и восстановлений, а также из равенств (2.24) получаются следующие выражения для λ(t) и ω (t):

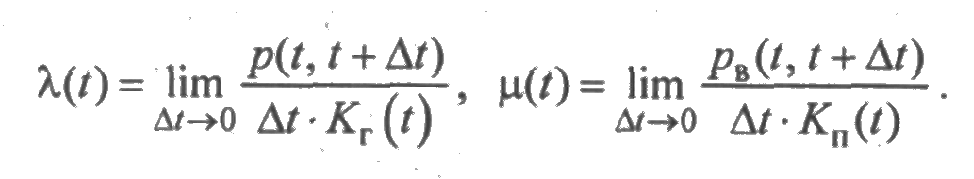
Из этих формул следует, что интенсивность потока отказов есть вероятность отказа за малый промежуток времени [ t, t+Δt ] при условии, что в момент t элемент находится в исправном состоянии, отнесенная к длине этого промежутка. Интенсивность потока восстановлений есть вероятность восстановления в течение времени [ t, t+Δt ] при условии, что в момент t элемент находится в состоянии восстановления, отнесенная к длине этого промежутка.

Перейдем к изучению случайных процессов χ(t) и χ_в(t). Рассмотрим случайный процесс χ(t), равный суммарному времени работы элемента в течение времени [0; t ]. Зафиксируем момент времени t ₀ и найдем закон распределения случайной величины χ(t₀).

Пусть F(t) — функция распределения случайной величины χ(t₀). Очевидно, что F(t) = 0 при t < 0 и F(t) =1 при t > t ₀. Из временной диаграммы, изображенной на рис. 2.8, следует, что при 0< t < t ₀

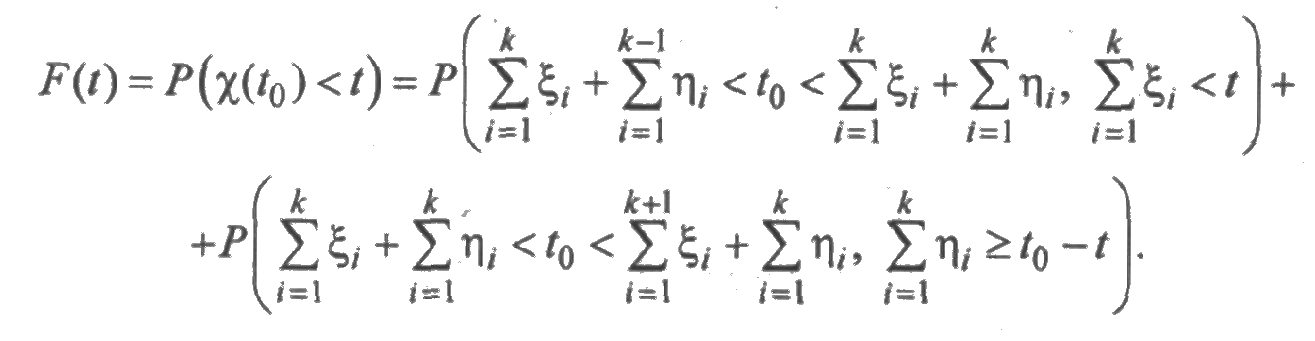
Из принятых ранее обозначений следует, что

Преобразуя эти выражения, получим

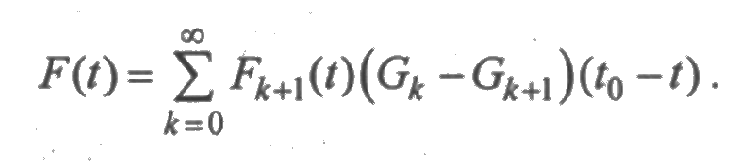
График функции F(t) представлен на рис. 2.9.

Функция F(t) имеет в точке t₀ разрыв, поскольку F(t₀ - 0) = F₁(t₀), и величина скачка равна 1 - F₁(t₀). Вычислим математическое ожидание случайной величины χ(t₀). Для случайной величины смешанного типа

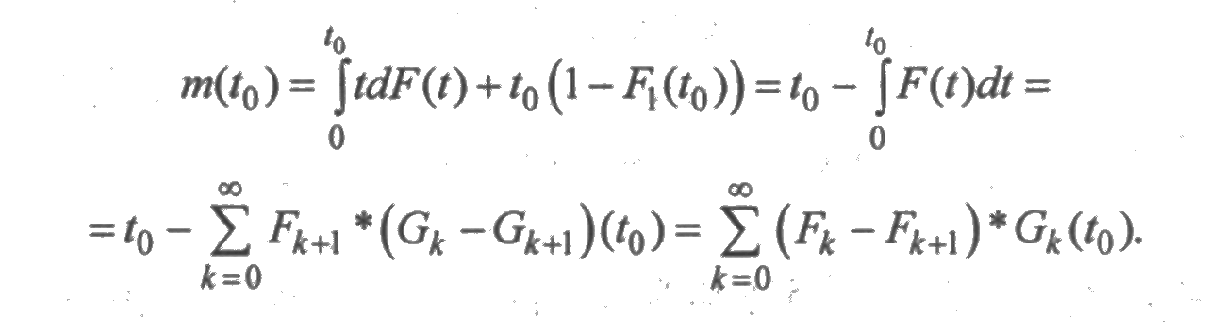
Таким образом, средняя суммарная наработка системы за время [ 0;t ] равна

Рассмотрим случайный процесс χ _в(t) равный суммарному времени восстановления элемента в течение времени [0; t ]. Можно показать, что при 0<t<t₀ закон распределения случайной величины χ _в(0) характеризуется функцией распределения

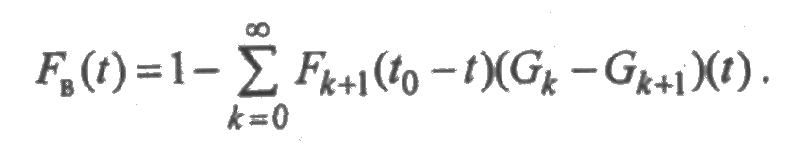
Полученная зависимость иллюстрируется графиком на рис. 2.10.

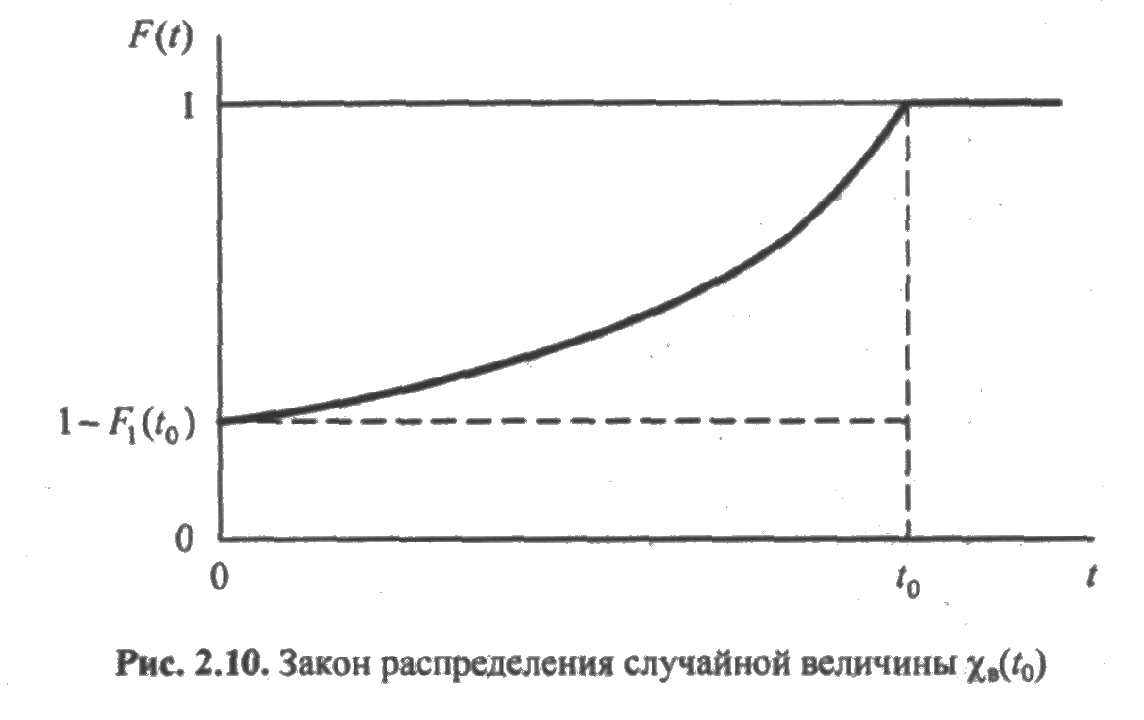
Математическое ожидание случайной величины χ _в(0) равно

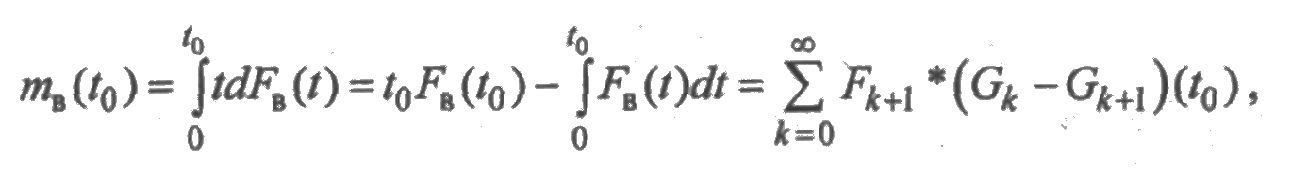
и, значит, среднее суммарное время восстановления элемента за время [0; t ] составляет

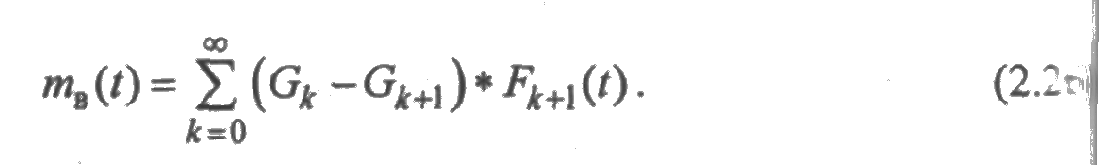
Складывая ряды (2.25) и (2.26), убеждаемся в том, что т(t) + m _в(t)= t. Вычислим функции готовности и простоя. Очевидно, что

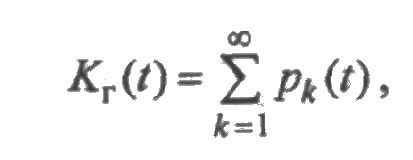
где р _к(0) - вероятность того, что момент времени t приходится на k-й интервал исправной работы элемента. Поскольку

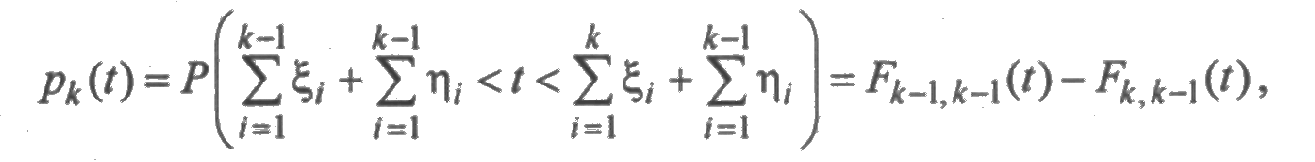
то

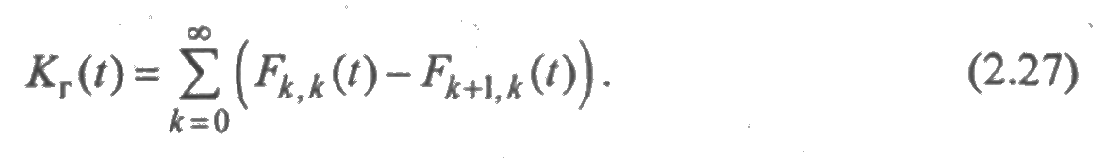
Таким же образом доказывается формула

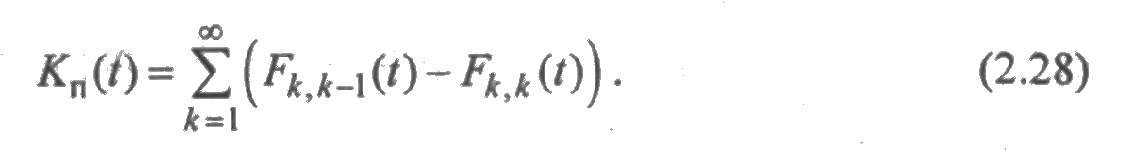
Дифференцируя функции т(t) и то, т_B(t) и сравнивая производные с выражениями (2.27) и (2.28), видим, что

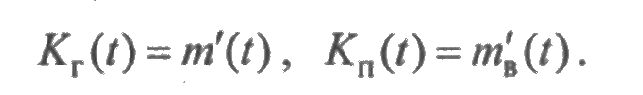
В частности, если законы распределения времени исправной работы на каждом интервале одинаковы и имеют плотность f(t), а законы распределения времени восстановления имеют плотность g(t), то соотношения для введенных характеристик можно записать в более компактном виде. Будем обозначать через f *^(k) k-кратную свертку функции f. Тогда из (2.23) получим сле­дующие выражения для параметров потоков:

откуда следуют зависимости

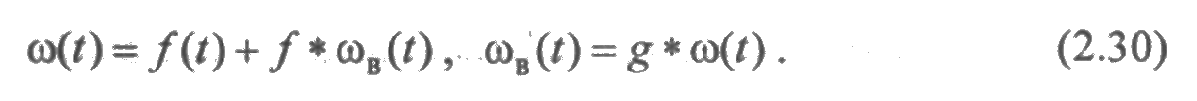
Для функций готовности и простоя из (2.27) и (2.28) будем иметь

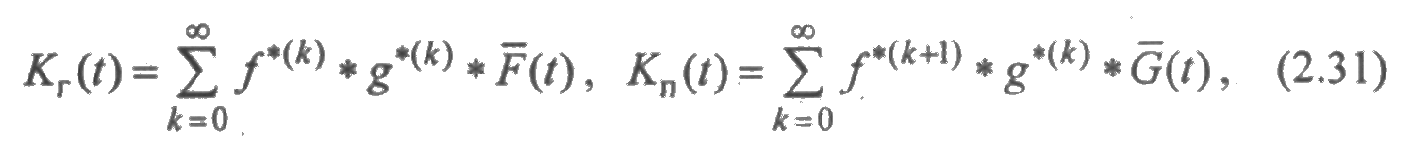
где

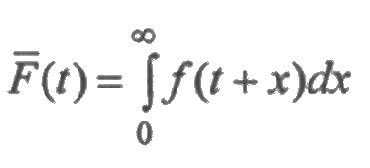
вероятность безотказной работы элемента в течение времени t, а

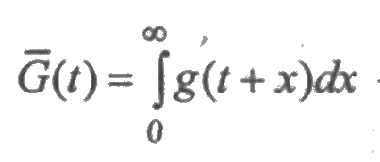
вероятность того, что за время t элемент не будет восстановлен.

Из (2.31) следует, что

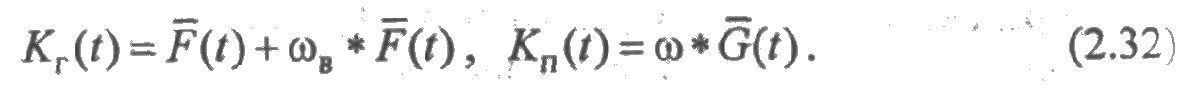
ПРИМЕР 2.6. Время до отказа элемента имеет нормальное распределение с параметрами α = 1000 час, s = 300 час. Время восстановления имеет нор­мальное распределение с параметрами b=10 час, r = 30 час. Требуется определить функцию готовности.

Решение. Вычислим функцию готовности по формуле (2.27). По свойству нормального распределения функции F_k,k(t) и F_k,k+1(t) также являются функциями нормального распределения с параметрами т_k = k(а + b ), и m_k + α, соответственно. Поэтому, используя функцию Лапласа, получим

Расчеты, выполненные по этой формуле, позволяют построить график функ­ции готовности (рис. 2.11).

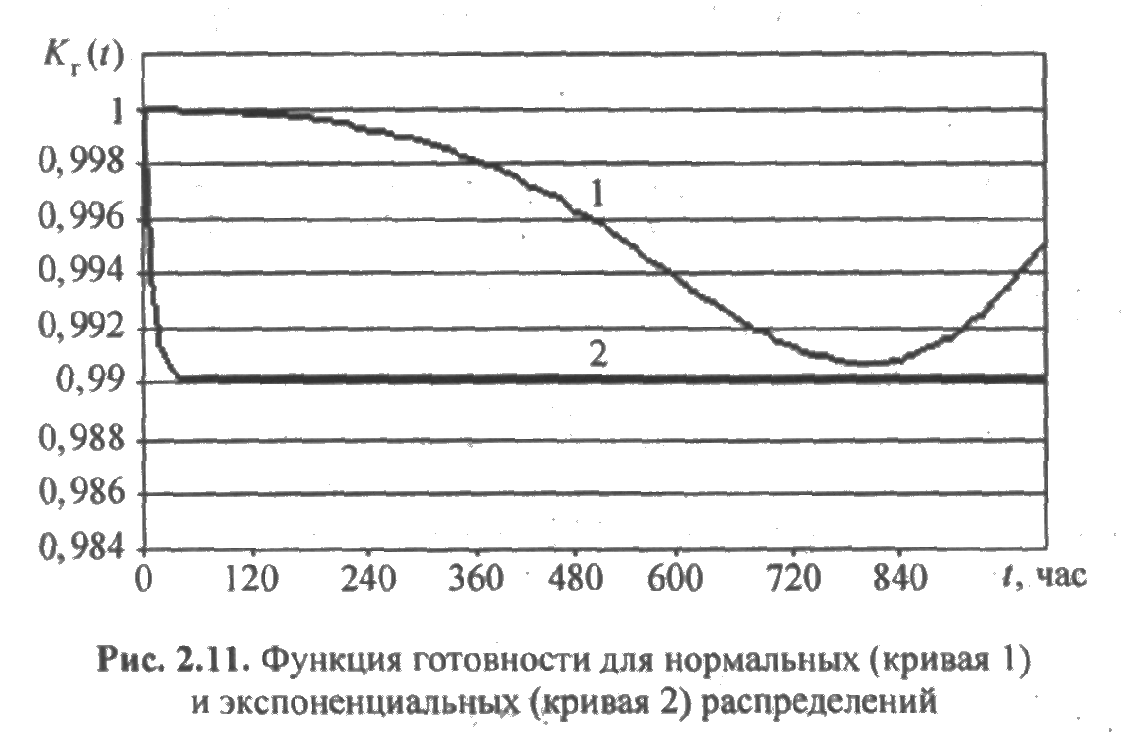
Для сравнения на этом же рисунке изображен график функции готовности, если время до отказа и время восстановления элемента имеют экспоненциальные распределения со средними а и b соответственно.

Различие двух кривых очевидно. Функция готовности для случая нормального распределения имеет колебательный характер, отсутствующий у системы с экспоненциальным законом распределения отказов и восстановлений. Стационарный режим в первом случае долго не наступает, во втором он наступает практически мгновенно.

2.6.2. Стационарные значения показателей надежности элемента

Получим предельные значения для показателей надежности восстанавливаемого элемента, предполагая, что с течением времени процесс функционирования элемента устанавливается и приобретает стационарный характер. Будем считать в дальнейшем, что f_k = f, g_k = g, k = 1, 2,... с математическими ожиданиями T и T _в соответственно.

Наиболее удобным способом вычисления предельных соотношений является представление характеристик в виде преобразования Лапласа.

Из равенств (2.29) следует, что параметры потоков отказов и восстановлений в изображениях имеют вид:

Следовательно, по свойствам (4) и (5) преобразования Лапласа (см. разд. 2.5) получим:

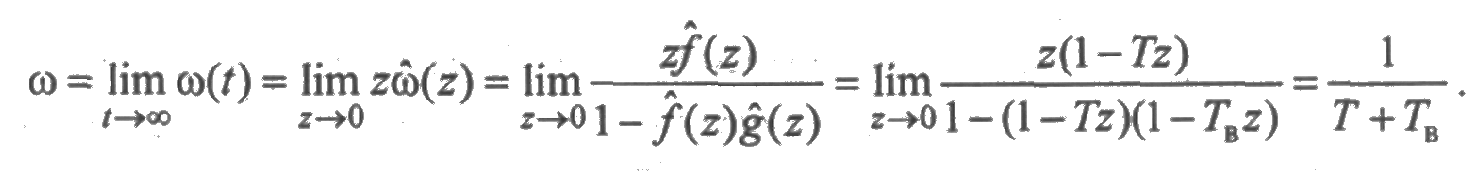
Аналогично

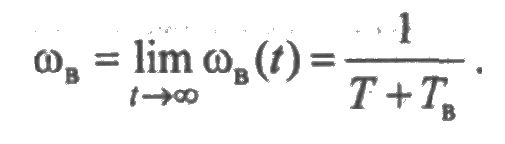
Таким образом, стационарные значения параметров потоков отказов и восстановлений одинаковы и равны

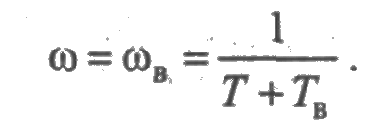
Из (2.32) следует, что

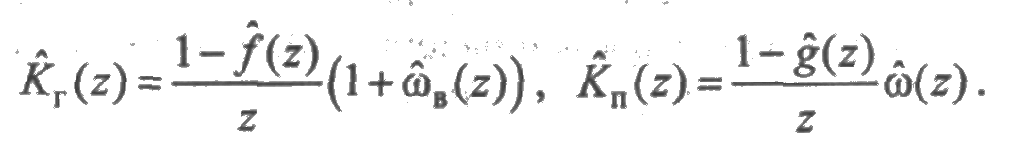
Следовательно, коэффициенты готовности и простоя равны соответственно

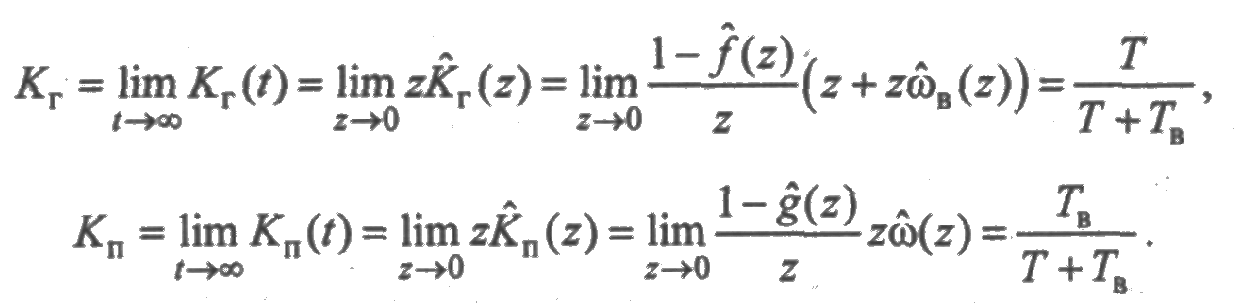
Коэффициент готовности определяется только средним временем работы элемента до отказа и средним временем восстановления вне зависимости от законов распределения. Это означает, что К_г нельзя применять для оценки надежности технических систем кратковременного использования. Более полная информация о работе такой системы содержится в функции готовности (см. рис. 2.11).

Получим предельные соотношения для среднего числа отказов и восстановлений. Вычислим предел разности при t→∞:

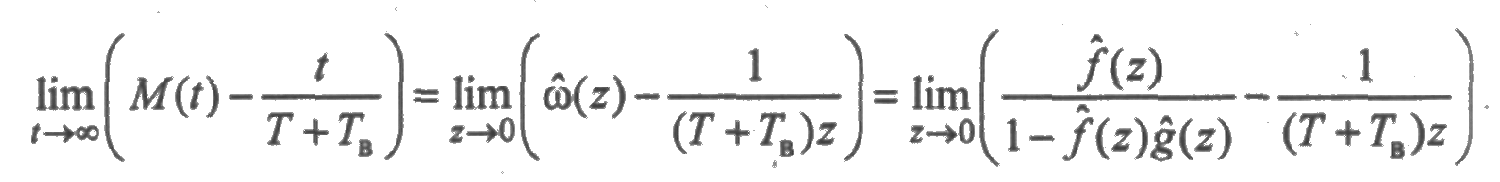
Применяя свойство (5) преобразования Лапласа, подучим

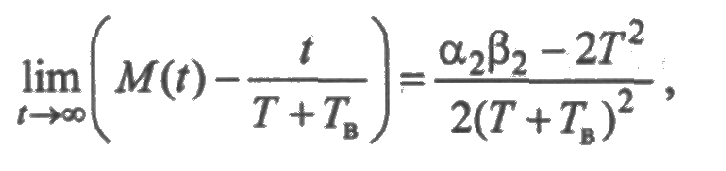
где α₂ и β₂ — вторые начальные моменты случайных величин с плотностями f(t) и g(t) соответственно. Отсюда следует асимптотическая оцени среднего суммарного числа отказов:

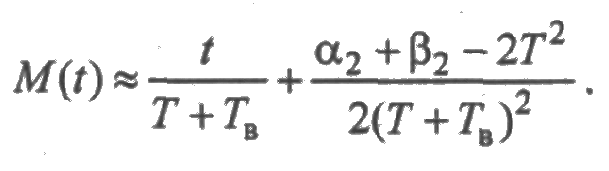
Аналогично при t→∞ имеет место асимптотическая оценка среднего суммарного числа восстановлений:

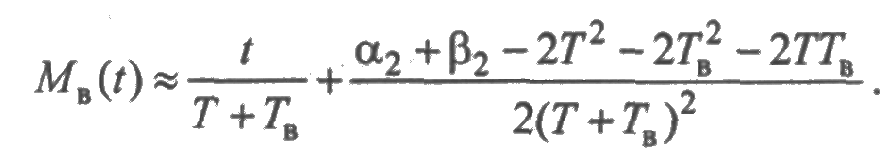
Похожие рассуждения позволяют найти асимптотические оценки для средней суммарной наработки и среднего суммарного времени восстановления элемента:

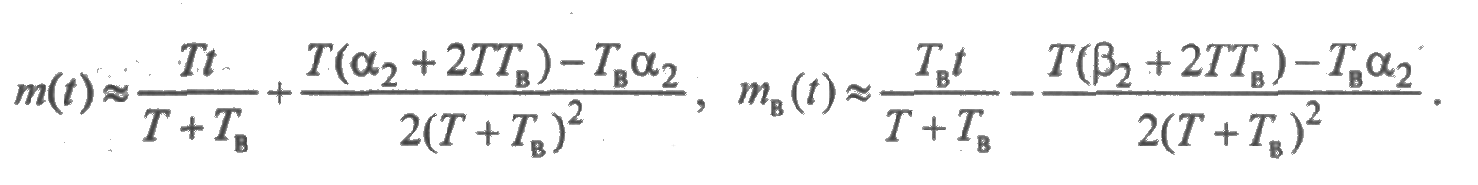
Теперь легко найти предельные соотношения для интенсивностей потоков отказов и восстановлений:

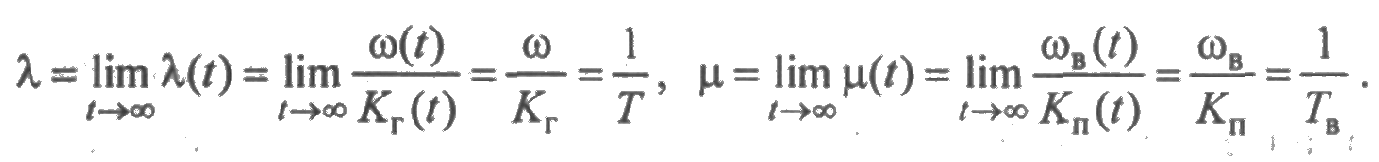
Вычислим стационарные значения средней наработки между отказами и среднего времени восстановления:

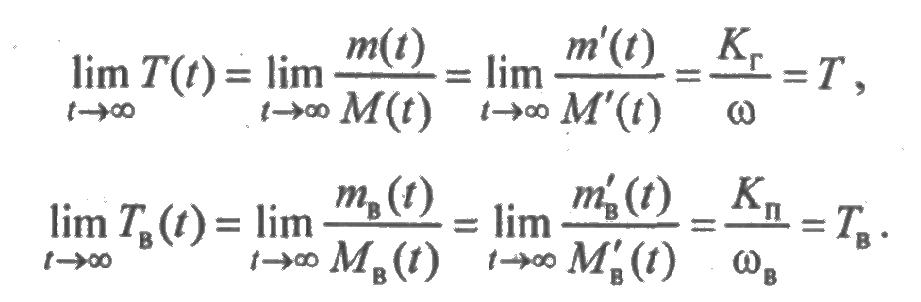
Как и следует ожидать, для стационарного режима средняя наработка между отказами равна среднему времени безотказной работы элемента.

2.6.3. Показатели надежности невосстанавливаемой и восстанавливаемой техники

В разд. 2.6.1 были введены показатели надежности элементов. Определим теперь показатели надежности системы. Пусть Е — множество состояний системы, k, l ϵ E — любые два состояния множества Е. Введем в рассмот­рение следующие случайные процессы и свяжем с ними определенные функции.

· ζ_k,l(t) — число переходов системы из состояния k в состояние l в течение времени [0;t], М_k,l(t) — математическое ожидание ζ_k,l(t), ω_k,l(t) = М’_k,l(t) — параметр перехода системы в момент времени t из состояния k в состояние l;

· χ_k(t) — суммарное время пребывания системы в состоянии k в течение времени [0;t], m_k(t) — математическое ожидание χ_k(t), p_k(t) = m’_k(t) — вероятность пребывания системы в момент времени t в состоянии k.

Определим теперь случайные процессы и некоторые производные от их функции для подмножеств состояний множества Е, где е и f — любые непересекающиеся подмножества множества состояний Е:

ζ_e,f(t) — число переходов системы из состояний множества е в состояния множества f в течение времени [0,t], M_e,f(t) — математическое ожидание ζ_e,f(t), ω_e,f(t) = М'_e,f(t) — параметр перехода в момент времени t из множества состояний е в множество состояний f;

χ_e(t) — суммарное время пребывания системы в состояниях множества e в течение времени [0;t], т_е(t) — математическое ожидание χ_e(t), p_e(t) = m’_e(t) — вероятность пребывания в момент времени t в каком-либо состоянии множества е.

Случайные процессы ζ_e,f(t) и χ_e(t) являются базовыми, поскольку через них может быть получена вся информация о работе системы с позиции теории надежности. Так, например, математические ожидания этих процессов позволяют определить среднее время Т_e,f(t)_е>/(1) пребывания системы в множестве е до перехода в множество f в течение времени [0;t]:

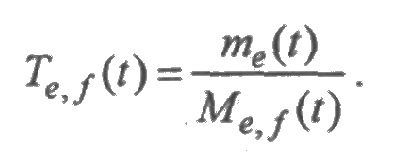
Интенсивность перехода системы в момент времени t из множества е в множество f определяется отношением:

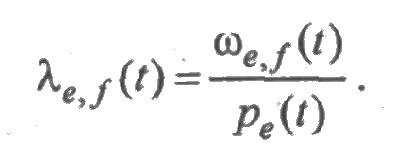
Укажем формулы связи между показателями, характеризующими множества состояний из Е и отдельные состояния множества Е:

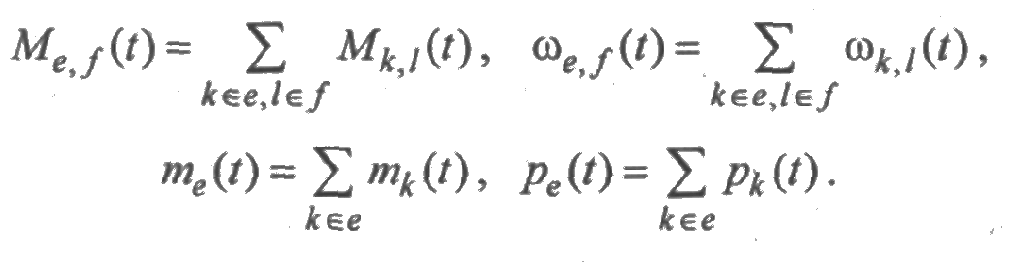
2.6.4. Основное уравнение функционирования системы

Предположим, что процесс функционирования системы состоит из случайных времен пребывания в некоторых состояниях и мгновенных переходов одного состояния в другое. Случайное время пребывания в состоянии i характеризуется вероятностью p_i(t), а переход из состояния i в состояние j характеризуется параметром перехода ω_i,j(t). Тогда имеет место система уравнений:

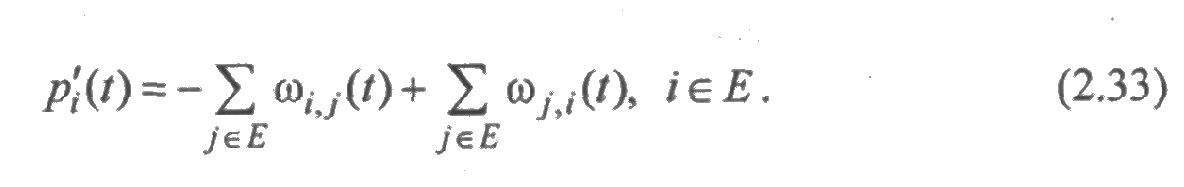
Для доказательства обозначим через число входов в состояние i из любого другого состояния, а через — число выходов из состояния i в любое другое состояние в течение времени [0; t ]. При фиксированном t это случайные величины, принимающие целочисленные значения. Рассмотрим 2 случая.

Случай 1. Состояние i не является начальным состоянием процесса функционирования.

Процесс не может выйти из состояния i, если он не оказался в этом состоянии, поэтому ≤ . После пребывания процесса в состоянии i в это состояние нельзя войти вновь до тех пор, пока процесс не выйдет из этого состояния, поэтому ≤ +1. Отсюда следует, что случайная величина - принимает только два значения: 0 или 1. При этом - = 1, если процесс пребывает в состоянии i. Вероятность этого события равна p_i(t). Аналогично - = 0, если процесс вышел из состояния i, но вновь еще не вошел в это состояние. Вероятность этого события равна 1- p_i(t). Следовательно, математическое ожидание случайной величины - равно p_i(t).

Так как

то

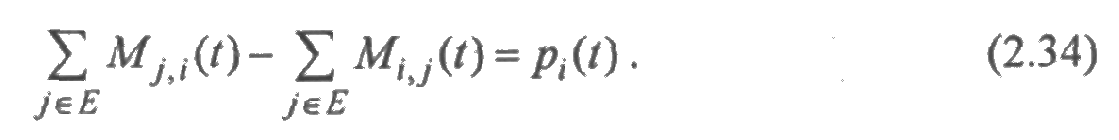
Случай 2. Состояние i является начальным состоянием процесса функционирования.

Очевидно, что здесь выполняется неравенство ≤ ≤ +1, поэтому случайная величина - может принимать только два значения 0 и 1 с вероятностями p_i(t) и 1 -p_i(t) соответственно.