
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Основные положения геометрической оптики
ГАУССОВА ОПТИКА (ЛУЧЕВАЯ ОПТИКА)
При рассмотрении дифракции Френеля, следует помнить, что соотношение только длины волны и линейного размера препятствия нацело не определяет условия возникновения дифракционной картины от точечного источника. Это ошибка. Необходимо еще учитывать третий параметр – это расстояние от источника до препятствия (или расстояние между препятствием и экраном, на котором наблюдается дифракционная картина). Так как степень приближения к геометрической оптике связана с тем, сколько зон Френеля уложилось на данном препятствии. Если линейные размеры препятствия того же порядка, что и размеры зоны Френеля (например, 1-ой)
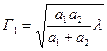 (1)
(1)
(Если размеры препятствия много больше длины волны – геометрическая оптика).
то, по-видимому, проявятся волновые свойства излучения. Тогда можно ввести так называемый параметр дифракции 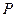 .
.
 (2)
(2)
где  ,
, 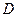 – размер препятствия.
– размер препятствия.
Следовательно, три величины 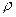 ,
,  и
и 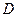 определяют условия дифракции и соотношение между ними оказываются решающими при переходе от волновой оптики к геометрической.
определяют условия дифракции и соотношение между ними оказываются решающими при переходе от волновой оптики к геометрической.
Если
 ,
,
то  – щель (препятствие) широкая;
– щель (препятствие) широкая;
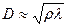 , (3)
, (3)
то есть 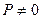 – щель узкая, и учёт волновых свойств должен играть основную роль, а при
– щель узкая, и учёт волновых свойств должен играть основную роль, а при  следует говорить о соблюдении законов геометрической оптики.
следует говорить о соблюдении законов геометрической оптики.
Итак,
1. при
 всегда
всегда  , (4)
, (4)
следовательно  можно считать основным условием перехода от волновой оптики к геометрической, так как при любых конечных расстояниях параметр дифракции всегда мал
можно считать основным условием перехода от волновой оптики к геометрической, так как при любых конечных расстояниях параметр дифракции всегда мал 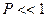 (волновые эффекты трудно обнаружить);
(волновые эффекты трудно обнаружить);
2. если  велико, то при достаточно малых
велико, то при достаточно малых 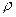 также
также
 и
и  , (5)
, (5)
то есть при малых расстояниях реализуются условия геометрической оптики, а по мере увеличения 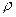 необходимо все в большей степени учитывать явления дифракции.
необходимо все в большей степени учитывать явления дифракции.
Таким образом рассмотренные нами условия перехода от волновой оптики к геометрической ( ) являются прямым следствием основных положений классической теории дифракции.
) являются прямым следствием основных положений классической теории дифракции.
Покажем, что уравнения электромагнитной теории света содержат в себе решения для описания построений геометрической оптики, оперирующей понятием лучей, которые в оптически однородной среде прямолинейны.
Рассмотрим плоскую электромагнитную волну, то есть направление ( ) её распространения и амплитуда повсюду одинакова (по крайней мере на протяжении расстояния порядка
) её распространения и амплитуда повсюду одинакова (по крайней мере на протяжении расстояния порядка  ). В плоской волне волновые поверхности представляют собой плоскости, перпендикулярные направлению распространения (лучу). На бесконечно малом участке любая волна эквивалентна плоской.
). В плоской волне волновые поверхности представляют собой плоскости, перпендикулярные направлению распространения (лучу). На бесконечно малом участке любая волна эквивалентна плоской.
В плоской монохроматической волне электромагнитное поле описывается уравнением:
 , (6)
, (6)
где  ,
,  (7)
(7)
 ,
,  (8)
(8)
Введем функцию  , называемую эйконалом. Она конечная и непрерывная в данной области пространства. Определим функцию
, называемую эйконалом. Она конечная и непрерывная в данной области пространства. Определим функцию  , записав
, записав
 . (9)
. (9)
На малых участках пространства разложим  в ряд и сохраним члены первого порядка:
в ряд и сохраним члены первого порядка:
 . (10)
. (10)
Выберем начало координат внутри рассматриваемого участка пространства и значения 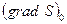 и функции
и функции 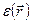 возьмем в начале координат. Тогда амплитуда любой электромагнитной волны:
возьмем в начале координат. Тогда амплитуда любой электромагнитной волны:
 , (11)
, (11)
где  .
.
Сравнивая уравнения (11) и (7), получаем
 (12)
(12)
или 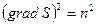 – уравнение эйконала.
– уравнение эйконала.
Из уравнения (12) следует, что единичный вектор луча  можно найти из:
можно найти из:
 . (13)
. (13)
Из уравнения (12) следует, что если  , то в такой оптически однородной среде лучи будут прямолинейны. И решением уравнения (12) будет линейная функция
, то в такой оптически однородной среде лучи будут прямолинейны. И решением уравнения (12) будет линейная функция
 , (14)
, (14)
где 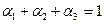 и
и 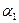 ,
,  ,
,  называются направляющими косинусами.
называются направляющими косинусами.
Решением уравнения (12) с двумя произвольными постоянными, то есть получено уравнение плоскости. Это означает, что семейство нормалей в данном случае является системой параллельных лучей.
Решением уравнения (12) с одной особой точкой (при  ) является
) является
 , где
, где  (15)
(15)
и 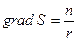 .
.
Следовательно, и семейство нормалей представляет собой систему лучей, расходящихся из точки  , ортогональных поверхностям равной фазы сферической волны.
, ортогональных поверхностям равной фазы сферической волны.
 Уравнение (12) позволяет определить, как искривляются световые лучи в оптически неоднородной среде (Рис.1).
Уравнение (12) позволяет определить, как искривляются световые лучи в оптически неоднородной среде (Рис.1).
Приращение дуги луча обозначаем через  , тогда
, тогда
 ,
,
а уравнение луча
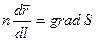 . (16)
. (16)
Рис.1 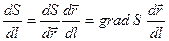 , (17)
, (17)
Затем умножим уравнение (17) на  , тогда получаем уравнение
, тогда получаем уравнение
 ,
,
Следовательно
 (18)
(18)
Из уравнения (18) следует, что в оптически однородной среде лучи света есть семейство прямых линий.
Продифференцируем уравнение (12) по  , уравнения луча
, уравнения луча

 , где
, где 
Тогда
 , (19)
, (19)
 ,
,
где  – единичный вектор нормали к лучу,
– единичный вектор нормали к лучу,  – радиус кривизны.
– радиус кривизны.
Умножив уравнение (19) на  окончательно получаем
окончательно получаем
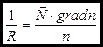 или
или  (20)
(20)
 Уравнение (20) показывает, что луч изгибается в сторону увеличения показателя преломления и кривизна луча будет возрастать с увеличением градиента показателя преломления, то есть с увеличением оптической неоднородности среды. Если известна функция
Уравнение (20) показывает, что луч изгибается в сторону увеличения показателя преломления и кривизна луча будет возрастать с увеличением градиента показателя преломления, то есть с увеличением оптической неоднородности среды. Если известна функция  можно вычислить кривизну лучей.
можно вычислить кривизну лучей.
Пример:  . Тогда искривление луча будет описываться цепной функцией, которая при небольших
. Тогда искривление луча будет описываться цепной функцией, которая при небольших 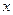 хорошо аппроксимируется параболой
хорошо аппроксимируется параболой  .
.
 В рамках такого приближения можно описать явление миража. Раскаленная Земля создает неоднородность прилегающих слоев воздуха, плотность которого
В рамках такого приближения можно описать явление миража. Раскаленная Земля создает неоднородность прилегающих слоев воздуха, плотность которого 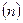 возрастает с увеличением расстояния от поверхности Земли, что в свою очередь приводит к искривлению лучей.
возрастает с увеличением расстояния от поверхности Земли, что в свою очередь приводит к искривлению лучей.
Аналогично для лучей заходящего Солнца (Рис.2). В данном случае  показатель
показатель
Рис.2 преломления убывает при увеличении высоты. В верхних слоях атмосферы показатель преломления меньше чем в нижних слоях. За счет искривления луча, Солнце будет казаться выше, чем есть на самом деле.
Для обоснования геометрической оптики используют принцип Ферма или принцип наикратчайшего оптического пути (или наименьшего времени). Покажем это:
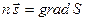 , (21)
, (21)
проинтегрируем
 ,
,
то есть окончательный вариант не зависит от формы пути интегрирования от  к
к  и равен разности значений эйконала в точках
и равен разности значений эйконала в точках  и
и  . Уравнение (21) называется интегральным инвариантом Лагранжа.
. Уравнение (21) называется интегральным инвариантом Лагранжа.
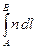 – оптическая длина некоторой кривой (22)
– оптическая длина некоторой кривой (22)
так как из свойств скалярного произведения
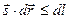
следует
 . (23)
. (23)
Из выражения (23) следует, что интегралы равны, если  и
и  совпадают в любой точке рассматриваемой кривой, то есть если кривая является реальным лучом. Принцип Ферма: оптическая длина реального луча между любыми двумя точками
совпадают в любой точке рассматриваемой кривой, то есть если кривая является реальным лучом. Принцип Ферма: оптическая длина реального луча между любыми двумя точками  и
и  короче оптической длины любой другой кривой, соединяющей эти точки.
короче оптической длины любой другой кривой, соединяющей эти точки.
Поскольку  , то
, то
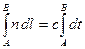 .
.
Оптическая длина кривой между точками  и
и  пропорциональна времени, требующемуся свету для прохождения вдоль этой кривой. Это есть принцип наименьшего времени, то есть свет выбирает из всех возможных путей, соединяющих две точки, тот путь, который требует наименьшего времени для его прохождения.
пропорциональна времени, требующемуся свету для прохождения вдоль этой кривой. Это есть принцип наименьшего времени, то есть свет выбирает из всех возможных путей, соединяющих две точки, тот путь, который требует наименьшего времени для его прохождения.
Если первая вариация равна нулю
 , то
, то 
имеет стационарное значение – это основное отличие реального луча, от остальных кривых (отраженных от зеркал) соединяющих две точки.
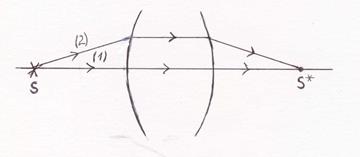

Эллиптическое зеркало Сумма длин луча 1 = сумме длин луча 2
Date: 2016-07-25; view: 284; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |