Статистические оценки параметров распределения

Федеральное агентство по образованию

Воронежский государственный университет

Mатематическая статистика

Учебно-методическое пособие

по специальности 071900 «Информационные системы и технологии»

Для студентов 2 курса очной формы обучения

Воронеж – 2011

Оглавление

1. Основные понятия…………………………………………………………………………2

2. Статистические оценки параметров распределения…………………………………….5

3. Метод моментов …………………………………………………………………………...6

4. Метод максимального правдоподобия……………………………………………………8

5. Интервальные оценки…………………………………………………………………….10

6. Вероятностные распределения, применяемые в статистике: гамма-распределение, распределение 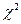, распределение Стьюдента………………………………………….12

7. Критерий согласия 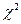…………………………………………………………………….16

Основные понятия

СПРАВОЧНЫЕ СВЕДЕНИЯ

1.1 Предмет, задачи математической статистики. Основные понятия

Предмет. Математической статистикой называется наука, занимающаяся методами обработки опытных данных, полученных в результате наблюдений над случайными явлениями.

Задачи. Упорядочение статистического материала, представление его в наиболее удобном для обозрения и анализа виде. Оценка вероятностных характеристик случайной величины, над которой велись наблюдения, а также проверка вероятностных гипотез.

Статистическое распределение выборки. Статистическим распределением выборки называют перечень наблюдавшихся значений признака 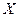, записанных в возрастающем порядке, и соответствующих им частот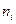

(сумма всех частот равна объему выборки 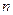) или относительных частот (в качестве частоты интервала принимают сумму частот наблюдавшихся значений, попавших в этот интервал).

Эмпирическая функция распределения. Эмпирической функцией распределения называют функцию , определяющую для каждого значения 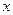относительную частоту события

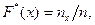
где - число наблюдавшихся значений, меньших 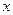, 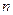-объем выборки.

Эмпирическая функция распределения обладает следующими свойствами:

1. Значения эмпирической функции распределения принадлежат отрезку .
2. Эмпирическая функция распределения является неубывающей функцией.
3. Эмпирическая функция распределения равна нулю левее наименьшего наблюденного значения и единицы – правее наибольшего.

Гистограмма. Гистограммой частот (статистический аналог кривой распределения) называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длины , а высоты равны отношению (плотность частоты). Площадь частичного 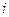-го прямоугольника равна - сумме частот вариант, попавших в 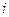-й интервал. Площадь гистограммы частот равна сумме всех частот, т.е. объему выборки .

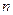Гистограммой относительных частот называют ступенчатую функцию, состоящую из прямоугольников, основаниями которых служат частичные интервалы длины , а высоты равны отношению (плотность относительной частоты), где - относительная частота, соответствующая 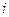-му наблюденному значению. Площадь частичного 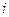-го прямоугольника равна -относительной частоте наблюдавшихся значений, попавших в 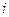-й интервал. Площадь гистограммы относительных частот равна единице.

Примеры с решениями

Пример 1. Выборка задана в виде распределения частот:

Найти распределение относительных частот.

Решение. Найдем объем выборки: Найдем относительные частоты:

Напишем распределение относительных частот:

Проверка: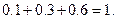

Пример 2. Найти эмпирическую функцию распределения по заданному распределению выборки:

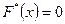Решение. Найдем объем выборки: Наименьшее наблюденное значение равно единице, следовательно, при

Значение а именно наблюдалось 10 раз, поэтому при Значения а именно: наблюдались раз, следовательно, при Так как - наибольшее наблюденное значение, то при

Таким образом, искомая эмпирическая функция распределения имеет вид

График функции изображен на рисунке 1.

Рис.1

Пример 3. Построить гистограмму частот по данному распределению выборки объема :

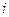
Номер интервала	Частичный интервал	Сумма частот наблюдавшихся значений интервала	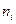Плотность частоты
	1-5		2.5
	5-9
	9-13		12.5
	13-17
	17-21

Решение. Построим на оси абсцисс заданные интервалы длины . Проведем над этими интервалами отрезки, параллельные оси абсцисс и находящиеся от нее на расстояниях, равных соответствующим плотностям частоты . Например, над интервалом построим отрезок, параллельный оси абсцисс, на расстоянии ; аналогично строят остальные отрезки. Гистограмма частот изображена на рисунке 2.

Рис. 2

Задачи

Задача 1. Выборка задана в виде распределения частот:

Найти распределение относительных частот.

Задача 2. Построить гистограмму частот по данному распределению выборки:

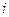
Номер интервала	Частичный интервал	Сумма частот наблюдавшихся значений интервала	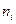Плотность частоты
	2-7
	7-12
	12-17
	17-22
	22-27

Задача 3. Построить гистограмму относительных частот по данному распределению выборки:

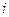
Номер интервала	Частичный интервал	Сумма частот наблюдавшихся значений частичного интервала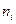
	2-5
	5-8
	8-11
	11-14

Статистические оценки параметров распределения

Статистической оценкой 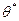неизвестного параметра 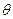теоретического распределения называют функцию от наблюдаемых случайных величин .

Точечной называют статистическую оценку, которая определяется одним числом , где ­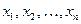- результаты 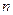наблюдений над количественным признаком 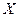(выборка).

Несмещенной называют точечную оценку, математическое ожидание которой равно оцениваемому параметру при любом объеме выборки:

Эффективной называют точечную оценку, обладающей минимальной дисперсией:

Состоятельной называют точечную оценку, которая при увеличении числа опытов 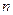приближается (сходится по вероятности) к искомому параметру:

Естественной оценкой для математического ожидания 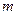случайной величины 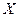является среднее арифметическое ее наблюденных значений (или статистическое среднее):

Эта оценка является состоятельной, эффективной и несмещенной.

Оценка

Является состоятельной и несмещенной для дисперсии .

Примеры с решениями

Пример 1. По данному распределению выборки объема 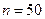найти несмещенную оценку математического ожидания.

наблюдаемые значения
частота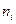

Решение. Несмещенной оценкой математического ожидания является статистическое среднее

Пример 2. По распределению выборки из предыдущего примера найти несмещенную оценку для дисперсии.

Решение. Несмещенной оценкой для дисперсии является оценка

В качестве статистического среднего 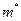использовали значение, полученное в предыдущем примере.

Задачи

Задача 1. Из генеральной совокупности извлечена выборка объема

наблюдаемые значения
частота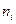

Найти несмещенную оценку генеральной средней.

Метод моментов

Метод моментов точечной оценки неизвестных параметров заданного распределения состоит в приравнивании теоретических моментов соответствующим эмпирическим моментам того же порядка.

Если распределение определяется одним параметром, то для его отыскания приравнивают один теоретический момент одному эмпирическому моменту того же порядка. Например, можно приравнять начальный теоретический момент первого порядка начальному эмпирическому моменту первого порядка:

. (1)

Математическое ожидание является функцией от неизвестного параметра заданного распределения, поэтому, решив уравнение (1) относительно неизвестного параметра, получим его точечную оценку.

Если распределение определяется двумя параметрами, то приравнивают два теоретических момента двум соответствующим эмпирическим моментам того же порядка.

Например,

(2)

Левые части этих равенств являются функциями от неизвестных параметров, поэтому, решив систему (2) относительно неизвестных параметров, получим их точечные оценки.

Примеры с решениями

Пример 1. Случайная величина 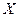распределена по закону Пуассона

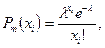
где 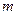-число испытаний, произведенных в одном опыте, - число появлений события в 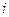-м опыте. Найти методом моментов по выборке 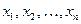точечную оценку неизвестного параметра 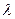, определяющего распределение Пуассона.

Решение. Требуется оценить один параметр, поэтому достаточно иметь одно уравнение относительно этого параметра. Приравниваем начальный теоретический момент первого порядка начальному эмпирическому моменту первого порядка :

Приняв во внимание, что получим Учитывая, что математическое ожидание распределения Пуассона равно параметру 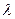этого распределения, имеем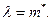

Таким образом, точечной оценкой параметра 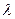распределения Пуассона служит выборочная средняя:

Пример 2. Найти методом моментов по выборке 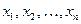точечные оценки неизвестных параметров 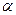и гамма-распределения, плотность которого

.

Решение. Для отыскания двух неизвестных параметров необходимо иметь два уравнения; приравняем начальный теоретический момент первого порядка начальному эмпирическому моменту первого порядка и центральный теоретический момент второго порядка центральному эмпирическому моменту второго порядка

Учитывая, что имеем

Математическое ожидание и дисперсия гамма-распределения соответственно равны следовательно

Решив эту систему, получим искомые точечные оценки неизвестных параметров:

Пример 3. Случайная величина 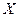имеет геометрическое распределение:

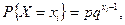
где - число испытаний, произведенных до появления события, 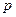- вероятность появления события в одном испытании, 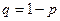. Найти методом моментов точечную оценку параметра .

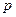Решение. Для геометрического распределения имеем следующий ряд распределения

Учитывая, что , получаем

Таким образом, следовательно

.

Задачи

Задача 1. Найти методом моментов по выборке 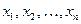точечные оценки неизвестных параметров 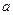и 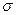нормального распределения, плотность которого

Задача 2. Устройство состоит из элементов, время безотказной работы которых подчинено гамма-распределению. Испытания пяти элементов дали следующие наработки (время работы элемента в часах до отказа): 50, 75, 125, 250, 300. Найти методом моментов точечные оценки неизвестных параметров 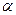и , которыми определяется гамма-распределение.

Задача 3. Случайная величина 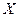(число нестандартных изделий в партии) распределена по закону Пуассона. Ниже приведено распределение нестандартных изделий в партиях (в первой строке указано количество нестандартных изделий в одной партии, во второй строке указана частота 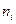- число партий, содержащих нестандартных изделий):

Найти методом моментов точечную оценку неизвестного параметра 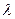распределения Пуассона.

Задача 4. Найти методом моментов по выборке 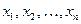точечную оценку неизвестного параметра 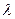показательного распределения, плотность которого

Date: 2016-07-25; view: 1887; Нарушение авторских прав