Эквивалентные преобразования электрических цепей

Последовательное соединение - это совокупность связанных элементов электрической цепи, не имеющая узлов.

Отсюда следует, что по всем элементам последовательного соединения протекает одинаковый ток, т.к. изменение тока может происходить только в узлах электрической цепи.

В последовательное соединение в общем случае может входить любое количество резисторов и источников ЭДС (рис. 1), но не может входить более одного источника тока, т.к. это противоречило бы свойству каждого из источников создавать в цепи ток не зависящий от внешних элементов.

Падение напряжения между точками a и b рис. 1 можно представить разностью потенциалов этих точек U_ab = j _a - j _b. Формально в эту разность можно включить произвольное число значений потенциалов (например, потенциалов точек соединения элементов) с противоположными знаками, а затем попарно объединить их.

Таким образом, любое последовательное соединение можно преобразовать к последовательному соединению одного эквивалентного резистора и одного источника ЭДС. Причем, сопротивление эквивалентного резистора равно сумме всех сопротивлений входящих в соединение, а ЭДС эквивалентного источника равна алгебраической сумме ЭДС источников входящих в соединение.

Последовательное соединение элементов обладает свойством коммутативности, т.е. любые элементы этого соединения могут произвольно переставляться в пределах соединения. Это свойство непосредственно следует из коммутативности слагаемых выражений (1).

Так как эквивалентное сопротивление R представляет собой сумму положительных слагаемых, то R > r_max, где r_max - наибольшее из сопротивлений, входящих в соединение.

Если последовательное соединение подключено к узлам электрической цепи, то его определение тождественно определению ветви, следовательно, ветвь может быть образована только последовательным соединением.

ЗАДАЧА 1

В отличие от последовательного соединения, в параллельном следует различать параллельное соединение элементов цепи и параллельное соединение ветвей.

Параллельное соединение элементов - это совокупность элементов электрической цепи, объединенных двумя узлами и не имеющих связей с другими узлами.

В параллельное соединение элементов в общем случае могут входить резисторы и
источники тока (рис. 2), но не может входить более одного источника ЭДС, т.к. это противоречило бы их свойству создавать на выходе разность потенциалов не зависящую от внешней цепи.

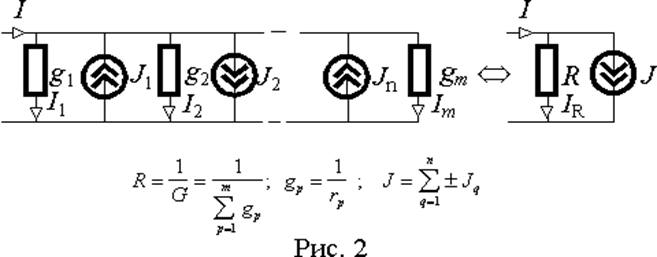Все элементы в параллельном соединении подключены к двум узлам и падение напряжения между этими узлами одинаково для всех элементов.

Общий ток, протекающий через параллельное соединение I можно представить суммой токов в отдельных элементах в виде I = I ₁+ I ₂+...+ I_n - J ₁+ J ₂+...+ J_m. Отсюда, раскрывая токи через сопротивления через напряжение между узлами U, получим

Таким образом, параллельное соединение любого количества элементов можно преобразовать к параллельному соединению одного эквивалентного резистора и одного источника тока. Причем, сопротивление эквивалентного резистора равно величине обратной сумме всех проводимостей резисторов входящих в соединение, а ток эквивалентного источника равен алгебраической сумме токов источников входящих в соединение.

Аналогично последовательному соединению, параллельное обладает свойством коммутативности, вытекающим из свойства коммутативности сумм выражений (2).

При параллельном соединении для эквивалентной проводимости G, являющейся суммой проводимостей отдельных элементов, справедливо отношение G > g_max, где g_max - наибольшая из проводимостей элементов, образующих соединение. Отсюда G =1/ R > g_max =1/ r_min Þ R < r_min, т.е. эквивалентное сопротивление резисторов, входящих в параллельное соединение меньше наименьшего из них r_min.

Понятие сопротивления более привычно и употребимо, чем эквивалентное ему понятие проводимости. Поэтому при параллельном соединении приходится решать задачу определения именно эквивалентного сопротивления. Для двух, трех и четырех соединенных параллельно резисторов эквивалентные сопротивления R приведены в таблице 1. Для большего числа сопротивлений нетрудно получить аналогичные выражения из соотношений, приведенных на рис. 2.

Таблица 1.

	r 1; r 2	r 1; r 2; r 3	r 1; r 2; r 3 ; r 4
R =

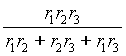
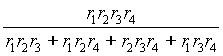
ЗАДАЧА 2

В параллельное соединение могут входить не только элементы, но и ветви, каждая из которых может быть последовательным соединением элементов (рис. 3 а)). В этом случае используется понятие параллельного соединения ветвей, под которым понимают совокупность ветвей электрической цепи, объединенных двумя узлами и не имеющих связей с другими узлами.

На рис. 3 а) ветви R₁R₂ и R₃ соединены параллельно, но элементы R₁R₃ и R₂R₃ параллельного соединения не образуют, т.к. эти пары элементов не объединены двумя узлами. Очевидно, что для них не выполняется и условие равенства падений напряжения.

ЗАДАЧА 3

Схемы цепей рис. 3 относят обычно к смешанному соединению, понимая под ним совокупность последовательного и параллельного соединений элементов и ветвей цепи.

Можно показать, что любую электрическую цепь путем поэтапных преобразований соединений элементов можно привести к последовательному соединению R-E или эквивалентному параллельному соединению G - J. Этот метод позволяет решать довольно сложные задачи и особенно эффективен, если требуется определить режим в какой-либо отдельной ветви цепи. Пример таких преобразований приведен на рис. 4.

Здесь на отдельных этапах преобразования параметры элементов определяются из выражений: R ₃₄= R ₃+ R ₄; J ₂= E ₂/ R ₂; R ₂₃₄=(R ₂ R ₃₄)/(R ₂+ R ₃₄); J ' = J + J ₂; E ' = J ' R ₂₃₄; R = R ₁+ R ₂₃₄; E = E ' - E ₁; J = E / R.

Особая задача, связанная с преобразованием цепей, состоит в определении сопротивления ( входного сопротивления ) цепи относительно точек разрыва. Она возникает, в частности, при использовании метода эквивалентного генератора для анализа электрических цепей в статических режимах, а также при составлении характеристического уравнения для анализа переходных процессов. Можно показать, что эквивалентное сопротивление R на рис. 4, является входным сопротивлением этой цепи и может быть определено по описанной ниже методике.

Собственно, методика заключается в том, что до начала эквивалентных преобразований в цепи нужно заменить все источники ЭДС и тока их эквивалентными сопротивлениями, а затем определить эквивалентное сопротивление. Как известно, сопротивление источника ЭДС равно нулю, а сопротивление источника тока - бесконечности. Поэтому на электрической схеме источники ЭДС нужно заменить связью, а источники тока - разрывом цепи. Рассмотрим этот процесс на примере рис. 5, где точка разрыва цепи, относительно которой нужно определить входное сопротивление, помечена крестиком.

Вначале заменим источники их эквивалентными сопротивлениями и изобразим разрыв в явном виде точками a и b (рис. 5 б)). Теперь задача становится очевидной, т.к. цепь от точки a к точке b представляет собой последовательное соединение R ₁ и R ₃.

ЗАДАЧА 4

2.1 Последовательное соединение элементов электрических цепей

На рис. 2.1 изображена электрическая цепь с последовательно соединенными сопротивлениями.

Рис. 2.1

Напряжение на зажимах источника ЭДС равно величине электродвижущей силы. Поэтому часто источник на схеме не изображают.
Падения напряжений на сопротивлениях определяются по формулам

В соответствии со вторым законом Кирхгофа, напряжение на входе электрической цепи равно сумме падений напряжений на сопротивлениях цепи.

где - эквивалентное сопротивление.

Эквивалентное сопротивление электрической цепи, состоящей из n последовательно включенных элементов, равно сумме сопротивлений этих элементов.

2.2. Параллельное соединение элементов
электрических цепей

На рис. 2.2 показана электрическая цепь с параллельным соединением сопротивлений.

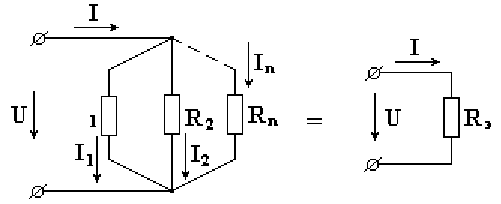
Рис. 2.2

Токи в параллельных ветвях определяются по формулам:

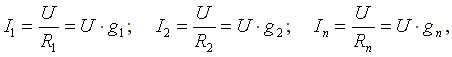
где 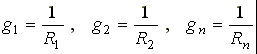- проводимости 1-й, 2-й и n-й ветвей.

В соответствии с первым законом Кирхгофа, ток в неразветвленной части схемы равен сумме токов в параллельных ветвях.

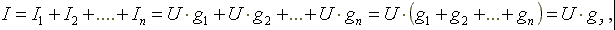
где

Эквивалентная проводимость электрической цепи, состоящей из n параллельно включенных элементов, равна сумме проводимостей параллельно включенных элементов.
Эквивалентным сопротивлением цепи называется величина, обратная эквивалентной проводимости

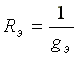
Пусть электрическая схема содержит три параллельно включенных сопротивления.
Эквивалентная проводимость

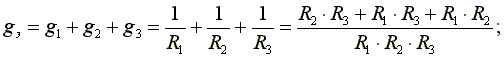
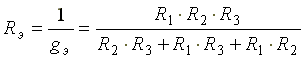
Эквивалентное сопротивление схемы, состоящей из n одинаковых элементов, в n раз меньше сопротивлений R одного элемента

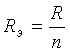
Возьмем схему, состоящую из двух параллельно включенных сопротивлений (рис. 2.3). Известны величины сопротивлений и ток в неразветвленной части схемы. Необходимо определить токи в параллельных ветвях.

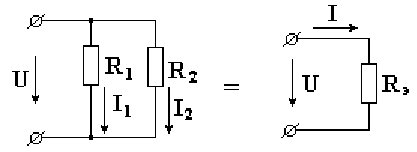
Рис. 2.3 Эквивалентная проводимость схемы

,

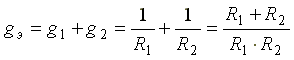а эквивалентное сопротивление

Напряжение на входе схемы

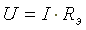Токи в параллельных ветвях

Аналогично

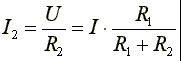
Ток в параллельной ветви равен току в неразветвленной части схемы, умноженному на сопротивление противолежащей, чужой параллельной ветви и деленному на сумму сопротивлений чужой и своей параллельно включенных ветвей.

2.3.Преобразование треугольника сопротивлений
в эквивалентную звезду

Встречаются схемы, в которых отсутствуют сопротивления, включенные последовательно или параллельно, например, мостовая схема, изображенная на рис. 2.4. Определить эквивалентное сопротивление этой схемы относительно ветви с источником ЭДС описанными выше методами нельзя. Если треугольник сопротивлений R1-R2-R3, включенных между узлами 1-2-3 заменить трехлучевой звездой сопротивлений, лучи которой расходятся из точки 0 в те же узлы 1-2-3, эквивалентное сопротивление полученной схемы легко определяется.

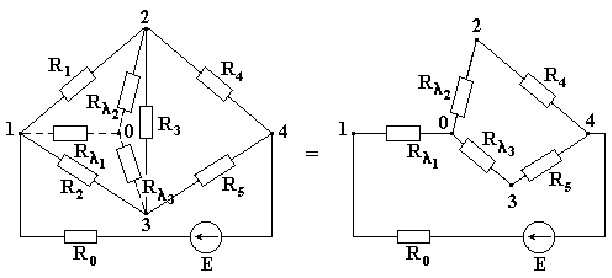
Рис. 2.4 Сопротивление луча эквивалентной звезды сопротивлений равно произведению сопротивлений прилегающих сторон треугольника, деленному на сумму сопротивлений всех сторон треугольника.
В соответствии с указанным правилом, сопротивления лучей звезды определяются по формулам:

Эквивалентное соединение полученной схемы определяется по формуле

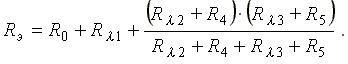
Сопротивления R0 и Rλ1 включены последовательно, а ветви с сопротивлениями Rλ1 + R4 и Rλ3 + R5 соединены параллельно.

2.4.Преобразование звезды сопротивлений
в эквивалентный треугольник

Иногда для упрощения схемы полезно преобразовать звезду сопротивлений в эквивалентный треугольник.
Рассмотрим схему на рис. 2.5. Заменим звезду сопротивлений R1-R2-R3 эквивалентным треугольником сопротивлений RΔ1-RΔ2-RΔ3, включенных между узлами 1-2-3.

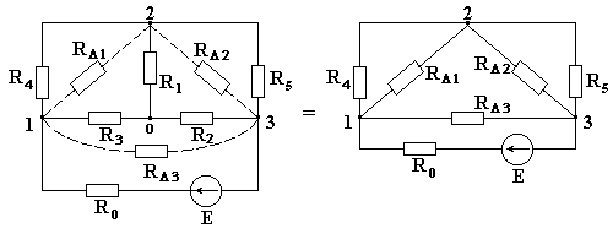
2.5. Преобразование звезды сопротивлений
в эквивалентный треугольник

Сопротивление стороны эквивалентного треугольника сопротивлений равно сумме сопротивлений двух прилегающих лучей звезды плюс произведение этих же сопротивлений, деленное на сопротивление оставшегося (противолежащего) луча. Сопротивления сторон треугольника определяются по формулам:

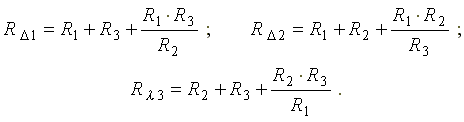
Эквивалентное сопротивление преобразованной схемы равно

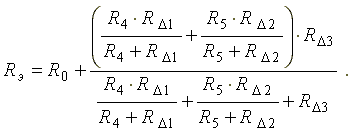
УРОК №16

Date: 2016-05-25; view: 1029; Нарушение авторских прав