Метод комплексных амплитуд. Ограничения на его применение

Установившиеся значения токов и напряжении линейной цепи, находящейся под гармоническим воздействием, могут быть найдены путем непосредственного решения дифференциального уравнения цепи (2.6) при , однако даже для относительно простых цепей эта задача оказывается весьма трудоемкой. На практике анализ таких цепей обычно выполняют с помощью метода комплексных амплитуд, разработанного в конце прошлого века американскими инженерами Ч. П. Штейнметцем и А. Е. Кеннели. Метод комплексных амплитуд, подобно известному логарифмическому методу, основан на идее функционального преобразования, при котором операции над исходными функциями (оригиналами) заменяются более простыми операциями над некоторыми новыми функциями, так называемыми изображениями или символами исходных функций. Методы такого типа называются символическими. Независимо от типа используемых функциональных преобразований решение любой задачи символическими методами содержит, как правило, следующие основные этапы:

прямое преобразование, в результате которого осуществляется переход от исходных величин (оригиналов) к их символам (изображениям);

определение изображений искомых величин путем выполнения по специально установленным правилам операций над изображениями;

обратное преобразование, с помощью которого переходят от изображений к оригиналам.

Каждой гармонической функции времени можно поставить в соответствие комплексное число , называемое мгновенным или текущим комплексом гармонической функции: (2.7)

модуль которого равен амплитуде гармонической функции , а аргумент – её фазе . Как видно из выражения (2.7), вещественная часть мгновенного комплекса равна исходной гармонической функции Геометрически мгновенный комплекс может быть представлен в виде вектора , длина которого в определенном масштабе равна амплитуде соответствующей гармонической функции, а аргумент изменяется во времени по такому же закону, как и фаза гармонической функции . Для того чтобы обеспечить этот закон изменения аргумента, вектор должен вращаться в комплексной плоскости против часовой стрелки с угловой скоростью (рис. 2.1,). В момент времени вектор должен образовывать с положительным направлением вещественной оси угол , равный начальной фазе рассматриваемой гармонической функции. Как видно из рис. 2.1, проекция вектора на вещественную ось в выбранном масштабе времени равна мгновенному значению исходной гармонической функции времени .

Значение мгновенного комплекса в момент времени называется комплексной амплитудой 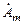гармонической функции времени : (2.8)

Из выражения (2.8) следует, что комплексная амплитуда гармонической функции времени представляет собой комплексное число, модуль которого равен амплитуде рассматриваемой функции, а аргумент – ее начальной фазе . Геометрически комплексная амплитуда мажет быть представлена в виде неподвижного вектора, расположенного под углом к вещественной оси, длина которого в определенном масштабе равна .

Используя понятие комплексной амплитуды, выражение (2.7) для мгновенного комплекса может быть преобразовано к следующему виду: 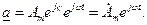(2.9)

Вектор , называемый оператором вращения, имеет единичную длину и вращается в комплексной плоскости против часовой стрелки с угловой скоростью . Всякий неподвижный вектор, будучи умноженным на оператор вращения , начинает вращаться в комплексной плоскости против часовой стрелки с угловой скоростью

комплексное действующее значение гармонической функции представляет собой комплексное число, модуль которого равен действующему значению гармонической функции, а аргумент – её начальной фазе : 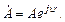(2.10)

Используя выражения и (2.9), можно установить связь между комплексной амплитудой 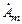гармонической функции и ее комплексным действующим значением :