Вращение абсолютно твердого тела

Если хотя бы две точки абсолютно твердого тела при его вращении остаются неподвижными, то такое вращение называется вращением тела вокруг неподвижной оси. Все точки, лежащие на этой оси и принадлежащие телу также будут неподвижными.

Каждая точка вращающегося твердого тела, не принадлежащая оси, движется по окружности, центр которой находится на оси вращения.

Угол, на который поворачивается каждая точка тела, не лежащая на оси, называется углом поворота. Поэтому угол поворота j аналогичен угловому перемещению точки (рис. 2.8.1).

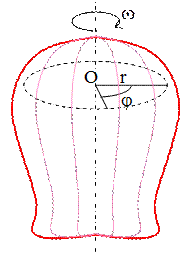
Рис. 2.8.1. Рис. 2.8.2.

Так же как и для движения материальной точки по окружности вводятся определения и соответствующие им формулы угловой скорости w и углового ускорения e (см. 2.6.3 и 2.6.12). Скорость любой точки вращающегося тела, находящейся на расстоянии r от оси вычисляется по формуле: 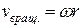. Ускорение произвольной точки тела выражается как сумма нормального и тангенциального ускорений: a = a _n + a _t.

Механическое движение абсолютно твердого тела, при котором только одна из его точек остается неподвижной, называется вращением тела вокруг неподвижной точки.

Ось вращения, проходящая через неподвижную точку перпендикулярно плоскости вращения, называется мгновенной осью вращения.

В качестве примера такого вращения рассмотрим качение колеса без проскальзывания (см. рис. 2.8.2).

Качение без проскальзывания означает, что за время D t, за которое центр колеса смещается на расстояние D s, любая точка обода колеса описывает дугу, длина которой равна D s.

Докажем, что при качении без проскальзывания скорость вращательного движения любой точки колеса равна скорости поступательного движения центра колеса:

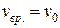. (2.8.1)

Доказательство.

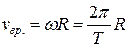, где T – период вращения колеса, R – его радиус. При равномерном движении колеса его центр за время t = T пройдет путь 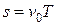. По определению качения без проскальзывания 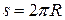, Тогда 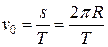, Þ .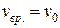

Скорость произвольной точки M, находящейся на ободе колеса, относительно земли равна

v_M = v₀ + v _{вр .}. (2.8.2)

Например, скорость верхней точки A колеса равна v_A = 2v₀, а скорость нижней точки v_O¢ = 0. Поэтому O¢ - неподвижная точка колеса, а значит, через точку O¢ проходит мгновенная ось вращения. Тогда скорость точки M можно также посчитать по формуле:

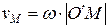, (2.8.3)

где 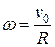, так как колесо движется без проскальзывания.

Date: 2015-05-19; view: 701; Нарушение авторских прав