
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Примеры решения задач на уравнение Клапейрона – Менделеева
З а д а ч а1. Резиновый мяч содержит 4 л воздуха, находящегося при температуре 20 єС при атмосферном давлении 780 мм рт. ст. Какой объем займет воздух, если мяч будет опущен в воду на глубину 10 м? Температура воды 4 єС.
А н а л и з у с л о в и я з а д а ч и: по условию задачи рассматривается воздух в двух состояниях: на поверхности воды и на глубине h. Обозначим параметры состояния в каждом случае.
Решение:
Запишем уравнения состояния для каждого случая, учитывая, что масса воздуха в шаре остается постоянной. Получим систему уравнений
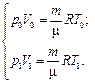
Разделим второе уравнение на первое и выразим искомый объем
Д а н о:
V 0 = 4 л = 4 • 10-3 м3
T 0 = (20 + 273) K
h рт = 780 мм рт. ст.
h в = 10 м
T 1 = (4 + 273) K
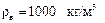
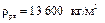 V 1 =?
V 1 =?
| 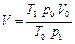 В воде на глубине h давление будет складываться из атмосферного у поверхности воды и давления столба воды высотой h
В воде на глубине h давление будет складываться из атмосферного у поверхности воды и давления столба воды высотой h 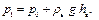 Получим формулу для объема Получим формулу для объема 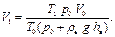 Атмосферное давление дано по условию в мм рт. ст. Для перевода его в паскали записываем формулу Атмосферное давление дано по условию в мм рт. ст. Для перевода его в паскали записываем формулу 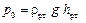 . Окончательная формула . Окончательная формула
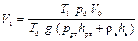 Вычисления дают результат
V 1 = 1,96л.
Вычисления дают результат
V 1 = 1,96л.
|
О т в е т: V 1 = 1,96 л.
З а д а ч а 2. Идеальный газ находится в цилиндрическом сосуде под поршнем. Поместив на поршень груз массой m, его объем изотермически уменьшили в n раз. Какой массы груз следует добавить, чтобы объем газа изотермически уменьшили еще в k раз?
А н а л и з з а д а ч и: По условию задачи рассматриваются три состояния газа. Введем обозначения параметров:
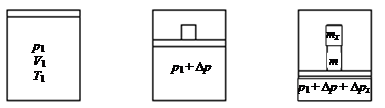
1 2 3
V 1/ n, T 1 V 1/ nk, T 1
Рис. 8
| Д а н о: | Р е ш е н и е |
Т = const
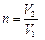
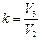 m x =?
m x =?
| Запишем уравнения Бойля - Мариотта для перехода из 1-го состояния во 2-е и для перехода из 1-го состояния в 3-е. Получим систему:
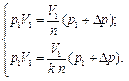 Давление газа увеличивается с давления p 1 в 1-м состоянии благодаря воздействию груза. На газ действует вес груза. Изменение давления, вызванное действием груза во 2-м состоянии, может быть вычислено по формуле
Давление газа увеличивается с давления p 1 в 1-м состоянии благодаря воздействию груза. На газ действует вес груза. Изменение давления, вызванное действием груза во 2-м состоянии, может быть вычислено по формуле
|
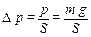 ,
,
где S - площадь поршня.
Тогда давление со стороны груза в 3-м состоянии 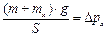 . Подставляя значения изменений давления в систему, сокращая обе части уравнений на V 1, получаем:
. Подставляя значения изменений давления в систему, сокращая обе части уравнений на V 1, получаем:
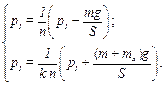
Раскрываем скобки, переносим выражения, содержащие p 1, в левую часть системы:
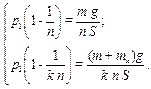
Делим 1-е уравнение на 2-е:
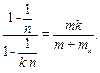
Преобразуем левую часть уравнения:
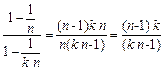 .
.
Получаем уравнение
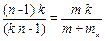 .
.
Делим обе части уравнения на k, используем свойство пропорции, переносим выражения, содержащие неизвестные, в левую часть, а все остальные – в правую. Получаем
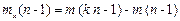 .
.
Окончательная формула: 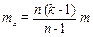 .
.
О т в е т: 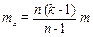 .
.
З а д а ч а 3. Два сосуда с объемами V 1 = 40 л и V 2 = 20 л содержат газ при одинаковой температуре, но разных давлениях. После соединения сосудов в них устанавливается давление р = 1 МПа. Каково начальное давление р 1 в большем сосуде, если в меньшем оно было равно р 2 = 600 кПа? Температура не изменяется.
А н а л и з у с л о в и я з а д а ч и. Процесс соединения сосудов с газом - изотермический. Обозначим параметры состояний. Рассматриваются три состояния. Используется один и тот же газ, молярная масса в обоих сосудах одинаковая, а массы – разные.
1-е состояние 2-е состояние 3-е состояние
параметры V 1 p 1 T V 2 p 2 T (V 1+ V 2) p T
состояния
m 1, µ m 2, µ (m 1 + m 2), µ
| Д а н о: | Р е ш е н и е |
V 1 = 40 л = 4•10-2 м3
V 2 = 20 л = 4•10-2 м3  р = 1 МПа
р = 1 МПа
| Записываем уравнение Менделеева - Клапейрона для каждого состояния. Получаем систему: 
|
| р 2 = 600 кПа T = const p 1 =? |    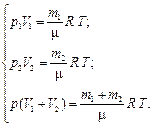
|
Выразим из первых двух уравнений массы и подставим их значения в третье уравнение:
p (V 1 + V 2) = 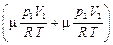
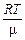 .
.
Преобразуя это выражение, получаем:
p (V 1 + V 2) = p 1 V 1 + p 2 V 2 ,
откуда
р 1 = 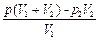 .
. 
О т в е т: р 1 = 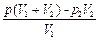 .
.
Date: 2015-05-09; view: 8263; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |