Геометрический смысл определенного интеграла. Выражение площади криволинейной трапеции интегралом

Вычисление площади фигуры является одной из наиболее не простых проблем теории площадей. В школьном курсе геометрии мы научились находить площади основных геометрических фигур, например, круга, треугольника, ромба и т.п. Однако намного чаще приходится сталкиваться с вычислением площадей более сложных фигур. При решении подобных задач приходится прибегать к интегральному исчислению.

В этой статье мы рассмотрим задачу о вычислении площади криволинейной трапеции, причем подойдем к ней в геометрическом смысле. Это позволит нам выяснить прямую связь между определенным интегралом и площадью криволинейной трапеции.

Пусть функция y = f(x) непрерывна на отрезке [a; b] и не меняет знак на нем (то есть, неотрицательная или неположительная). Фигуру G, ограниченную линиями y = f(x), y = 0, x = a и x = b, называют криволинейной трапецией. Обозначим ее площадь S(G).

Подойдем к задаче вычисления площади криволинейной трапеции следующим образом. В разделе квадрируемые фигуры мы выяснили, что криволинейная трапеция является квадрируемой фигурой. Если разбить отрезок [a; b] на n частей 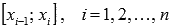точками и обозначить 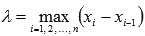, а точки 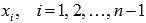выбирать так, чтобы 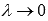при , то фигуры, соответствующие нижней и верхней суммам Дарбу, можно считать входящей P и объемлющей Q многоугольными фигурами для G.

Таким образом, и при увеличении количества точек разбиения n, мы придем к неравенству , где - сколь угодно малое положительное число, а s и S – нижняя и верхняя суммы Дарбу для данного разбиения отрезка [a; b]. В другой записи 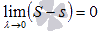. Следовательно, обратившись к понятию определенного интеграла Дарбу, получаем .

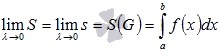Последнее равенство означает, что определенный интеграл для непрерывной и неотрицательной функции y = f(x) представляет собой в геометрическом смысле площадь соответствующей криволинейной трапеции. В этом и состоит геометрический смысл определенного интеграла.

То есть, вычислив определенный интеграл , мы найдем площадь фигуры, ограниченной линиями y = f(x), y = 0, x = a и x = b.

Date: 2015-06-08; view: 631; Нарушение авторских прав